
- •1, Визначники другого і третього порядку, їх властивості.
- •3, Вектором называется направеный отрезок, тоесть отрезок имеющий определенную длину и определенное направление.
- •Свойства векторного произведения
- •9, Мішаний добуток векторів, його обчислення і властивості. Геометричний зміст мішаного добутку. Необхідні і достатні умови компланарності трьох векторів.
- •Свойства смешанного произведения
Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b )•с=(b х с)•а=(с х а)•b .
Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер
2. Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb )•с=а*(bx с).
Действительно, (ахb )•с=±V и а•(b хс)=(b хс)•а=±V . Знак в правой части этих равенств берем один и тот же, так как тройки векторов а , b , с и b , с , а — одной ориентации.
Следовательно, (a хb )•с=a (b хс). Это позволяет записывать смешанное произведение векторов (а х b )с в виде abc без знаков векторного, скалярного умножения.
3. Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb , abc =-bac , abc =-cba .
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
4.Смешанное произведение ненулевых векторов а, b и с равно нулю огда и только тогда, когда они компланарны.
Если abc =0 , то а, b и с— компланарны.
Допустим, что это не так. Можно было бы построить параллелепипед с объемом V¹ 0. Но так как abc =±V , то получили бы, что abc¹0 . Это противоречит условию: abc =0.
Обратно, пусть векторы а, b , с — компланарны. Тогда вектор d =ахb будет перпендикулярен плоскости, в которой лежат векторы а, b ,с, и следовательно, d ^с. Поэтому d •с=0, т. е. abc =0.
Выражение смешанного произведения через координаты
Пусть заданы векторы a =ахi +ayj +azk , b =bxi +byj +bzk , с=cxi +cyj +czk . Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
Полученную формулу можно записать короче:
так как правая часть равенства (8.1) представляет собой разложение определителя третьего порядка по элементам третьей строки.
Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
Некоторые приложения смешанного произведения
Определение взаимной ориентации векторов в пространстве
Определение взаимной ориентации векторов а, b и с основано на следующих соображениях. Если abc > 0 , то а , b , с — правая тройка; если abc <0 , то а, b , с - левая тройка.
Установление компланарности векторов
Векторы а, b и с компланарны тогда и только тогда, когда их смешанное произведение равно нулю
Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на векторах а, b и с вычисляется как V =|аbс|, а объем треугольной пирамиды, построенной на этих же векторах, равен V =1/6*|abc |.
10, Уравнение плоскости, проходящей через точку ( х0 , у 0 , z 0 ) и перпендикулярной вектору ( А, В, C ) :
А ( х – х0 ) + В ( у – у 0 ) + С ( z – z 0 ) = 0 .
Общее уравнение плоскости:
Ах + Ву + Сz + D = 0 ,
где А, B и C не равны нулю одновременно.
Коэффициенты А, B и C являются координатами нормального вектора плоскости ( т.е. вектора, перпендикулярного плоскости ).
11, Нормальным уравнением плоскости называется ее уравнение, написанное в виде
![]() ,
(1)
,
(1)
где
![]() ,
,
![]() ,
,
![]() -
направляющие косинусы нормали плоскоти,
p - расстояние от начала координат до
плоскости. При вычислении направляющих
косинусов нормали следует считать, что
она направлена от начала координат к
плоскости (если же плоскость проходит
через начало координат, то выбор
положительного направления нормали
безразличен).
-
направляющие косинусы нормали плоскоти,
p - расстояние от начала координат до
плоскости. При вычислении направляющих
косинусов нормали следует считать, что
она направлена от начала координат к
плоскости (если же плоскость проходит
через начало координат, то выбор
положительного направления нормали
безразличен).
Пусть
![]() -
какая угодно точка пространства, d -
расстояние от нее до данной плоскости.
Отклонением
-
какая угодно точка пространства, d -
расстояние от нее до данной плоскости.
Отклонением
![]() точки
от
данной плоскости называется число +d,
если точка
и
начало координат лежат по разные стороны
от данной плоскости, и число -d, если они
лежат по одну сторону от данной плоскости
(если
лежит
на самой плоскости, то отклонение равно
нулю).
точки
от
данной плоскости называется число +d,
если точка
и
начало координат лежат по разные стороны
от данной плоскости, и число -d, если они
лежат по одну сторону от данной плоскости
(если
лежит
на самой плоскости, то отклонение равно
нулю).
Если
точка
имеет
координаты
![]() ,
,
![]() ,
,
![]() ,
а плоскость задана нормальным уравнением
,
а плоскость задана нормальным уравнением
,
то отклонение точки от этой плоскости дается формулой
![]() .
.
Очевидно,
![]() .
.
Общее уравнение плоскости
![]()
приводится к нормальному виду (1) умножением на нормирущий множитель, определяемый формулой
![]() ;
;
знак нормирующего множителя берется противоположным знаку свободного члена нормируемого уравнения.
Уравнение плоскости, проходящей через три заданные точки
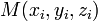 ,
не
лежащие на одной прямой:
,
не
лежащие на одной прямой:
![]()
(смешанное произведение векторов), иначе
![]()
Уравнение плоскости в отрезках:
![]()
где
![]() ,
,
![]() ,
,
![]() —
отрезки,
отсекаемые плоскостью на осях
—
отрезки,
отсекаемые плоскостью на осях
![]() и
и
![]() .
.
12,
Векторне,
канонічне, параметричне рівняння прямої
в просторі. Векторне:
![]()
Параметричне:
![]()
Канонічне:
![]()
Рівняння
прямої що проходить через дві задані
точки:
![]()
![]()
Загальне
рівняння прямої в просторі:
![]()
![]()
![]()
![]()
![]()
Приведем уравнение (4) к каноническому уравнению.
Найдем т. М0-?
Пусть х – свободное неизвестное, х=х0
![]()
![]() Получим
систему 2-х уравнений с двумя неизвестными
(*). y, z – основные неизвестные. Решаем
систему (*) любым способом, например
методом Крамера.
Получим
систему 2-х уравнений с двумя неизвестными
(*). y, z – основные неизвестные. Решаем
систему (*) любым способом, например
методом Крамера.
![]()
Так как Δ≠0, то система (*) имеет единственное решение.
Найдем вектор
 -?
-?

![]()


![]()
13, Різні види рівнянь прямої на площині.
Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
Уравнение прямой по точке и вектору нормали
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой, проходящей через эти точки:
![]()
уравнением прямой с угловым коэффициентом k: y=kx+b
14, Расстояние от точки до прямой на плоскости
Теорема. Если задана точка М(х0 , у0 ), то расстояние до прямой Ах + Ву + С =0 определяется как
 .
.
Доказательство. Пусть точка М 1(х 1, у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1 :
![]() (1)
(1)
Координаты x1 и у1 могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:
A(x – x 0 ) + B(y – y0 ) + Ax0 + By0 + C = 0,
то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:
Теорема доказана.
Відстань від точки до прямої в просторі.
1
спосіб:

А)
так как расстояние от т. М0
до l есть расстояние от т. М0
до ее проэкции на l, т. М1,
то
![]() ,
переход четер т. М0.
За
,
переход четер т. М0.
За
![]() ,
т.к.
,
т.к.
![]() колинеарны.
колинеарны.
![]() (5).
(5).
Б) Переход т переноса прямой (и П, пол. т. М1 (см (5)).
В) На оХ растет от т. М0 до т. М1 (x1,y1,z1)
![]()
2 способ:

![]()
![]()

Відстань між мимобіжними прямими: Пусть прямая
![]()
![]() .
Две
прямые называются скрещивающимися
прямыми если они не лежат в одной
плоскости.
.
Две
прямые называются скрещивающимися
прямыми если они не лежат в одной
плоскости.
![]()
![]()
![]()
![]() .
Две
прямые l1
и l2
являются
скрещивающимися
.
Две
прямые l1
и l2
являются
скрещивающимися
![]()
15,
Кут
між площинами:
![]()
![]()
![]()
![]() .
Двухгранным
углом между плоскостями П1
и П2
называется линейный угол между их
нормальными векторами.
.
Двухгранным
углом между плоскостями П1
и П2
называется линейный угол между их
нормальными векторами.
![]()
![]() =
= =
=
= =
![]()
А)
![]()
![]()
![]()
![]()
![]()
Б)
![]()
![]()
![]()
![]()
![]()
![]()
Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности
О:
Углом![]() между
двумя прямыми
между
двумя прямыми![]() и
и![]() на
плоскости будем называть наименьший
угол, на который нужно повернуть прямую
на
плоскости будем называть наименьший
угол, на который нужно повернуть прямую![]() в
положительном направлении так, чтобы
она совпала с прямой
в
положительном направлении так, чтобы
она совпала с прямой![]()
Пусть
прямые![]() и
и![]()
заданы уравнениями:
![]()
Из
рис. 3.2 видно, что![]() ,
,

Рис. 3.3
![]() .
Окончательно
.
Окончательно![]() .
.
Прямые![]() и
и![]() параллельны
в том и только том случае, когда
параллельны
в том и только том случае, когда
![]() ,
т.е.
,
т.е.![]() .
В случае перпендикулярности прямых
.
В случае перпендикулярности прямых![]() не
существует, т.е.
не
существует, т.е.![]() .
.
15,
Кут
між прямими в просторі.
![]()

![]()


![]()
![]()
А)
Умова паралельносты l1
і l2:
![]()
Б)
Умова перпендикулярності l1
і l2:
![]()
Кут
між прямою l і прощиною П:
![]()
![]()
![]()
![]()
![]() Кут
між прямою і площиною називається кутом
між цьою прямою і проекцією цьої прямої
на площині.
Кут
між прямою і площиною називається кутом
між цьою прямою і проекцією цьої прямої
на площині.


![]() если
если
![]() ,
,
![]()
![]() если
если
![]()
![]() ,
,
![]()
А)
![]()

![]()
![]()
Б)
![]()

![]()
17, Криві другого порядку. Коло. Еліпс. Ексцентриситет, директриси еліпса, їх властивості.
Кривые второго порядка:
Опр:
Кривой второго порядка называется
множество точек которые удовлетворяют
уравнения второго порядка относительно
х и у вида:
![]()
![]()
Существуют системы координат в которых ур (1) принимает найпростейший канонический вид.
 -окружность
-окружность -эипс
-эипс
 -гипербола
-гипербола
 -
парабола
-
парабола -паралельные
прямые
-паралельные
прямые -точки
(0;0)
-точки
(0;0) ,
,
 - прямые
(оси коорд.)
- прямые
(оси коорд.)
 -
- или
или

Уравнение (1) может представлять кривую второго порядка, а может ее и не представлять. Поэтому кривых второго порядка всего 4, и они все выражаются уравнением (1), наоборот – неверно.
Окружность:
Опр: окружностю наз геом. Место точек плоскости равноудаленных от одной заданой точки называемой центром.
Выведим
уравнение окружности исходя из ее
определения.
![]()
![]()
Элипс:
Опр: элипсом наз, множество всех точек плоскости сумма расстояния от которых до двух заданых точек плоскости фокусов есть величина постоянная и большая чем расстояние между фокусом. Расстоянием ПДСК так чтобы оХ проходила через фокус а т. О делит расстояние между фокусом пополам.

![]()
![]() -фокальное
расстояние,
-фокальное
расстояние,
![]() -фокусы
элипса,
-фокусы
элипса,
![]() ,
а-постоянная величина. Т. М принадлежит
элипсу
,
а-постоянная величина. Т. М принадлежит
элипсу
![]() .
Выведим каноническое уравнение элипса
исходя из определения:
.
Выведим каноническое уравнение элипса
исходя из определения:
![]() (2).
Преобразовуя формулу (2) прийдем к
каноническому уравнению элипса
(2).
Преобразовуя формулу (2) прийдем к
каноническому уравнению элипса
![]() ,
где
,
где
![]()
![]() .
Это уравнение второй степени относительно
х и у => элипс кривая второго порядка.
.
Это уравнение второй степени относительно
х и у => элипс кривая второго порядка.

![]() .
Если a=b, получаем
.
Если a=b, получаем
![]() - уравнение окружности О(0.0), и радиусом
- уравнение окружности О(0.0), и радиусом
![]() ,
b=a, то с=0 => фокусы окружности совпадают
с его центром. Значит окружность является
частным случаем элипса. Мера отклонения
элипса от окружности характеризуется
величиной Ԑ, которая называется
ексцентриситетом элипса:
,
b=a, то с=0 => фокусы окружности совпадают
с его центром. Значит окружность является
частным случаем элипса. Мера отклонения
элипса от окружности характеризуется
величиной Ԑ, которая называется
ексцентриситетом элипса:
![]() .
- дирекстиса.
.
- дирекстиса.
18,
Гіпербола.
Асимптоти гіперболи. Ексцентриситет,
директриси гіперболи, їх властивості.



19, Парабола. Директриси парабои, їх властивості. Загальне означення кривої другого порядку.




20, поняття поверхні другого порядку. Циліндричні поверхні.

![]()


21, сфера, еліпсоїд.



22, одно порожнинний гіперболоїд. Двопорожнинний гіперболоїд.
![]()
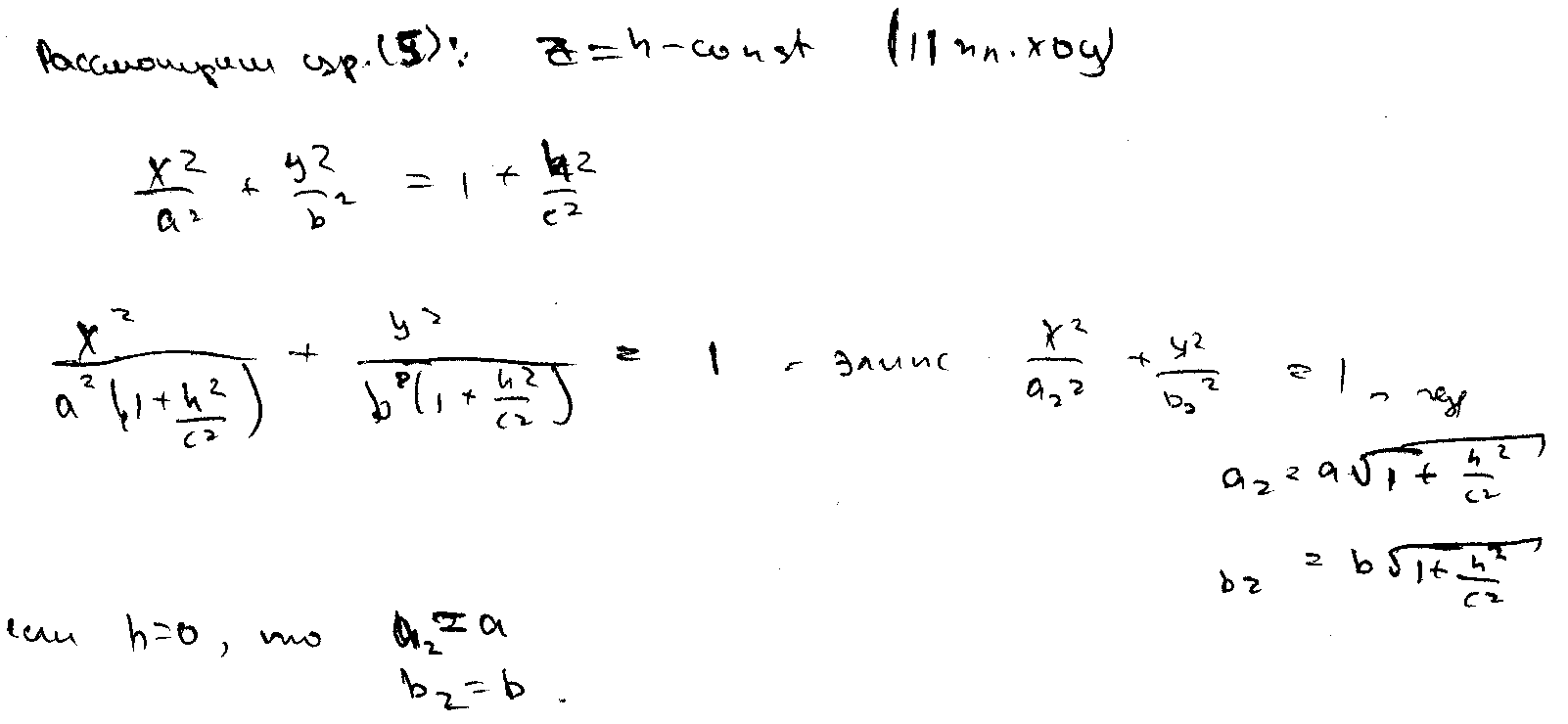



23, еліптичний параболоїд. Гіперболічний параболоїд.
![]()





24, Матриці і дії над ними.




25, Обернена матриця і її застосування.



26, Ранг матриці. Елементарні перетворення матриць. Теорема Кронекера-Капеллі.



