3, Вектором называется направеный отрезок, тоесть отрезок имеющий определенную длину и определенное направление.

Векторы называются равными, если они имеют одинаковые длины, лежат на параллельных прямых или на одной прямой и направлены в одну сторону.

Число, равное длине ветора (при заданном масштабе), называется его модулем. Модуль вектора a обозначается символом или а. Если , то вектор называется единичным.

Единичный вектор, имеющий одинаковое направление с данным вектором , называется ортом вектора и обозначается обычно символом .

Проекцией вектора на ось u называется число, равное величине отрезка оси u, где точка является проекцией точки А на ось u, а - проекцией точки В на эту ось.

Проекция вектора на ось u обозначается символом . Если вектор обозначен символом , то его проекцию на ось u принято обозначать: .

Проекция вектора на ось u выражается через его модуль и угол наклона к оси u формулой

Проекции произвольного вектора на оси некоторой заданной системы координат в дальнейшем обозначаются буквами X, Y, Z. Равенство ={X, Y, Z} означает, что числа X, Y, Z являются проекциями вектора на координатные оси. Вектор, для которого X=Y=Z=0, называется нулевым и обозначается .

Проекции вектора на координатные оси называются также его (декартовыми) координатами. Если даны две точки (M1 (x1,y1,z1) и M2(x2, y2, z2), являющиеся соответственно началом и концом вектора , то его координаты X, Y, Z определяются по формулам , , .

Формула позволяет по координатам вектора определить его модуль.

Линейные операции над векторами:

Сложение векторов. Пусть и – два произвольных вектора. Возьмем произвольную точку О и построим вектор ; затем от точки А отложим вектор . Вектор , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается

Вычитание векторов. Разностью векторов и называется такой вектор , который в сумме с вектором дает вектор : : и

Если векторы и привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому»

Умножение вектора на число. Произведением вектора на действительное число называется вектор (обозначают ), определяемый следующими условиями:

1. ,

2. при и при .

Очевидно, что при .

Построим, например, векторы и для заданного вектора .

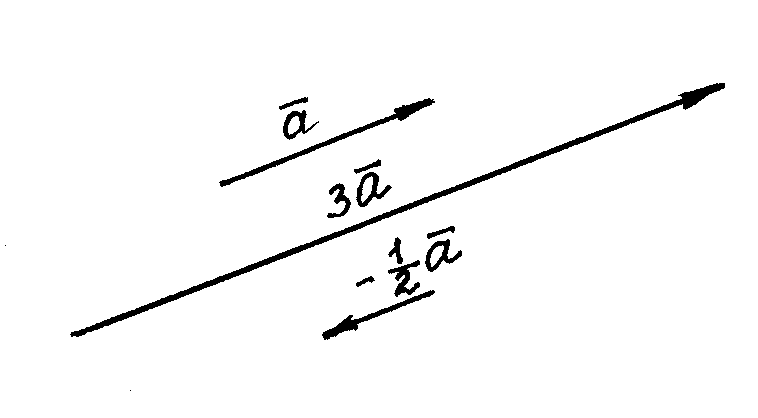
Из определения следует: два вектора и коллинеарны тогда и только тогда, когда имеет место равенство :

Свойства линейных операций:

1. ;

2. ;

3. ; ;

4. ;

5. ;

6. ;

7. ; ;

Пусть дан вектор . Ортом вектора (обозначается ) называется вектор единичной длины, сонаправленный с вектором .

Очевидно, для любого вектора .

4, Вектори в декартовій системі координат. Рассмотрим случай трехмерного пространства (на плоскости все построения аналогичны). Фиксируем некоторую точку и возьмем произвольную точку . Радиус-вектором точки по отношению к точке называется вектор .

Если в пространстве выбран базис, то вектор раскладывается по этому базису. Таким образом точке можно сопоставить упорядоченную тройку чисел -- координаты ее радиус-вектора.

        Определение   Декартовой системой координат в пространстве называется совокупность точки и базиса.        

Точка носит название начала координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат. Первая -- осью абсцисс, вторая -- осью ординат, третья -- осью аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.

        Определение Координаты радиус-вектора точки по отношению к началу координат называются координатами точки в рассматриваемой системе координат.        

Первая координата называется абсциссой, вторая -- ординатой, третья -- аппликатой.

Аналогично определяются декартовы координаты на плоскости. Разумеется, точка на плоскости имеет только две координаты -- абсциссу и ординату.

Координаты точки обычно пишут в скобках после буквы, обозначающей точку, например , .

Направляючі косинуси вектора. Направление вектора в пространстве определяется углами , которые вектор образует с осями координат (рис. 12). Косинусы этих углов называются направляющими косинусами вектора: , , .

Рис. 12

Из свойств проекций: , , . Следовательно,

, , . (2.5)

Легко показать, что

1. ;

координаты любого единичного вектора совпадают с его направляющими косинусами: .

5, Поділ відрізка в заданому відношенні. Говорят, что точка делит отрезок в отношении , если , или (рис. 13).

Рис. 13

Пусть координаты точек и известны: , . Найдем координаты точки . Очевидно, что , где , . Приравнивая координаты векторов, найдем:

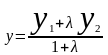, , . (2.6)

В частности, если – середина отрезка , то , тогда

, , . (2.7)

6, Определение скалярного произведения

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.

Обозначается ab,а* b(или( а, b)).Итак, по определению,

 

Формуле   (6.1)   можно   придать   иной   вид.   Так   как | a| cosg=пр _ba, (см. рис.14), a |b| cosg = пр _ab, то получаем:

     

 т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Свойства скалярного произведения

    1. Скалярное произведение обладает переместительным свойством: ab=ba

 

Решение:                                                             

5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a ^b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а¹ 0 ¹b, то а ^ b

.

Выражение скалярного произведения через координаты

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

  

    т.е

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Пример 6.2.

Доказать, что диагонали четырехугольника, заданного координатами вершин А(-4;-4;4), В(-3;2;2),C(2; 5;1), D(3;-2;2), взаимно перпендикулярны.

Решение: Составим вектора АС и BD, лежащие на диагоналях данного четырехугольника. Имеем: АС = (6;9;-3) и BD = (6;-4;0). Найдем скалярное произведение этих векторов:

АС • BD = 36 - 36 - 0 = 0.

Отсюда следует, что AC^BD. Диагонали четырехугольника ABCD взаимно перпендикулярны.

Угол между векторами

    Определение угла φ между ненулевыми векторами а = (a_x; a_y; a_z) и b=( b_х; b_у; b_г):

Отсюда следует условие перпендикулярности ненулевых векторов а и b:

Необходимое и достаточное условие перпендикулярности векторов и имеет вид:

Механический смысл скалярного произведения

Работа A постоянной силы

, действующей на материальнную точку, при ее перемещениин из точки A в точку B определяется формулой

A = (, ).

7, Определение векторного произведения

Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).

     

 Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. с^а и с^b;

2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е.

3.Векторы a, b и с образуют правую тройку.

Векторное произведение обозначается а х b или [а,b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k (см. рис. 18):

i х j = k,    j х k = i,    k х i = j. Докажем, например, что iхj=k.

1) k^i, k^j;

2) |k|=1, но | i x j| = |i| • |J| • sin(90°)=1;

3) векторы i , j и k образуют правую тройку (см. рис. 16).