1, Визначники другого і третього порядку, їх властивості.
Определителем другого і третього порядку наз числа x1y2–y1x2 і x1y2z3+y1z2x3+z1x2y3–z1y2x3–y1x2z3– x1z2y3.
Властивості:
СВОЙСТВО 1. Величина определителя не
изменится, если все его строки заменить
столбцами, причем каждую строку заменить
столбцом с тем же номером, то есть
СВОЙСТВО
2. Перестановка двух столбцов или двух
строк определителя равносильна умножению
его на -1. Например,
СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
СВОЙСТВО
4. Умножение всех элементов одного
столбца или одной строки определителя
на любое число k равносильно умножению
определителя на это число k. Например,
СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).
СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
СВОЙСТВО
7. Если каждый элемент n-го столбца или
n-й строки определителя представляет
собой сумму двух слагаемых, то определитель
может быть представлен в виде суммы
двух определителей, из которых один в
n-м столбце или соответственно в n-й
строке имеет первые из упомянутых
слагаемых, а другой - вторые; элементы,
стоящие на остальных местах, у вех трех
определителей одни и те же. Например,
СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,
Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.
Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.
Алгебраическое
дополнение элемента мы будем обозначать
большой буквой того же наименования и
тем же номером, что и буква, кторой
обозначен сам элемент.
СВОЙСТВО
9. (теорема 1 (теорема о разложении
определителя по строке или столбцу)))
Определитель
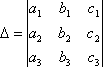равен сумме произведений элементов
какого-либо столбца (или строки) на их
алгебраические дополнения.
СВОЙСТВО 10. (теорема 2(теорема об анулировании определителя)). Сума произведений элементов какой либо строки (столбца) на алгебраическое дополнение другой строки (столбца) равна нулю. Доказательство…
2,
Системой
m линейных уравнений с n неизвестными
называется система вида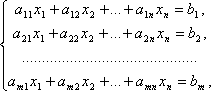
где aij и bi (i=1,…,m; b=1,…,n) – некоторые
известные числа, а x1,…,xn – неизвестные.
В обозначении коэффициентов aij первый
индекс i обозначает номер уравнения, а
второй j – номер неизвестного, при
котором стоит этот коэффициент.
Коэффициенты при неизвестных будем
записывать в виде матрицы
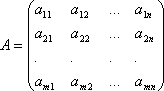, которую назовём матрицей системы.
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
Система может иметь единственное решение.
Система может иметь бесконечное множество решений. Например,
. Решением этой системы является любая
пара чисел, отличающихся знаком.И третий случай, когда система вообще не имеет решения. Например,
,
если бы решение существовало, то x1 + x2
равнялось бы одновременно нулю и
единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Формулы Крамера: .
Однородный
системы уравнений. Рассмотрим m уравнений
с n – неизвестными
(1)
Х1=0, Х2=0, … , Xn=0, так как при подстановке в систему каждое уравнение обращается в тотожность. Определение: Нулевое решение системы называется тривиальным решением.
Теорема 1: Если матрица системы (1 (только вместо m и n написать n n)) имеет определитель не равен нулю, то эта система имеет единственное нулевое решение. Доказательство: из Теоремы Крамера если Δ≠0, => Хi = , i=
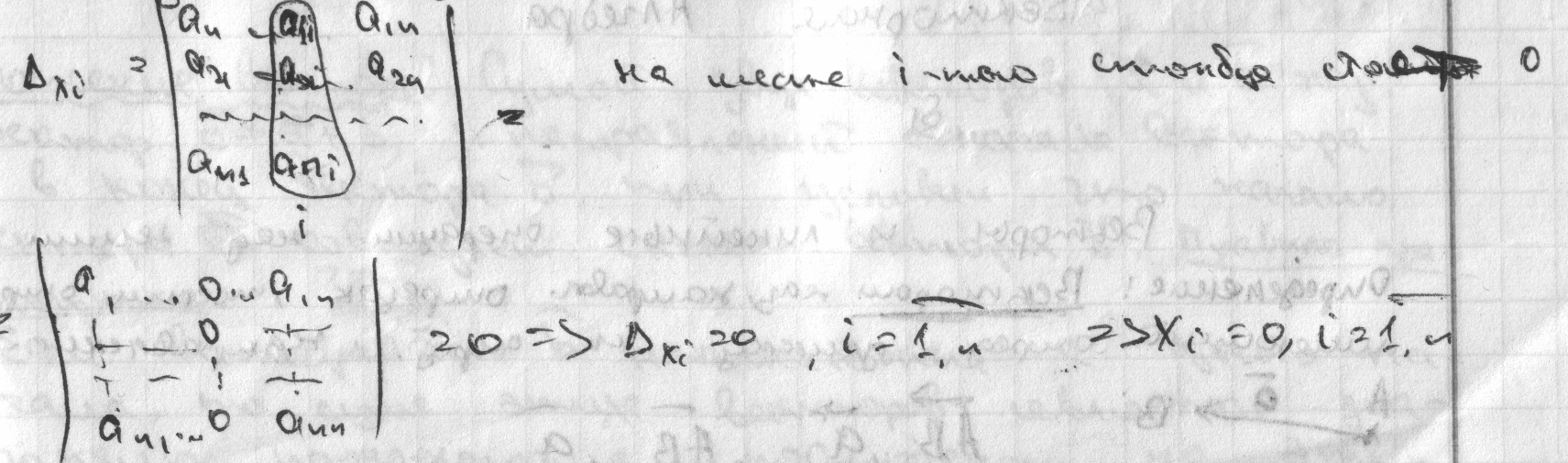
Теорема 2: Если определитель матрицы системы равен 0, то система имеет бессконечное множество решений. Эти решения можно найти методом гаусса.