1. Ряди. Властивості збіжних рядів.

2. Теореми порівняння

3. Ознаки збіжності числових рядів з додатними членами

4. Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди, їх властивості.

5. Функціональні ряди. Властивості рівномірно збіжних рядів

6. Неперервність суми функціонального ряду

7. Почленне інтегрування та диференціювання раціональних рівнянь

8. Степеневі ряди. Теорема Абеля. Радіус збіжності.

9. Почленне дифер. Степ. Рядів. Рівномірна збіжність степеневих рядів.

10. Ряд Тейлора. Ряди Маклорена основних елементарних функцій.

11. Біоміальний ряд.

12. Ряд Фур’є з періодичної функції з періодичної функції.Теор Діріхле.

13. Ряд Фур’є для парних і непарних функцій.

14. Ряди Фур’є з довільним періодом. Ряд Фур’є функції заданої на дов. Проміжку. Теор. Діріхле.

15. Ряд Фур’є в комплексній Формі. Теорема Діріхле.

16. Інтеграл Фур’є в тригонометричній формі. Умови збіжності.

17. Інтеграл Фур’є в в комплексній формі.

18. Перетворення Фур’є в комплексній формі .sin-,cos- перетворення Фур’є

19. Властивості перетворення Фур’є.

20. Похідна ф-ції комплексної змінної. Умови Коші – Рімана.

21. Геометричний зміст модуля.

22. Елементарні функції та їх властивості

23. Елементарні функції sinz;cosz;lnz

24. Обернено тригон.функції та їх властивості.

25. Інтегра від функції комплексної змінної. Його властивості,формула обчислення(довести 4 власт)

26. Інтегральна теорема Коші. Узаг. теорема коші.

27. Інтегр. Ф-ла Коші

28. Первісна функції комплексної змінної(довести самост.)

29. Ряд Тейлора(ФКЗ). Формула Коші для похідної.

30. Ряд Лорана.

31. Особливі точки ФКЗ. Їх класифікація.Ряд Лорана в усувн.т.

32. Ряд Лорана в полюсі.

33. Лишки, їх обчислення. Обчислення лишків в полюсі.

34. Перетв Лапласа.Зображення деяких оригіналів

35. Властивості перетворення Лапласа.

36. Теорема Бареля

37. Формула Рімана – Мелліна.

38. Знаходження оригіналів за допомогою лишків.

39. Ітеграл Дюамеля

1 Ряди. Властивості збіжних рядів.

Означення: Ряд – вираз вигляду a₁+а₂+…+а_n+… . Домовилися ряд позначати скорочено

а_n – загальний член ряду. S_n= a₁+а₂+…+а_n – часткова сума ряду. Означення: Сума ряду – число якщо вона існує, то кажуть що ряд збігається і навпаки. Якщо всі а_n – const, то ряд називають числовим. Якщо а_n – ф-ції, то ряд функціональний.

В ластивості збіжних рядів

Теорема (необхідна ознака збіжності): Якщо ряд збігається то існує. Обернене твердження не вірне, так як умова не є достатньою.

Доведення: ;

S_n-S_n-1=a_n ;

Наслідок: Якщо , то можна стверджувати, що ряд розбігається.

Теорема: Якщо ряд збігається, а сума дорівнює S, то ряд має суму kS.

Доведення: S_n=a₁+a₂+…+a_n; σm=ka₁+ka₂+…+ka_n=kS_n

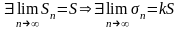
Теорема: , - збігаються і їх суми дорівнюють S та σ → - збігаються, то їх суми дорівнюють S±σ.

Теорема: Якщо ряд збігається (розбігається) і в ньому відкинути скінченну кількість членів, то одержимо збіжний (розбіжний ряд).

Доведення: Ряд , відкинемо k будь-яких членів ряду. Позначимо їх суму через C_k. Розглянемо таке n, щоб всы відк. члени мали номер менше за n. Тоді S_n=C_k+σ_n; .

Висновок: Збіжність не залежить від того з якого n починається відлік.

2 Теореми порівняння

Теорема: Якщо n є N: a_n≤b_n →

1. ∑b_n – збігається → ∑a_n – збігається

2. ∑a_n – розбігається → ∑b_n – розбігається

Коли виконується a_n≤b_n ряд b є мажорант ним до ряду а.

Доведення: Позначимо S_n=a₁+a₂+…+a_n; σ_n=b₁+b₂+…+b_n; S_n ≤σ_n

1. Припустимо ∑b_n – збігається: ; S_n обмежено зверху (S_n≤σ), за теоремою Вейерштрассе значить ∑a_n– збігається

2. Нехай ∑a_n – розбігається → S_n – необмежена, σ_n≥ S_n → - розбігається.

Гранична теорема порівняння: Нехай існує границя

, λ – скінчене число. Тоді ряди , або обидва збігаються, або обидва розбігаються.

Доведення: розглянемо ξ=λ/2>0

За означенням границі, починаючи з деякого номера N усі члени послідовності попадають в проміжок (λ/2;3/2λ); ;

Нехай ∑a_n - збігається, тоді за попередньою теоремою → - збіжний; - збіжний. Нехай ряд ∑a_n – розбіжний, використавши праву частину нерівності, одержимо, що ∑b_n – розбіжний.

3 Ознаки збіжності числових рядів з додатними членами

1. . Перша ознака порівняння.

Нехай маємо ряди та , при цьому для всіх значень виконується нерівність , тоді:

• із збіжності першого ряду випливає збіжність другого ряду.

• із розбіжності другого ряду випливає розбіжність першого ряду.

2. Гранична ознака порівняння.

Нехай для членів рядів та існує скінченна границя , причому . Тоді ці ряди збігаються або розбігаються одночасно.

Доведення: (доведемо, що, якщо другий ряд розбігається, то перший також розбігається):

Для будь-якого знайдеться такий номер починаючи з якого , де . Таким чином 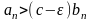. Отже відповідний „хвіст” першого ряду більший за хвіст другого ряду помноженого на . Оскільки відповідно до критерію Коші „хвіст” другого ряду не прямує до нуля, то не прямує до нуля і „хвіст” першого ряду, що свідчить про його розбіжність.

3. Ознака Д’Аламбера.

Якщо для ряду , існує границя , то при - ряд розбіжний; при 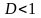- ряд збіжний; при - ряд вимагає дослідження за допомогою інших ознак.

4. Радикальна ознака Коші.

Якщо для ряду існує границя , то при - ряд розбіжний, при - ряд збіжний і при - ряд потребує подальшого дослідження іншим методом.

Доведемо, що ряд збіжний при .

Для будь-якого , існує таке , що при , звідси виходить, що

, що й треба було довести

5. Інтегральна ознака Коші.

Таким чином, якщо ряд збіжний, то збіжним є і невласний інтеграл

Отже, розглянутий вище ряд та невласний інтеграл першого роду збіжні чи розбіжні одночасно.