30. Теоретико-вероятностный метод решения размерных цепей (прямая задача)?

Прямая задача. Допуски составляющих размеров цепи при заданном допуске исходного размера можно рассчитывать четырьмя способами.

При способе равных допусков принимают, что величины TA_j, E_C(A_j) и λ_j - для всех составляющих размеров одинаковы. По заданному допуску ТА_∆ по формуле ( 3 ) определяют средние- допуски Т_CA_j:

.

Найденные значения Т_CА_j и Е_C(А_j) корректируют, учитывая требования конст­рукции и возможность применения процессов изготовления деталей, экономиче­ская точность которых близка к требуемой точности размеров. Правильность ре­шения задачи проверяют по формуле ( 3 ).

При способе назначения допусков одного квалитета расчет в общем аналогичен решению прямой задачи методом полной взаимозаменяемости. При этом сред­нее количество единиц допуска определится по формуле

.

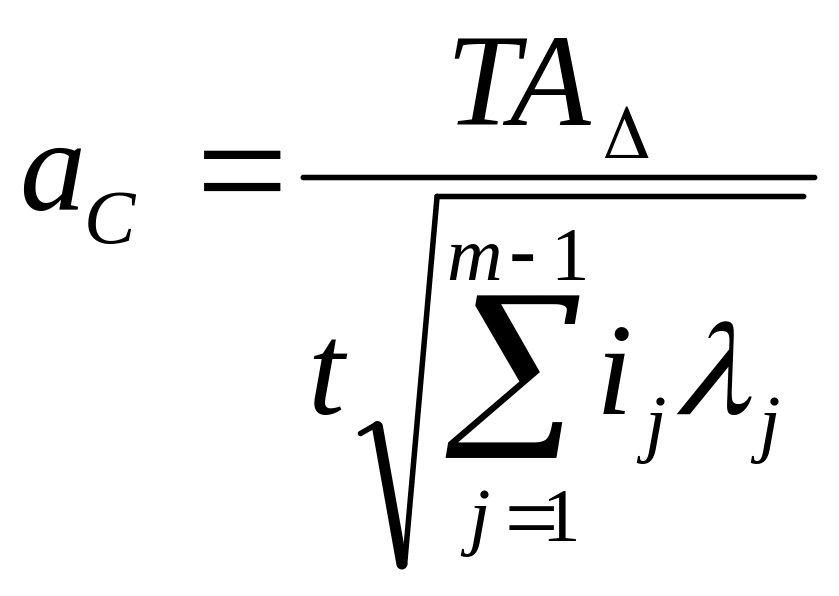Способ пробных расчетов заключается в том, что допуски на составляющие размеры назначают экономически целесообразными для условий предстоящего вида производства с учетом конструктивных требований, опыта эксплуатации имеющихся подобных механизмов и проверенных для данного производства значений коэффициентов λ. Правильность расчета проверяют по формуле ( 3 ).

Способ равного влияния применяют при решении плоских и пространствен­ных размерных цепей. Он основан на том, что допускаемое отклонение каждого составляющего размера должно вызывать одинаковое изменение исходного раз­мера.

31. Теоретико-вероятностный метод решения размерных цепей (обратная задача)?

Обратная задача. В результате совместного влияния систематических и случай­ных погрешностей центр группирования может не совпадать с серединой поля допуска, а зона рассеяния - с величиной допуска. Величина такого несовпаде­ния, выраженная в долях половины допуска на размер, называется коэффициен­том асимметрии:

^,

где М(А_сi) - математическое ожидание, средний арифметический размер i - го звена;

А_cj - размер, соответствующий середине поля допуска.

В этом случае уравнение размерной цепи по средним размерам будет иметь вид

_.

Используя теорему о дисперсии , суммы независимых случайных ве­личин, можно записать:

. ( 1 )

Для перехода от средних квадратичних отклонений σ к допускам или полям рас­сеяния используют коэффициент относительного рассеяния λ_i. Он является от­носительным средним квадратичним отклонением и равен (при поле рассеяния _j = T_j )

( 2 )

Для закона нормального распределения ( при T_j = 6σ_j )

;

для закона равной вероятности ( при T_j = σ_j )

;

для закона треугольника (Симпсона) ( при T_j = σ_j )

.

Подставив выражение ( 2 ) в уравнение ( 1 ), получим:

или ( 3 )

где t - коэффициент, зависящий от процента риска.

Определив ТА_∆ по формуле ( 3 ), вычисляют среднее отклонение замыкающего звена как

, ( 4 )

и его предельные отклонения:

; .