Функция, и их свойства и графики:

1) Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной x однозначно определяет значение выражения x2, а значение месяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Часто под термином «функция» понимается числовая функция; то есть функция которая ставит одни числа в соответствие другим. Отчетливое выявление основных свойств, позволяющих достаточно наглядно судить о ее поведении, называют исследованием функции.

В стандартную схему исследования функции обычно включают следующие пункты.

1. Область определения функции.

2. Нули (корни) функции.

3. Промежутки знакопостоянства.

4. Точки экстремума функции.

5. Промежутки возрастания и убывания (монотонность) функции.

6. Наибольшее и наименьшее значения функции.

7. Множество значений функции.

2) Функция, заданная формулой y = ax2 + bx + c , где x и y - переменные, а a, b, c - заданные числа, причем a=0 , называется

квадратичной функцией.

График квадратичной функции - парабола. Если a > 0 , то ветви параболы направлены вверх. Если a < 0 , то ветви параболы направлены вниз.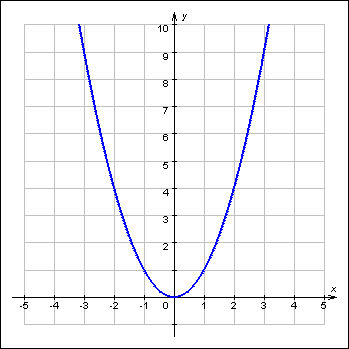

Уравнение и неравенство,

1) Линейным уравнением с одной переменной x называется уравнение вида ax+b=0, где a и b – некоторые числа.

Решить уравнение – значит найти все его корни или доказать, что корней нет. Линейным уравнением называется уравнение вида

ax + b = 0 и любое другое уравнение приводимое к такому виду (например, ax + b = cx + d).

Здесь буквой x(икс) обозначена неизвестная переменная, а буквами a,b - числа. Их называют коэффициентами линейного уравнения:

a - коэффициент при неизвестной,

b - свободный член.

Решить уравнение значит найти такое число(корень уравнения), что при подстановке его вместо переменной x, получается верное равенство.

Примеры линейных уравнений:

2x + 1 = 0. Корень(решение) этого уравнения

− 3x + 1 = x − 7. Корень этого уравнения x = 2

2) Определение.

Квадратным уравнением называют уравнение вида ах+вх+с=0, где х - неизвестное, а, в, с - действительные числа, где: а0.

Родовое понятие - уравнение.

Видовые отличия:

1) имеет вид ах+вх+с=0

(х - неизвестное; а, в, с - действительные числа);

2) а0. Дискриминант

Определение

Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D < 0, корней нет;

Если D = 0, есть ровно один корень;

Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают.

3) Основным методом решения неравенств вида (1) является метод интервалов. Начнём рассматривать его, прежде всего, для многочленов. Этот метод основан на том, что двучлен (x – a) положителен при x > a и отрицателен при x < a, то есть при переходе через точку x = a этот двучлен меняет знак.

Отсюда следуют полезные замечания. Если на интервале (a; b) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.

Пусть функция f непрерывна на интервале I и обращается в нуль в конечном числе точек этого интервала. По сформулированному выше свойству непрерывных функций этими точками I разбивается на интервалы, в каждом из которых непрерывная функция F сохраняет постоянный знак.

Чтобы определить этот знак, достаточно вычислить значение функции f в какой-либо одной точке из каждого такого интервала.