Условие неотрицательности решения
xij 0, (i = ; j = ).
Общая задача линейного программирования
Общей задачей линейного программирования называется задача, которая состоит в определении таких значений неизвестных переменных x1, x2, …, xn, для которых функция цели f(x) = C1 x1 + C2 x2 + …+ Cn xn extremum
принимает экстремальное значение и которые удовлетворяют ограничениям
а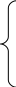
11
x1
+ а12
x2
+…+ а1n
xn
b1,
а21 x1 + а22 x2 + … + а2n xn b2,
…………………………………….
аk1 x1 + аk2 x2 + … + аkn xn bk,
аk+1,1 x1 + аk+1,2 x2 + … + аk+1,n xn = bk+1,
……………………………………..
аm1 x1 + аm2 x2 + … + аmn xmn = bm,
или в более компактном виде
f(x)
=
extremum, (4)
bi;
(i =
),
(5)
=
bi;
(i
=
),
(6)
Хj
0; (j
=
;
S
n),
(7)
где аij, bi, c j - заданные постоянные величины.
Функция (4) называется целевой функцией задачи (4) – (7), а условия (5) – (7) – ограничениями данной задачи.
Совокупность
значений переменных Х1,
Х2,
…, Хn,
удовлетворяющих условиям задачи (5) –
(7), называется допустимым решением, или
планом. План X*
= (
,
,
…
),
при котором целевая функция задачи
принимает экстремальное значение,
называется оптимальным.
Стандартная (симметричная) задача линейного программирования
Стандартной задачей линейного программирования называют задачу, в которой требуется найти такие значения Х1, Х2, …, Хn, при которых функция цели принимает максимальное значение
f(x) = max (8)
и которые удовлетворяют ограничениям
bi; (i = ), (9)
Хj 0; (j = ). (10)
Каноническая (основная) задача линейного программирования
Канонической задачей называется задача, в которой требуется найти такой набор переменных Х1, Х2, …, Хn, который позволяет максимизировать функцию цели
f(x) = max (11)
и удовлетворяет системе ограничений
= bi; (i = ), (12)
Хj 0; (j = ). (13)
Представление задачи линейного программирования в канонической форме
Пусть требуется найти неотрицательные значения переменных Х1, Х2, …, Хn, для которых функция цели принимает максимальное значение
f(x) = C1 Х1 + C2Х2 + …+ CnХn max
при ограничениях
а11Х1
+
а12Х2
+
…+ а1nХn
b1,
а21Х1
+
а22Х2
+
…+ а2nХn
b2, ……………………………….. аm1Х1
+
аm2Х2
+
…+ аmnХn
bm,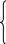
Хj 0, (j = ).
Поскольку в ограничениях левая часть меньше, чем правая (или равна ей), чтобы перейти к строгому равенству, необходимо к левой части каждого неравенства добавить соответствующую переменную.
Найти максимум функции цели
f(x) = C1 Х1 + C2Х2 + …+ CnХn + …+ 0Хn+1 + …+ 0Хn+m max
при ограничениях
а11Х1
+
а12Х2
+
…+ а1nХn
+
Хn+1
=
b1,
а21Х1
+
а22Х2
+
…+ а2nХn
+
Хn+2
=
b2, ………………………………………………. аm1Х1
+
аm2Х2
+
…+ аmnХn
+
Хn+m
=
bm,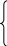
Хj
0, (j
=
).
Пример. Записать следующую задачу в канонической форме:
f(x) = -X1 + 2X2 - X3 + X4 min,
3
X1
- X2
+
2X3
+
2X4
10,
X1 + 2X2 + X3 - X4 8,
2X1 - X2 - X3 + X4 6,
-X1 + 3X2 + 5X3 - 3X4 = 15,
Xj 0, (j = 1 4).
Для записи задачи в канонической форме поменяем знаки у всех коэффициентов функции цели на противоположные. Тогда задача будет заключаться в нахождении максимума целевой функции. Для приведения ограничений – неравенств к системе уравнений необходимо приравнять левые и правые части ограничений путем введения дополнительных переменных. Если левая часть ограничения меньше, чем правая, необходимо добавить дополнительную переменную, если же левая часть ограничения больше, из нее следует вычесть некоторое, пока неизвестное, значение.
f(x) = Х1 - 2Х2 + Х3 - Х4 + 0Х5 + 0Х6 + 0Х7 max,
3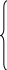
X1
- X2
+
2X3
+
2X4
+
X5
=
10,
X1 + 2X2 + X3 - X4 - X6 = 8,
2X1 - X2 - X3 + X4 + X7 = 6,
-X1 + 3X2 + 5X3 - 3X4 = 15, Xj 0.
Свойства задачи линейного программирования:
1. Множество планов задачи линейного программирования, если оно не пусто, образует выпуклый многогранник. Любая точка внутри области, ограниченной этим многогранником, является допустимым решением задачи.
2. В одной из вершин многогранника решений целевая функция принимает максимальное значение (при условии, что функция ограничена сверху на множестве планов).
3. Если максимальное значение функция принимает более, чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин.