2. Связь между матрицами линейного оператора в различных базисах.

Определение 1. Матрицы A и B называются подобными, если существует такая матрица T, что B = T ^-1 A T.

Теорема 1. Матрицы линейного оператора A векторного пространства V - подобны, т. е. если A и B матрицы линейного оператора  соответственно относительно базисов v = (v₁, v₂, ..., v_n) и u = (u₁, u₂, ..., u_n) векторного пространства V, T- матрица перехода от первого базиса ко второму, то B = T ^-1 A T .

Лемма 1. Пусть v = (v₁, v₂, ..., v_n) - базис векторного пространства V, A и С - матрицы размерности n m. Если vA = vС, то A = С.

Доказательство теоремы. Пусть T = (t_ij) - матрица перехода от первого базиса. По определению матрицы перехода от базиса v к базису u имеем u = vT . По определению матрицы линейного оператора имеем

A(u) = (Au₁, Au₂, ..., Au_n) = (u₁, u₂, ..., u_n)B = uB = (vT)B =v(TB) . (1)

С другой стороны

A(u) == (Au₁, Au₂, ..., Au_n)= (A(t₁₁ v₁ + t₂₁ v₂ + ...+ t_n1 v_n), A( t₁₂ v₁ + t₂₂ v₂ + ...+ t_n2 v_n), ..., A( t_1n v₁ + t_2n v₂ + ...+ t_nn v_n)) =

= (t₁₁Av₁ + t₂₁ Av₂ + ...+ t_n1Av_n, t₁₂Av₁ + t₂₂Av₂ + ...+ t_n2v_n, ..., t_1n Av₁ + t_2nAv₂ + ...+ t_nnAv_n) =

= (Av₁, Av₂, ..., Av_n)T = (v₁, v₂, ..., v_n)AT = vAT. (2)

Так как левые части равенств (1) и (2) равны, то получаем

v(TB) = vAT. (3)

По лемме следует TB = AT. Так как матрица перехода T от одного базиса векторного пространства невырожденная, то она имеет обратную матрицу T ^-1, то находим B = T ^-1 A T. 

3. Операции над линейными операторами. Пусть A, B - линейные операторы в векторном пространстве V, A, B - соответственно матрицы линейных операторов A, B относительно одного базиса v.

Определение 1. Суммой A + B линейных операторов A и B векторного пространства V называется отображение V в V, определенное для любого вектора, а из V по формуле: (A + B)а = Aа + Bа.

Определение 2. Произведение A числа  на линейный оператор A векторного пространства V называется отображение V в V, определенное для любого вектора, а из V по формуле: (A)а = (Aа).

Определение 3. Произведением AB линейных операторов A и B векторного пространства V называется отображение V в V, определенное для любого вектора, а из V по формуле: (AB)а = A(Bа).

Tеорема 1. 1. Сумма A + B двух линейных операторов A, B векторного пространства V линейный оператор векторного пространства V, и матрица линейного оператора A + B равна A + B.

2. Произведение A числа  на линейный оператор A векторного пространства V линейный оператор векторного пространства V, и матрица линейного оператора A равна A.

3. Произведение AB двух линейных операторов A, B векторного пространства V линейный оператор векторного пространства V, и матрица линейного оператора AB равна AB.

4. Характеристическое уравнение линейного оператора. Пусть V - n - мерное векторное пространство над полем P, v =(v₁, v₂, …, v_n) - базис векторного пространства V, A - линейный оператор в векторном пространстве V, A - матрица линейного оператора A в данном базисе,  - переменная.

Определение 1. Характеристическим уравнением линейного оператора A называется уравнение

,

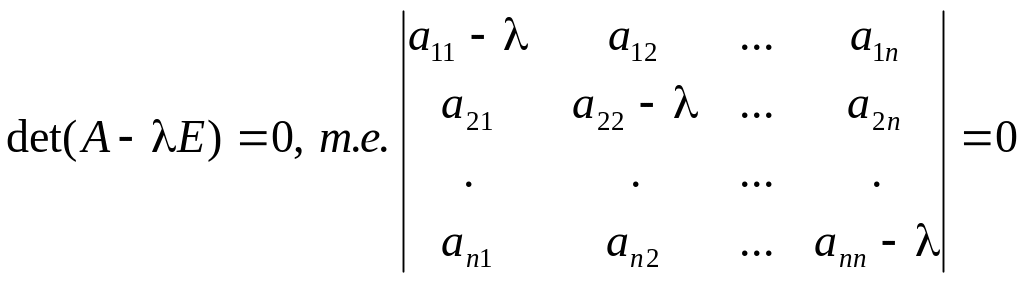Теорема 1. Характеристическое уравнение линейного оператора имеет степень n и не зависит от выбора базиса векторного пространства V.

5. Собственные векторы и собственные значения линейного оператора, и их связь с корнями характеристического уравнения. Пусть A - линейный оператор в векторном пространстве V над полем P.

Определение 1. Ненулевой вектор b называется собственным вектором линейного оператора линейного оператора A, если Ab =  b,  P. Число  называется собственным числом или собственным значением линейного оператора A.

Теорема 1. Число  P является собственным значением линейного оператора A тогда и только тогда, когда  корень характеристического многочлена линейного оператора A.

Собственные векторы линейного оператора A находятся из решения матричного уравнения

где B -координатный столбец собственного вектора b.