0909 Алгебра и геометрия Толстиков а.В. Курс 1. Семестр 1. Лекция 9 (продолжение). Элементы векторной алгебры План

1. Геометрические векторы и операции над ними

2. Базис геометрического векторного пространства

1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 7-22.

2. Ермаков В.И. Общий курс высшей математики. М.: Инфра - М, 2000. с. 72-87

3. Кремер Н.Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 16-26.

4. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1980, с. 148-156.

§ 1. Геометрические векторы

1. Скалярные и векторные величины. Если физическая или ге0метрическая величина характеризуется только одним неотрицательным числом, то она называется скалярной. Например, длина отрезка, площадь фигуры, объем тела, масса тела и т.д. скалярные величины.

Если физическая или геометрическая величина характеризуется не только и численным значением и направлением, то она называется векторной. Например, скорость, ускорение, сила и т.д. векторные величины.

2. Сонаправленность лучей. Любая точка A принадлежащая прямой a делит ее на две части. Лучом называется часть прямой a, расположенная по одну сторону от точки A. Точка A называется началом луча. Если точка B принадлежит лучу, то он обозначается двумя точками AB.

Определение 1. Два луча AB и CD называются сонаправленными, если либо один из лучей содержится в другом луче, либо они лежат на параллельных прямых по одну сторону от прямой AC (см. рис. 1). Обозначаем AB CD. Лучи AB и KL называются противоположно направленными, если луч сонаправлен с лучом дополнительным к лучу KL. Обозначаем AB KL.

Н а рис 1. лучи AB, CD, EF сонаправленные, а лучи AB, KL - противоположно направленные.

Теорема 1. Отношение сонаправленности лучей есть отношение эквивалентности, т.е. для любых лучей AB, CD, EF выполняются свойства:

1. AB CD - рефлексивность,

2. AB CD  CD  AB - симметричность,

3. AB CD & CD  EF  AB  EF - транзитивнсть.

Д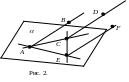 оказательство. Первое и второе свойства, непосредственно следуют из определения сонаправленных лучей. Докажем третье свойство.

Пусть AB CD & CD  EF. Рассмотрим только один случай, когда лучи AB, CD, EF не лежат в одной плоскости (остальные случаи предоставляем рассмотреть самостоятельно).

Из условия следует, что лучи AB, CD, EF лежат на разных параллельных прямых. Тогда точки A, C, E не лежат на одной прямой и рассмотрим плоскость , проходящие через эти три точки, но ни один из лучей не лежит в плоскости (см. рис. 2). Рассмотрим прямые AC, CE, EA, которые лежат в плоскости . Так как AB CD и CD  EF, то лучи AB и CD и лежат по одну сторону от прямой AC и от плоскости , лучи CD и EF лежат по одну сторону от прямой CE и от плоскости . Таким образом лучи AB и EA лежат по одну сторону от плоскости  и поэтому по одну сторону от прямой EA. Следовательно, по определению 1 CD  EF. (убрать)

2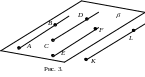 . Лучи AB, CD, EF лежат в одной плоскости , на разных параллельных прямых. Рассмотрим тогда четвертый луч KL, сонаправленный с лучом CD и не лежащий в плоскости . Так как AB CD & CD  KL, то по случаю 1 AB  KL. По свойству 2, KL  CD.Так как KL CD & CD  EF, то по случаю 1 KL  EF. Так как AB KL & KL  EF, то по случаю 1 AB  EF.

Так как отношение сонаправленности лучей является отношением эквивалентности, то множество всех лучей разбивается на классы эквивалентности, каждый из которые состоят из всех лучей сонаправленных друг другу, и называется направлением.

3. Направленные отрезки. Пусть A и B различные точки принадлежащие прямой a. Отрезком AB называется часть прямой a, расположенная между точками A и B. Точка A и B называется концами отрезка AB.

Определение 3. Направленным отрезком называется отрезок AB, обозначаемый символом , у которого один конец A считается первым, а конец В вторым. Первый конец называется началом, а второй - концом направленного отрезка.

На чертеже направленный отрезок изображается стрелкой, идущей из точки A в точку B.

Если конец и начало направленного отрезка совпадают, то он называется нулевым направленным отрезком и изображается на чертеже точкой.

Определение 3. Два направленных отрезка и называются сонаправленными (противоположно направленными), если лучи AB и CD сонаправлены (противоположно направлены), обозначаем символом  (  ).

Определение 4. Длиной или модулем направленного отрезка называется отрезка AB, обозначается символом

Определение 5. Два направленных отрезка и называются равными, если они сонаправлены,  , и их длины равны, = , обозначается символом =

Теорема 2. Отношение равенства направленных отрезков есть отношение эквивалентности, т.е. для любых направленных отрезков , , выполняются свойства:

1. = - рефлексивность,

2. =  = - симметричность,

3. = & =   - транзитивнсть.

Д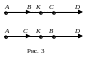 оказательство. Докажем свойство 3, первое и второе свойства доказываются аналогично. По условию = & = . Тогда по определениям 3-5 имеем AB CD, CD  EF и = , = . По теореме 1 и по свойству длины отрезка имеем AB EF и = . Отсюда, по определению,  . 

Имеют место следующие утверждения равносильные определению равенства направленных отрезков.

Теорема 3. Два направленных отрезка и равны тогда и только тогда , когда середины отрезков AD и CB совпадают.

Д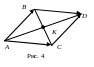 оказательство. Если отрезки , лежат на одной прямой, то утверждение следует из рис. 3. Поэтому рассмотрим случай, когда отрезки AB и CD лежат на разных прямых.

Пусть = . Так как лучи AB и CD сонаправлены, то точки D, B лежат по одну сторону от прямой AC. Так как ABCD, AB= CD, то четырехугольник ADBC - параллелограмм. По свойству диагоналей параллелограмма середины его диагоналей AD и CB совпадают.

Если середины отрезков AD и CB (диагоналей четырехугольника ADBC), совпадают и по признаку четырехугольник ADBC - параллелограмм. Тогда лучи AB и CD сонаправлены и AB = CD. Отсюда по определению 5 = .

Следствие 1. Два направленных отрезка и не лежащие на одной прямой равны тогда и только тогда, когда четырехугольник ADBC - параллелограмм.

Следствие 2. Два направленных отрезка и не лежащие на одной прямой равны тогда и только тогда, когда равны направленные отрезки и .

Доказательство. Утверждения = и = равносильны, так как по теореме 3 оба они равносильны одному и тому же утверждению: середины отрезков AD и CB совпадают. 

4. Определение геометрического вектора. Так как отношение равенства направленных отрезков отношением эквивалентности, то множество всех направленных отрезков разбивается на классы эквивалентности, каждый из которые состоят из всех направленных отрезков равных друг другу.

Определение 6. Вектором, определяемым направленным отрезком называется класс эквивалентности этого направленного отрезка, по отношению равенства направленных отрезков, т.е. вектор это множество всех направленных отрезков, равных . Направленный отрезок называется представителем или изображением вектора.

Вектора будем обозначать строчными жирными буквами a, b и c или строчными буквами со стрелками вверху: , или направленным отрезком принадлежащим вектору. Сам направленный отрезок будем называть также вектором и писать a = .

По свойствам классов эквивалентности, два вектора a и b равны тогда и только тогда, когда равны, изображающие их направленные отрезки.

Длиной или модулем вектора называем длину изображающего его направленного отрезка.

Теорема 4. От любой точки С можно отложить направленный отрезок , который изображает данный вектор a и при этом единственным образом.

Д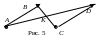 оказательство. Пусть a = . Разделим отрезок BC точкой K пополам. Проведем прямую CK. От K точки на луче, противоположном лучу CK отложим отрезок КD, равный отрезку . Получим точку D. Тогда по теореме 3 направленный отрезок = . Единственность докажите самостоятельно. 

В силу теоремы 4 векторы, которые мы изучаем в геометрии, называются свободными векторами.

Определение 7. Вектор, который изображается нулевым направленным отрезком, называется нулевым, и изображается символом 0.

Таким образом, по определению 0 = .

Определение 8. Два вектора a и b, которые изображаются направленными отрезками, лежащими на одной или на параллельных прямых называются коллинеарными. Обозначаем символом a  b (см. рис. 6).

Определение 9. Два вектора a и b, называются сонаправленными (противоположно направленными), если направленные отрезки, которыми изображаютс эти вектора, сонаправлены (противоположно направлены. Обозначаем символом a  b (a  b) (см. рис. 6).

О пределение 10. Вектора b, называются противоположным вектору a, если они противоположно направлены и имеют одинаковую длину, т.е. a  b и a  =  b . Обозначаем символом b = -a (см. рис. 7).

Определение 10. Три вектора a, b, c, изображаемые направленными отрезками прямых параллельных одной плоскости, называются компланарным (см. рис 7).