
- •0909 Алгебра и геометрия Толстиков а.В. Курс 1. Семестр 1. Лекция 9 (продолжение). Элементы векторной алгебры План
- •§ 1. Геометрические векторы
- •Операция сложения векторов и ее свойства.
- •Вычитание векторов.
- •7. Операция умножения вектора на число и ее свойства.
- •2. Базис векторного геометрического пространства
2. Базис векторного геометрического пространства
1. Базис векторов прямой. Множество V1 векторов фиксированной прямой образует векторное пространство.
Теорема 1. Любой ненулевой вектор e прямой образует базис векторного пространства V1.
Доказательство. По свойству 3 § 2 вектор e образует линейно независимую систему. Пусть a V1. Тогда по свойству линейной зависимости вектор a линейно выражается через вектор e. По определению 1 вектор e образует базис пространства V1.
Теорема 2. Векторы a и b коллинеарны тогда только тогда, когда они линейно зависимы.
Доказательство. Пусть вектора a и b коллинеарны. Если a = 0, то по свойству 3 § 3 вектора a, b линейно зависимы. Если a 0, по теореме о линейной зависимости систем векторов вектор b линейно выражается через вектор a, и векторы a, b линейно зависимы.
Обратно, если векторы a, b линейно зависимы, то по свойству 1 § 3, один из этих векторов линейно выражается через другой и вектора a и b коллинеарны.
Следствие 1. Векторы a и b коллинеарны тогда только тогда, когда они линейно зависимы.
Векторы a и b неколлинеарны тогда только тогда, когда они линейно независимы.
В силу предложений, полученных в предыдущем параграфе, получаем следующие следствия.
Следствие 2. Векторы a = (1, 2,... ,n), b = (1, 2,... ,n) неколлинеарны тогда только тогда, когда ранг матрицы
![]() ,
(12)
,
(12)
составленной из координат векторов, равен 2. Векторы a и b коллинеарны тогда и только когда ранг матрицы (12) равен 1.
Ранг матрицы (12) равен 1 тогда и только тогда, одна из строк матрицы получается из другой строки, умножением на одно и то же число. Поэтому получаем еще следующее утверждение.
Следствие 2. Векторы a = (1, 2,... ,n), b = (1, 2,... ,n) неколлинеарны тогда только тогда, когда координаты векторов соответственно пропорциональны, т.е.
![]() ,
(13)
,
(13)
г де
предполагается, что числитель равен
нулю, если знаменатель равен нулю.
де
предполагается, что числитель равен
нулю, если знаменатель равен нулю.
Базис векторов на плоскости. Множество V2 векторов фиксированной плоскости образует векторное пространство.
Теорема 3. Любая упорядоченная система двух неколлинеарных векторов a, b V2 образуют базис векторного пространства V2.
Доказательство.
Пусть a
и b
неколлинеарные вектора плоскости. По
следствию 2 теоремы 2 векторы a
и b
образует линейно независимую систему.
Пусть с
V2.
Отложим векторы a,
b
и с
от точки O:
a =
![]() ,
b
=
,
b
=
![]() и
с
=
и
с
=
![]() (см.
рис. 17). Проведем через точку C
прямую l,
параллельную прямой OB.
Так как векторы a
и b
неколлинеарны, то прямые OA
и
l
пересекаются в точке D.
Тогда
=
(см.
рис. 17). Проведем через точку C
прямую l,
параллельную прямой OB.
Так как векторы a
и b
неколлинеарны, то прямые OA
и
l
пересекаются в точке D.
Тогда
=![]() +
+![]() .
Так как векторы
и
соответственно
коллинеарны векторам a
и b,
то по свойству линейной зависимости
они
соответственно линейно выражается
через векторы a
и b:
=
a,
=
b. Поэтому
с =
=
a +
b, и по
определению 1 вектора a
и b
образует базис пространства
V2.
.
Так как векторы
и
соответственно
коллинеарны векторам a
и b,
то по свойству линейной зависимости
они
соответственно линейно выражается
через векторы a
и b:
=
a,
=
b. Поэтому
с =
=
a +
b, и по
определению 1 вектора a
и b
образует базис пространства
V2.
По теореме 3 базис векторов на плоскости образуют любые два неколлинеарные вектора, поэтому любой вектор на плоскости имеет две координаты. Тогда справедливо следующее утверждение.
Следствие 1. Вектора a = (1, 1), b = (2, 2) образуют базис векторов плоскости тогда и только тогда, когда
![]() =
0.
=
0.
Теорема 4. Векторы a, b и с компланарны тогда только тогда, когда они линейно зависимы.
Д оказательство.
Пусть вектора a,
b
и с
компланарны.
По определению они могут быть изображены
на одной плоскости .
Если вектора a,
b
коллинеарны, то по следствию 1 теоремы
2 они линейно зависимы. Тогда по свойству
по свойству линейной зависимости вектора
a,
b,
с
линейно зависимы. Если вектора a,
b
неколлинеарны, то по теореме 3 они
образуют базис векторов плоскости .
Тогда вектор с
линейная комбинация векторов a,
b,
и по свойству линейной зависимости
векторы a,
b,
с
линейно зависимы.
оказательство.
Пусть вектора a,
b
и с
компланарны.
По определению они могут быть изображены
на одной плоскости .
Если вектора a,
b
коллинеарны, то по следствию 1 теоремы
2 они линейно зависимы. Тогда по свойству
по свойству линейной зависимости вектора
a,
b,
с
линейно зависимы. Если вектора a,
b
неколлинеарны, то по теореме 3 они
образуют базис векторов плоскости .
Тогда вектор с
линейная комбинация векторов a,
b,
и по свойству линейной зависимости
векторы a,
b,
с
линейно зависимы.
Обратно, если векторы a, b, с линейно зависимы, то по свойству линейной зависимости, один из этих векторов линейно выражается через два другие. Тогда вектора могут быть изображены одной плоскости и поэтому коллинеарны.
Следствие 1. Векторы a, b и с некомпланарны тогда только тогда, когда они линейно независимы.
Базис векторов пространства. Рассмотрим множество V3 всех векторов пространства.
Теорема 5. Любая упорядоченная система трех некомпланарных векторов a, b, с V3 образуют базис векторного пространства V3.
Доказательство.
Пусть a,
b,
с некомпланарные
векторы. По следствию 1 теоремы 8 они
образует линейно независимую систему.
Пусть d
V3.
Отложим векторы a,
b,
с
и d
от точки O:
a =
,
b
=
,
с
=
,
d
=
(см. рис. 18). Проведем через точку D
прямую l,
параллельную прямой OD.
Так как векторы a,
b,
с
некомпланарны, т о
прямая l
пересекает плоскость OAB
в точке E.
Тогда
=
о
прямая l
пересекает плоскость OAB
в точке E.
Тогда
=![]() +
+![]() .
Так как векторы
лежит в плоскости OAB,
а вектора образуют базис векторов этой
плоскости, то по теореме 7
=
a +
b, где ,
R.
Так как вектор
коллинеарен вектору c,
то по
теореме 8 §
1 он
линейно выражается через вектор с:
=
с. Поэтому
d
=
=
a +
b +
с и по
определению 1 вектора a,
b,
с
образует базис пространства
V3.
.
Так как векторы
лежит в плоскости OAB,
а вектора образуют базис векторов этой
плоскости, то по теореме 7
=
a +
b, где ,
R.
Так как вектор
коллинеарен вектору c,
то по
теореме 8 §
1 он
линейно выражается через вектор с:
=
с. Поэтому
d
=
=
a +
b +
с и по
определению 1 вектора a,
b,
с
образует базис пространства
V3.
По теореме 5 базис векторов на пространстве образуют любые три некомпланарные вектора, поэтому любой вектор в пространстве имеет три координаты. Тогда справедливо следующее утверждение.
Следствие 1. Вектора a = (1, 1, 1), b = (2, 2, 2), с = (3, 3, 3) образуют базис векторов пространства тогда и только тогда, когда
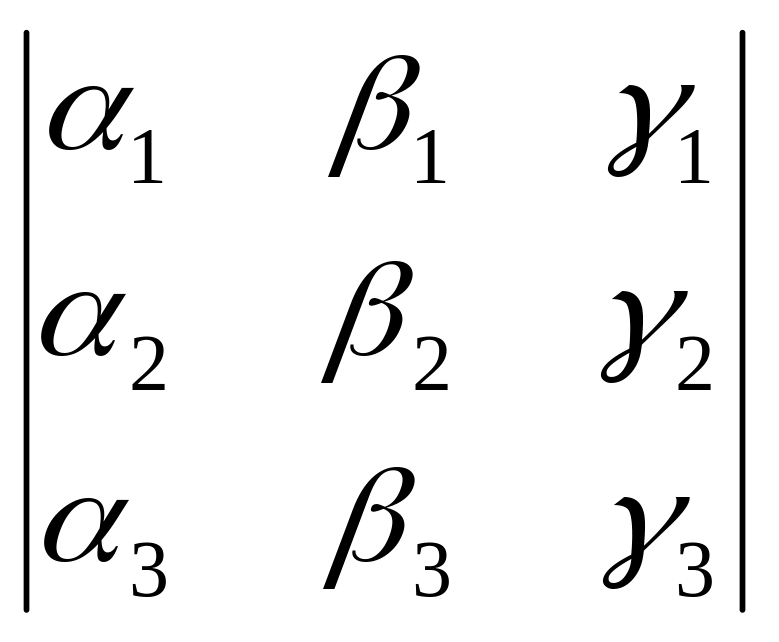 =
0.
=
0.
Теорема 6. Любые четыре вектора a, b, с, d в пространстве линейно зависимы.
Доказательство. Если векторы a, b, с компланарны, то по теоремы 5 они линейно зависимы. Тогда по свойству линейной зависимости по свойству 4 § 3 вектора a, b, с, d линейно зависимы. Если вектора a, b, с некомпланарны, то по теореме 5 они образуют базис векторов пространства. Тогда вектор d линейная комбинация векторов a, b, с и по свойству линейной зависимости векторы a, b, с, d линейно зависимы.
Задача 1. Доказать что векторы a = (1, 2, 0), b = (3, 2, 1), с = (0, 1, -1) образуют базис в пространстве и выразить вектор d = (5, 5, 2) через векторы базиса.
Решение. Так как определитель
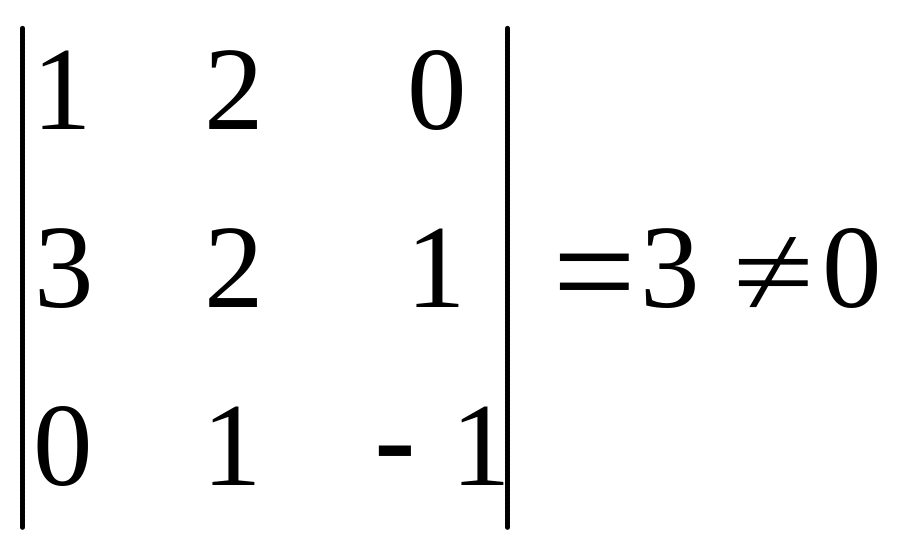 ,
,
то векторы a, b, с образуют базис пространства V3.
Для того, чтобы найти координаты вектора d в базисе a, b, с составим векторное уравнение
x a + y b + z c = 0. (14)
и запишем его в координатной форме:
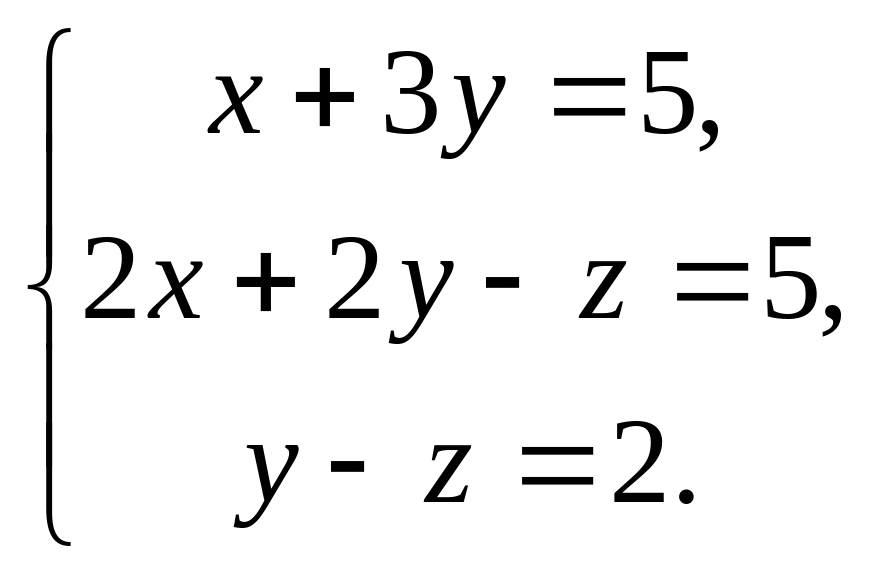
Решаем эту систему линейных уравнений: x = 2, y = 2, z = -1 и находим d = 2a + b - с.
