
Лекція з теоретичної фізики
Розділ: Вибрані задачі класичної механіки
Спеціальність 6.010100 Педагогіка і методика середньої освіти. Фізика.
Тема: Задача двох тіл та рух частинки у центрально-симетричному полі
План:
Задача двох тіл.
Рух частинки у центральному полі.
Закони Кеплера.
Космічні швидкості.
Література:
Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика: Учеб. Пособие. –В 10-ти т. Т.1. Механика. – М.: Наука, 1988, §§11–15.
И.В. Савельев. Основы теоретической физики, т. 1. – М.: Наука, 1975, §§11–12.
А.М. Федорченко. Класична механіка і електродинаміка. – К.: Вища школа, 1992, §§11–12.
В.В. Мултановский. Курс теоретической физики: Классическая механика. Основы специальной теории относительности. Релятивистская механика: учебное пособие для студентов физ.-мат. фак. пед. ин-тов. – М.: Просвещение, 1988, §27
Н.И. Жирнов Классическая механика: Учеб. Пособие для студентов физ.-мат. фак. пед. ин-тов. – М.: Просвещение, 1980, §§13,14,17–19
Задача двох тіл
Задача про рух двох частинок, що взаємодіють між собою, зводиться до задачі одного тіла і розв’язується повністю.
Вона може бути зведена до двох задач (одночастинних): задачі про рух центру мас; рух точки зведеної маси відносно центру мас.
Нехай, ми маємо систему з двох частинок
масами
![]() і
і
![]() .
.

Між ними діють сили взаємодії, а зовнішні сили відсутні. Тоді, рівняння, що описують рух цих частинок окремо матимуть вигляд:
![]()
![]() (1)
(1)
Оберемо нову систему відліку – систему із початком у центрі мас цих двох частинок.
![]() (2)
(2)
Ця система рухається із постійною
швидкістю. Коли центр (початок координат)
нової системи співпадає із точкою
![]() ,
то
,
то
![]() ,
тоді
,
тоді
![]() і
і
![]() – радіус-вектори
і
відносно
,
тоді маємо, що
– радіус-вектори
і
відносно
,
тоді маємо, що
![]() .
(3)
.
(3)
Значить, якщо знайти
,
тоді
![]() –
обчислити легко.
–
обчислити легко.
Введемо ще одну величину – відносну
координату:
![]() ,
,
тоді, помножуючи праву і ліву частину цього рівняння на отримаємо:
![]() (4)
(4)
Враховуючи рівняння (3) матимемо:
![]()
і підставимо в (4):
![]() ,
,
тоді матимемо, що:
![]() ;
;
![]() .
.
Тоді для швидкостей:
![]() ;
; ![]() (5)
(5)
А рівняння руху (1) набудуть вигляду:
![]()
![]()
![]()
Позначимо за
![]() й назвемо цю величину зведеною масою
й назвемо цю величину зведеною масою
Тоді ![]() .
.
Аналогічно:
![]() ,
або
,
або ![]() ,
тобто
,
тобто
![]() .
.
Отже, рух двох точок розглядається як рух однієї із зведеною масою
Із координатою під дією силового центру в початку координат.
К оли
вигляд силового поля
оли
вигляд силового поля
![]() відомий, то можна відшукати й
відомий, то можна відшукати й
![]() ,
а потім:
,
а потім:
![]() ,
,
![]() .
а також
.
а також
![]() ,
,
![]()
Таким чином, траєкторії руху заданих
точок
і
,
а також точки
![]() є подібні криві, відносно центру мас
системи, причому
є подібні криві, відносно центру мас
системи, причому
![]() .
Відповідно можна відшукати й швидкості
точок з рівнянь (5).
.
Відповідно можна відшукати й швидкості
точок з рівнянь (5).
Отже таким чином задача розв’язана.
Рух частинки у центральному полі
Як відомо, центрально-симетричне поле – це поле, в якому потенціальна енергія є функцією лише від віддалі від нерухомого центра до рухомої матеріальної точки, т. т.
![]()
Коли ми маємо дві матеріальні точки, то як ми вже бачили у попередньому питанні, їх рух може бути описаний в Ц-системі (системі пов’язаної із центром мас системи) як рух точки зведеної маси, т.т. зводиться до руху однієї точки..
Як відомо, момент імпульсу матеріальної
точки
![]() у центрально-симетричному полі є
інтегралом руху, тобто зберігається за
модулем і за напрямком, а якщо так
у центрально-симетричному полі є
інтегралом руху, тобто зберігається за
модулем і за напрямком, а якщо так
![]() і
і
![]() – лежать в одній площині перпендикулярній
до
– лежать в одній площині перпендикулярній
до
![]() ,
що не змінює свого положення в просторі
або іншими словами: рух – плоский.
Траєкторія такого руху – плоска крива,
а ому така тачка має лише дві ступені
вільності.
,
що не змінює свого положення в просторі
або іншими словами: рух – плоский.
Траєкторія такого руху – плоска крива,
а ому така тачка має лише дві ступені
вільності.
Т ому
для опису руху точки у центрально-симетричному
полі зручно використати полярну систему
координат: полюс (сумістити із центром
мас системи –
ому
для опису руху точки у центрально-симетричному
полі зручно використати полярну систему
координат: полюс (сумістити із центром
мас системи –
![]() ),
радіус вектор (його довжина (
),
радіус вектор (його довжина (![]() ),
азимут –
),
азимут –![]() .
Тобто площина
.
Тобто площина
![]() співпадає з полярною системою координат
співпадає з полярною системою координат
![]() ;
;
![]() .
.
![]()
![]()
Тоді у цій системі відліку момент імпульсу матеріальної точки має вигляд:
![]()
![]()
![]()
Отже, ![]() (1)
(1)
Повна енергія такої матеріальної точки:
![]() ,
або
,
або
![]() ;
;
![]() (2)
(2)
А тепер намітимо шлях розв’язання основної задачі механіки. Використовуючи отримані нами інтеграли руху (1) і (2) можна відшукати рівняння траєкторії матеріальної точки, а саме:
![]() і
і
![]()
Оскільки
![]() ,
тому
,
тому
![]() ;
;
![]()
![]() ,
значить
,
значить
![]() , (3)
, (3)
де
![]() – відцентрова потенціальна енергія.
– відцентрова потенціальна енергія.
Таким чином, можна ввести поняття ефективної потенціальної енергії:
![]() (4)
(4)
Ефективний потенціал (4) складається з
двох доданків, кожний з яких є функціями
лише координати
![]() і ефективний потенціал є функцією від
,
а тому отримане рівняння :
і ефективний потенціал є функцією від
,
а тому отримане рівняння :
![]() допускає розділення змінних:
допускає розділення змінних:
![]() ;
;
![]()
![]() ;
;

 (5)
(5)
Обчислити інтеграл (а це можна зробити
врахувавши відповідні граничні умови)
можна відшукати і
![]() .
.
Після цього:
;
![]() ;
;
![]() ;
;
Можна одержати рівняння руху і в загальному вигляді:
 ;
;
![]() ;
;

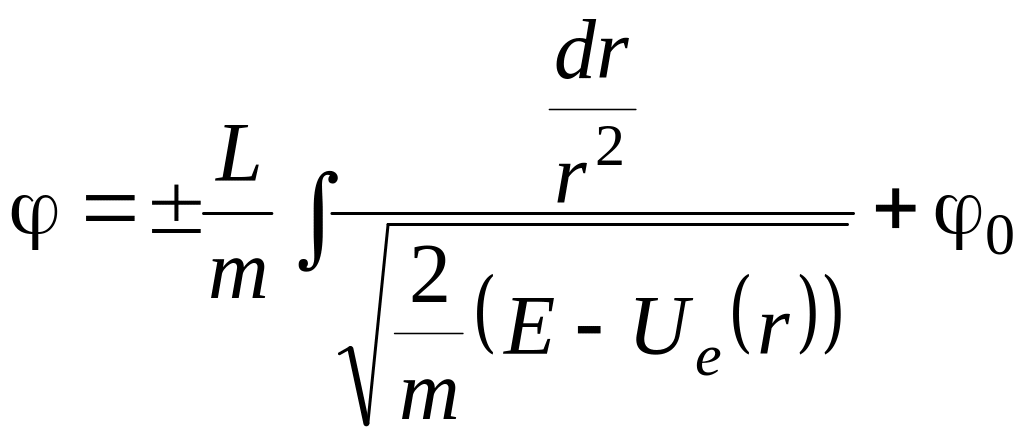 (6)
(6)
Це і є рівняння траєкторії
![]() .
.
Відзначимо особливості одержаних результатів.
З формули (6) випливає, що
 не змінюється, а тому
не змінюється, а тому
 – змінюється монотонно.
– змінюється монотонно.
може перетворюватись в нуль в точках де відповідно до рівняння (3):
![]()
![]() ;
;
![]()
Ці точки називають точками повороту, в
них змінюється
![]() ,
а
переходить від зростання до спадання
і навпаки.
,
а
переходить від зростання до спадання
і навпаки.
Область допустимих значень визначається з умови:
![]()
Коли ця умова виконується тоді
![]() ,
причому
,
причому
![]() і
і
![]() відмінні від
відмінні від
![]() і
і
![]() й рух частинки вважається фінітний,
коли
й рух частинки вважається фінітний,
коли
![]() ,
то рух – інфінітний.
,
то рух – інфінітний.
