Раздел III. Графовые модели.

1.Элементы теории графов.

Н

G: d→[i,j]

еориентированным графом называется тройка (I,D,G), в которой I – множество вершин, D – множество ребер и G – отображение, которое каждому ребру ставит в соответствие неупорядоченную пару вершин

Если каждому ребру соответствует упорядоченная пара вершин , то граф называется ориентированным графом, 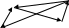а ребро называется дугой и обозначается (i,j).

ПРИМЕР 3.1.

а) неориентированный граф б) ориентированный граф

Путь – это упорядоченная последовательность дуг, начало каждой из которых совпадает с концом предыдущей. Контур – путь, у которого начальная вершина совпадает с конечной. Для неориентированного графа аналогом понятия путь является – цепь, а контура - цикл.

Простой цикл – цикл, в котором любая пара вершин соединена не более чем одним ребром. Гамильтонов цикл – простой цикл, проходящий через все вершины графа.

ПРИМЕР 3.2.

а) неориентированный граф б) варианты Гамильтонова цикла

Связный граф – граф, у которого любая пара вершин может быть соединена цепью (для неориентированного графа) или путем (для ориентированного графа)

Дерево – неориентированный граф без циклов.

Остов графа – подграф неориентированного графа, являющийся деревом.

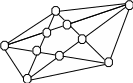
ПРИМЕР 3.3. Для предложенного графа существует 31 вариант остовов.

а) граф б) варианты остова

Если каждой вершине сопоставить число, то оно будет называться интенсивностью вершины. Если на множестве дуг задать числовую функцию, то каждое ребро приобретет вес.

П РИМЕР 3.4. Автомобилисту необходимо проехать из п.А в п.В.

10 0

А 7 В

4 2

Ориентированный связный граф, вершинам которого сопоставлены числа (интенсивности, пропускные способности) или дугам которого сопоставлены числа (стоимости, протяженности, пропускные способности), принято называть сетью.

Потоком на сети называется совокупность величин, заданных на множестве дуг, {x_d}:

,

где – множество дуг, исходящих из вершины i, а – множество дуг, входящих в нее; b_i – интенсивность вершины i.

Величина x_d называется значением потока по дуге d и интерпретируется как количество продукта, пропускаемое по данной дуге

Сеть с заданными пропускными способностями дуг будем считать реальной, если в ней каждой выходящей дуге сопоставлено число, не превышающее суммарную пропускную способность всех входящих в соответствующую вершину дуг.

ЗАДАЧИ ОПТИМИЗАЦИИ НА СЕТИ.

1. Об оптимальном распределении грузопотоков на сети (транспортная задача)

2. О кратчайшем пути между двумя пунктами (вершинами.)

3. О совокупности дорог, соединяющих пункт отправления со всеми пунктами назначения (минимальный остов)

4. Об оптимальном пути для коммивояжера (оптимальный Гамильтонов цикл)

5. О максимальном потоке на сети.

2. Задача о кратчайшем пути.

ЗАДАЧА. Задан неориентированный граф. Функция стоимости - c_ij. Найти оптимальный путь между двумя вершинами.

АЛГОРИТМ МИНТИ.

1. Введем переменную c^/_ij =c_ij в начальный момент.

2. Пометим начальную вершину числом m₀=0.

3. Для каждой помеченной вершины i будем метить те вершины, которые можно достичь из I по дугам с нулевым значением, т.е. m_j=i еще не помеченные вершины j для которых c^/_ij=0. Пометки расставляем до тех пор, 1) пока не пометим конечную вершину пути или 2) пока нельзя будет сделать дальнейшие пометки. В случае 1) искомый путь (определяется по пометкам) найден и задача решена.

4. Для всех помеченных вершин I определим

5. Уменьшим c^/_ij при 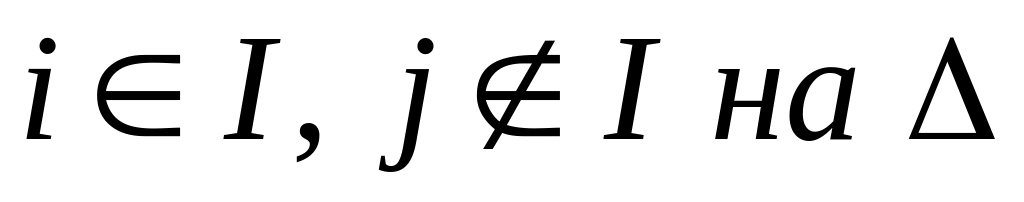и перейдем к п.3

ПРИМЕР 3.5.

М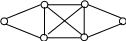 9 К

2 2 4 3

А 3 1 2 7 В

Р 5 Т

Пометим вершину А числом m_A=0. Так как дальнейшая пометка невозможна, переходим к п.4: Δ=2, c^/_АМ=0, c^/_АР=1

Пометим вершину М: m_М=А. Δ=1, c^/_МР=0, c^/_АР=0, c^/_МТ=1, c^/_МК=8

Пометим вершину Р: m_Р=А. Δ=2, c^/_РК=3, c^/_РТ=4, c^/_МТ=0, c^/_МК=7

Пометим вершину Т: m_Т=М. Δ=2, c^/_ТВ=5, c^/_ТК=0

Пометим вершину К: m_К=Т. Δ=3, c^/_КВ=0

Пометим вершину В: m_В=К

Получили оптимальный путь: A→M→T→K→В. Длина пути=11

МЕТОД расстановки пометок.

ДАНО: (I,D,G) – неориентированный граф;

L(i,j) – длина ребра [i,j];

n, k – начальная и конечная вершины цепи.

НАЙТИ: min L(n, k)

АЛГОРИТМ

1. Пометим каждую вершину индексом λ_i

2. Примем λ_k =0; все остальные λ_i =∞

3. Найдем ребро (i,j), для которого λ_j –λ_i >L(i,j) и заменим λ_j =λ _j +L(i,j)

4. Продолжим процесс до тех пор, пока существует хотя бы одно ребро, для которого можно уменьшить λ_j

5. Найдем путь движением от начальной вершины к конечной по убыванию индексов переходом по дугам, для которых λ_i –λ_j =L(i,j)

П

4 В

2 3

А

РИМЕР 3.6. Найти кратчайший путь от А до В.

3 4 2

1

5 2 2

5 2

2

3 3 4 3

2 4 1

3

РЕШЕНИЕ