5. Простейшие системы массового обслуживания.

n-канальная СМО с отказами. (задача Эрланга).

ПРИМЕРЫ. Телефонная станция.

Рассмотрим одну из первых по времени, «классических» задач теории массового обслуживания; эта задача возникла из практических нужд телефонии и была решена в начале нашего века датским математиком Эрлангом.

ДАНО.

n – количество каналов (линий связи),

λ – интенсивность потока заявок (1/t_з ).

 – интенсивность потока обслуживании (1/t_об ).

НАЙТИ.

p_i – финальные вероятности состояний СМО

характеристики ее эффективности:

A — абсолютную пропускную способность, т. е. среднее число заявок, обслуживаемых в единицу времени;

Q — относительную пропускную способность, т, е. cреднюю долю пришедших заявок, обслуживаемых системой;

P_отк —вероятность отказа, т. е. того, что заявка покинет СМО необслуженной;

k — среднее число занятых каналов.

РЕШЕНИЕ. Cостояния системы S будем нумеровать по числу заявок, находящихся в системе (в данном случае оно совпадает с числом занятых каналов):

S_о — в СМО нет ни одной заявки,

S₁ — в СМО находится одна заявка (один канал занят, остальные свободны),

S_k —в СМО находится k заявок (k каналов заняты, остальные свободны),

S_n — в СМО находится п заявок (все п каналов заняты).

Граф состояний СМО соответствует схеме гибели и размножения.

λ λ λ λ λ λ λ

 2 3 k (k+1) (n-1) n

Разметим этот граф, т.е. проставим у стрелок интенсивности потоков событий. Из S₀ в S₁ систему переводит поток заявок с интенсивностью λ (как только приходит заявка, система перескакивает из S₀ в S₁ ). Тот же поток заявок переводит систему из любого левого состояния в соседнее правое. Проставим интенсивности у нижних стрелок. Пусть система находится в состоянии S₁ (работает один канал). Он производит  обслуживаний в единицу времени. Проставляем у стрелки S₁ - S₀ интенсивность . Теперь представим себе, что система находится в состоянии S₂ (работают два канала). Чтобы ей перейти в S₁ нужно, чтобы либо закончил обслуживание первый канал, либо второй; суммарная интенсивность их потоков обслуживании равна 2; проставляем ее у соответствующей стрелки. Суммарный поток обслуживаний, даваемый тремя каналами, имеет интенсивность 3, n каналами — n. Проставляем эти интенсивности у нижних стрелок.

А теперь, зная все интенсивности, воспользуемся уже готовыми формулами для финальных вероятностей в схеме гибели и размножения.

Обозначим , тогда и

Вероятность того, что заявка не будет обслужена, равна вероятности того, что все каналы заняты, следовательно

Относительную пропускную способность – это вероятность того, что заявка будет обслужена Q=1-P_отк

Абсолютная пропускная способность А= Q

А можно расценивать как интенсивность потока обслуженных заявок. Каждый занятый канал в единицу времени обслуживает  заявок. Тогда среднее количество занятых каналов k=A/

Одноканальная СМО с неограниченной очередью.

ПРИМЕРЫ.

Врач, обслуживающий пациентов; будка с телефоном-автоматом.

ЗАДАЧА. Построить модель одноканальной СМО с очередью.

ПРЕДПОЛОЖЕНИЯ. Очередь не ограничена по времени ожидания и по длине.

ДАНО.

n=1 – число каналов

λ – интенсивность потока заявок

μ – интенсивность потока обслуживания.

НАЙТИ.

Р_i– финальные вероятности системы.

L_сист – среднее число заявок в системе

W_сист – среднее время пребывания заявки в системе

L_оч – среднее число заявок в очереди

W_оч – среднее время пребывания заявки в очереди.

P_зан – вероятность того, что канал занят.

РЕШЕНИЕ.

S₀ – канал свободен;

S₁ – канал занят, очереди нет (в системе одна заявка);

S₂ – канал занят, одна заявка в очереди;

…

S_k – канал занят, k-1 заявка стоит в очереди;

…

Построим граф состояний:

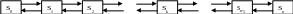λ λ λ λ λ λ λ λ

μ μ μ μ μ μ μ μ

P₀=(1+λ/μ+ (λ/μ)²+(λ/μ)³+…(λ/μ)^k+…)^-1=(1+ ρ + ρ ²+…+ ρ ^k+…)^-1=1/(1- ρ) при ρ <1

При ρ ≥1 ряд расходится, т.е. предельные вероятности не существуют. Это говорит о том, что очередь неограниченно растёт, т.е. система перегружена.

При ρ =1 СМО справляется только с регулярным потоком заявок с временем обслуживания равным интервалу между заявками.

P₀=1- ρ

P₁= ρ (1- ρ)

P₂= ρ ²(1- ρ)

…

Среднее число заявок в системе = математическому ожиданию числа заявок:

L_сист=(0*Р₀+1*Р₁+2*Р₂+…+k*P_k+…

По формуле Литтла:

Среднее число заявок в очереди = среднему числу заявок в системе – среднее число заявок под обслуживанием. Число заявок под обслуживанием в одноканальной системе может быть либо 0, либо 1. Вероятность того, что канал свободен =Р₀. Вероятность того, что канал занят P_зан =1-Р₀=ρ. Эта вероятность и есть среднее число заявок, находящихся под обслуживанием.

L_оч= L_сист–ρ=

n-канальная СМО с неограниченной очередью.

ПРИМЕРЫ.

Кассы, обслуживающие покупателей; переговорная станция.

ЗАДАЧА. Построить модель n-канальной СМО с очередью.

ПРЕДПОЛОЖЕНИЯ. Очередь не ограничена по времени ожидания и по длине.

ДАНО.

n – число каналов

λ – интенсивность потока заявок

μ – интенсивность потока обслуживания.

НАЙТИ.

Р_i– финальные вероятности системы.

L_сист – среднее число заявок в системе

W_сист – среднее время пребывания заявки в системе

L_оч – среднее число заявок в очереди

W_оч – среднее время пребывания заявки в очереди.

P_зан – вероятность того, что канал занят.

РЕШЕНИЕ.

S₀ – каналы свободны;

S₁ – 1 канал занят, остальные свободны (в системе одна заявка);

S₂ – 2 канала занято, остальные свободны;

…

S_k – k каналов занято, остальные свободны;

…

S_n – все каналы заняты, очереди нет;

S_n+1 – все каналы заняты, одна заявка в очереди;

S_n+2 – все каналы заняты, две заявки в очереди;

…

S_n+r – все каналы заняты, r заявок стоит в очереди;

…

Построим граф состояний:

λ λ λ λ λ λ λ λ

μ 2μ 3μ nμ nμ nμ nμ nμ

Обозначим ρ = λ/μ

p₀=(1+ ρ + ρ ²/2+ ρ ³/3!…+ ρ ⁿ/n!+ ρ ⁿ⁺¹/(n!(n- ρ)) )^-1 при ρ /n<1

При ρ/n ≥1 ряд расходится, т.е. предельные вероятности не существуют. Это говорит о том, что очередь неограниченно растёт, т.е. система перегружена.

P₁= ρ P₀

P₂=P₀ ρ ²/2!

…

P_n=P₀ ρ ⁿ/n!

,

k= λ/μ – среднее число занятых каналов для любой СМО с неограниченной очередью.

Среднее число заявок в очереди = математическому ожиданию числа заявок в очереди:

L_оч=(1* P_n+1+2* P _n+2+…+r* P_n+r+…

Среднее число заявок под обслуживанием L_обс = k = ρ

Среднее число заявок в системе L_cис= L_оч +L_обс

Одноканальная СМО с ограниченной очередью.

ПРИМЕРЫ.

Врач, обслуживающий пациентов по талонам.

ЗАДАЧА. Построить модель одноканальной СМО с ограниченной очередью.

ДАНО.

n=1 – число каналов

k – max длина очереди

λ – интенсивность потока заявок

μ – интенсивность потока обслуживания.

НАЙТИ.

Р_i– финальные вероятности системы.

L_сист – среднее число заявок в системе

W_сист – среднее время пребывания заявки в системе

L_оч – среднее число заявок в очереди

W_оч – среднее время пребывания заявки в очереди.

P_зан – вероятность того, что канал занят.

РЕШЕНИЕ.

S₀ – канал свободен;

S₁ – канал занят, очереди нет (в системе одна заявка);

S₂ – канал занят, одна заявка в очереди;

…

S_k+1 – канал занят, k заявок стоят в очереди;

Построим граф состояний:

λ λ λ λ

μ μ μ μ

P₀=(1+λ/μ+ (λ/μ)²+(λ/μ)³+…(λ/μ)^k+1)^-1=(1+ ρ + ρ ²+…+ ρ ^k+1)^-1

Замкнутая СМО с одним каналом и m источниками заявок.

ПРИМЕРЫ.

Оператор, обслуживающий группу станков.

ЗАДАЧА. Построить модель одноканальной СМО с ограниченным источником заявок.

ДАНО.

n=1 – число каналов

m – max число заявок

λ – интенсивность потока заявок

μ – интенсивность потока обслуживания.

НАЙТИ.

Р_i– финальные вероятности системы.

L_сист – среднее число заявок в системе

W_сист – среднее время пребывания заявки в системе

L_оч – среднее число заявок в очереди

W_оч – среднее время пребывания заявки в очереди.

P_зан – вероятность того, что канал занят.

РЕШЕНИЕ.

S₀ – канал свободен;

S₁ – канал занят, очереди нет (в системе одна заявка);

S₂ – канал занят, одна заявка в очереди;

…

S_m – канал занят, m-1 заявка в очереди;

Построим граф состояний:

mλ (m-1)λ (m-2)λ λ

μ μ μ μ

P₀=(1+mλ/μ+ m(m-1)(λ/μ)²+m(m-1)(m-2)(λ/μ)³+…m!(λ/μ)^m)^-1=

=(1+ mρ + m(m-1)ρ²+…+ m!ρ ^m)^-1