3. Кратчайший путь в ориентированном графе.

Обозначим Г(х) – множество конечных вершин дуг исходящих из x, а Г^-1(х) – множество начальных вершин дуг, входящих в х.

Порядковой функцией О(х) назовем функцию, определенную на множестве вершин: если x_j Є Г(x_i), то O(x_j)>O(x_i), т.е. если вершина x_j следует за вершиной x_i, то значение порядковой функции в ней больше, чем в x_i Величину O(x_i) будем называть уровнем вершины x_i.

ЗАДАЧА. Задан ориентированный граф G=(X,U) без циклов и числовая функция на дугах. Построить минимальный путь из вершины А в вершину В.

ТЕОРЕМА ОПТИМАЛЬНОСТИ. Если некоторый путь, соединяющий вершины x_i и x_j , является минимальным, то его подпуть также является минимальным.

АЛГОРИТМ БЕЛЛМАНА.

1. Построим порядковую функцию О(х), полагая О(А)=0.

2. Начиная с вершины В, рассматриваем последовательно все вершины графа в порядке убывания его порядковой функции и приписываем каждой вершине число, равное минимальному значению пути от этой вершины до В.

ПРИМЕР 3.7.

М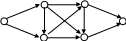 9 К

2. 2 4 3

А 1 2 В

3 7

Р 5 Т

1. О(А)=0, О(М)=1, О(Р)=2, О(К)=3, О(Т)=4, О(В)=5

2. S(T)=7, S(K)=min(9,3)=3, S(P)=min(7,12)=7, S(M)=min(12,9,8)=8, S(A)=min(10,10)=10

Минимальный путь А→Р→К→В

АЛГОРИТМ ФОРДА.

1. Положим λ_i=∞ в каждой вершине, кроме λ₀=0

2. Ищем дугу (x_i , x_j ) : λ_j -λ_i >l(x_i , x_j ) и заменяем λ_j на λ_i+l(x_i , x_j ) <λ_j Поступаем так до тех пор, пока возможно найти дугу, уменьшающую хотя бы одно значение.

ПРИМЕР 3.8.

М 9 К

2 2 4 3

А 1 2

3 1 7 В

Р 5 Т

λ_А =0, λ_Р =3 λ_М =2,λ_К=7, λ_Т=8, λ_В=10

ПРИЛОЖЕНИЕ ЗАДАЧИ.

1. Планирование транспортных маршрутов

2. Прокладка магистрали между двумя объектами

3. Установление последовательности взаимосвязанных работ

4. Построение графа наименьшей длины.

ЗАДАЧА. Дан неориентированный граф. Построить связный подграф, имеющий минимальную суммарную длину входящих в него ребер.

ДАНО. (I,D,G) – неориентированный граф;

L(i,j) – длина ребра [i,j];

НАЙТИ. (I,D,G) – неориентированный связный граф, для которого достигается

АЛГОРИТМ.

1. Строим самое короткое ребро. Если имеется несколько ребер одинаковой длины, выбираем любое из них.

2. Из оставшихся ребер выбираем самое короткое, которое в совокупности е уже имеющимися не образует циклов.

3. процесс продолжается до тех пор, пока не будут исчерпаны все ребра.

ПРИМЕР 3.9. Построить граф наименьшей длины.

4

2 3

3 4 2

1

5 2 2

5 2

2

3 3 4 3

2 4 1

3

РЕШЕНИЕ:

Получившийся граф

5. Транспортная задача в сетевой постановке.

ПОСТАНОВКА ЗАДАЧИ.

Имеется сеть (I,D,G) с заданными стоимостями перемещения единицы продукта по дуге c_d и интенсивностями вершин b_i::

b_i >0 – для пунктов отправления, i – источник;

b_i <0 – для пунктов назначения, i – сток;

b_i =0 – для нейтральных вершин.

Требуется найти оптимальный поток, для которого

При ограничениях ,

КРИТЕРИЙ ОПТИМАЛЬНОСТИ. Для того, чтобы допустимый поток был оптимальным, необходимо и достаточно существование для каждой вершины i такого числа v_i, называемого потенциалом, что для всех дуг d=(i,j)

v_j - v_i ≤ c_d , если x_d =0

v_j - v_i =c_d , если x_d >0

АЛГОРИТМ МЕТОДА ПОТЕНЦИАЛОВ.

1. Найдем допустимый невырожденный поток.

а) с помощью транспортной таблицы;

б) с помощью вспомогательной задачи:

к множеству вершин сети добавим фиктивную вершину с b₀ =0, все вершины, для которых b_i<0 соединим с нулевой вершиной входящими дугами (0,i), а для которых b_i>0 – исходящими (i,0), стоимость транспортировки для вновь добавленных дуг положим равными 1, а для остальных =0.

2. Проверим оптимальность текущего потока.

Строим систему потенциалов:

произвольно выбираем пункт i, потенциал которого полагаем равным 0;

вычисляем потенциалы вершин для которых x_d >0 по правилу

v_j = v_i +c_d , если дуга направлена от i

v_j = v_i -c_d , если дуга направлена к i

Проверяем условие оптимальности:

Если условие оптимальности выполнено, то текущий поток является оптимальным. Вычислительный процесс завершаем.

Если не выполнено, то переходим к следующему пункту.

3. Определим дугу, вводимую в поток.

Выберем ту дугу d_k, для которой достигается максимальное отклонение цены от разности потенциалов, соединяемых вершин.

4. Построим цикл.

Цикл должен содержать дугу d_k и дуги, для которых x_d >0

5. Преобразуем текущий поток.

Среди всех дуг цикла рассмотрим дуги, ориентация которых не совпадает с ориентацией дуги d_k и найдем Δ=min x_d

Преобразуем поток, добавляя Δ для всех сонаправленных с d_k дуг и отнимая Δ для всех противоположно направленных дуг.

Перейдем к пункту 2.