3. Геометрическая интерпретация озлп.

Пусть r=2 и свободными переменными являются x₁ , x₂ , тогда m уравнений можно записать в виде:

Построим на плоскости x₁Оx₂ прямые x₃ =0, x₄ =0, … x_n =0. Так как все элементы допустимого решения должны быть неотрицательными, то для каждого элемента решения допустимой является только одна полуплоскость, в которой x_i>0. Часть первого координатного угла, принадлежащая одновременно всем этим полуплоскостям и есть ОДР.

Целевую функцию также выразим через свободные переменные.

Максимум этой функции достигается при тех же значениях переменных, что и максимум однородной функции (без свободного члена).

Построим на плоскости прямую Назовем ее опорной прямой. Мысленно двигая эту прямую в сторону возрастания, заметим, что максимум достигается в одной из вершин ОДР, где по крайней мере 2 базисные переменные обращаются в нуль.

Если целевая функция в ОДР не ограничена сверху, то оптимального решения не существует. Если максимум достигается не в одной точке, а совпадает с границей ОДР, то существует бесконечное множество оптимальных решений.

ПРИМЕР 2.2. (условие в п.1)

Математическая модель:

х _i – количество ткани i-го вида (м)

х_i 0

L= х₁+х₂max

{

{

х3 =10 - х1 -2х2 х4 = -8+ х1 + х2 L= х1+х2max

х2 =5 –0.5 х1 х2 = 8- х1 опорная прямая: х2 = -х1

8 х₂

5 х₄ =0

х₃ =0

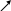
. 8 10

х₁

Ответ: х₂ =0; х₁ =10; L=10

Анализ.

1. Для получения максимальной прибыли фабрике следует выпускать только ткань 1-го вида количество 10м. Но тогда все лилипуты будут чем-то похоже друг на друга.

2. Можно повысить цену на ткань 2-го вида в 2раза. Тогда целевая функция будет иметь вид: L= х₁+2х₂ , а опорная прямая: х₂ = - 0.5х₁ В этом случае ОЗЛП будет иметь бесконечное множество оптимальных решений на отрезке.

3. Чтобы задача не имела оптимального решения, ОДР а) должна быть не ограничена сверху или б) не существовать вообще.

а) Область положительности х₃ должна быть направлена в ту же сторону, что и для х₄ Этого можно добиться, если не ограничивать сверху расход сырья.

б) Решений не будет существовать вообще, если прямые пересекутся ниже оси абсцисс. Например, ограничение на суточный расход станет ниже 8ед. или суточный спрос на ткань превысит 10м

ПРИМЕР 2.4. (условие в п.2)

Опорная прямая:

14

5

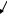
10 14

Ответ: х₁=0; х₂=5; L’=-15; L=15

ЗАМЕЧАНИЯ.

1. Если система ограничений задачи линейного программирования содержит всего 2 переменные, то область допустимых решений можно найти, решив систему неравенств.

2. Построить опорную прямую можно, опираясь на то, что она перпендикулярна вектору нормали.

ПРИМЕР 2.5. Магазин закупает печенье 2-х сортов по цене с_i за 1 кг i-ого вида и получает прибыль p_i от его реализации. Денежный ресурс ограничен А. Спрос покупатель не превышает В. Максимизировать прибыль при условии полного удовлетворения спроса.

	цена	прибыль	количество
1 сорт	20	3	х1
2 сорт	10	1	х2
Условия	≤ 600	max	≥ 50

ПРИМЕЧАНИЯ.

1. Для построения ОДР можно не добавлять дополнительные переменные. Достаточно просто решить систему неравенств.

2. Опорную прямую можно строить с помощью вектора нормали. Координатами вектора нормали являются коэффициенты при переменных в целевой функции. Вектор нормали показывает направление возрастания целевой функции. Опорная прямая проводится перпендикулярно вектору нормали. В примере N=(3,1)

60

50

30 50

Анализ.

1. Следует покупать печенье обоих сортов, т.к. покупка только 1 сорта (наиболее прибыльного) не удовлетворяет спрос населения.

Оптимальное решение достигается в точке пересечения двух прямых. Найдем эту точку, решив систему уравнений:

х₁=10; х₂=40; L=70

2. Бесконечного множества решений можно достигнуть, повысив цену реализации на 2 сорт или понизив цену на 1 сорт так, чтобы прибыль от продажи была пропорциональна закупочной цене.

3. Решения не будет существовать (ОДР – пустое множество), если спрос покупателя увеличится и станет более 60.

4. Если закупочная сумма неограниченна, то оптимального решения не будет

(ОДР не ограничена сверху)

Задание 2.1. Рассмотрим пример 2.5. со следующими данными.

	цена	прибыль	количество
1 сорт	20	3	х1
2 сорт	10	2	х2
Условия	≤ 1000	max	≥ 50

ОТВЕТ: х₁=5;0 х₂=0; L=15

ПРАВИЛО. Оптимальное решение ОЗЛП (если оно существует) достигается при такой совокупности значений переменных x₁ , x₂ , …, x_n,, где по крайней мере k=n-m из них обращаются в нуль, а остальные неотрицательны.

Отсюда вытекает идея метода «последовательных проб».

а) выбираем k свободных переменных и полагаем их равными 0;

б) вычисляем значения базисных переменных при нулевых значениях сводных.

Если все они оказались неотрицательными, значит мы нашли допустимое (необязательно оптимальное) решение.

Для простых задач, где число переменных невелико, «слепой перебор» может привести к оптимальному решению довольно быстро.

ПРИМЕР 2.4.

№	x1	x2	x3	x4	L
	0	0	-60	14	Решение не допустимое
	0	14	108	0	52
	14	0	24	0	28
	0	5	0	9	15
	10	0	0	4	20
	18	-4	0	0	Решение не допустимое

ПРИМЕР 2.5.

№	X1	x2	x3	x4	L
	0	0	600	-50	Решение не допустимое
	0	50	100	0	50
	50	0	-400	0	Решение не допустимое
	0	60	0	10	60
	30	0	0	-20	Решение не допустимое
	10	40	0	0	70

Но в практических задачах число переменных очень велико, порядка сотен. Для таких задач простой перебор становится невозможным. Например, при n=30, m=10 число переборов свободных переменных свыше 30 миллионов!