10.2. Линейная модель обмена (модель международной торговли)

Рассмотрим n стран (n N): S₁, S₂, ..., S_i, ..., S_n с известным национальным доходом x₁, x₂,..., x_i, ..., x_n соответственно.

Пусть a_ij - запланированная доля национального дохода страны S_j на покупку товаров у страны S_i, ( ). Числа a_ij можно записать в виде матрицы

.

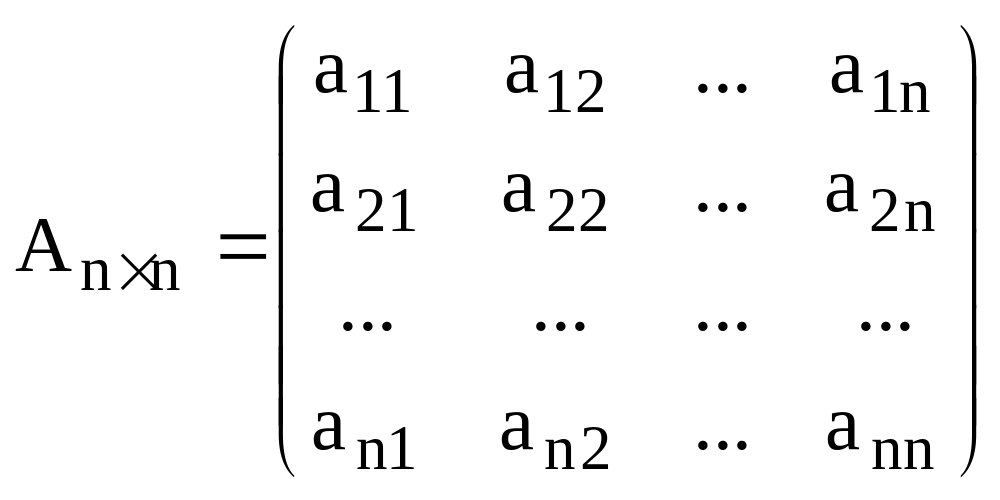В этой задаче квадратную матрицу А называют структурной матрицей торговли.

Будем считать, что весь национальный доход каждой страны S_i используется только на закупку товаров либо внутри самой страны ( ), либо на импорт из других стран ( ) . Естественно, что в матрице А элементы неотрицательны и в каждом столбце сумма всех элементов равна единице.

Из перечисленных выше условий следует, что сбалансированная торговля возможна только при условии .

При получим систему линейных уравнений, которую в матричной форме можно записать как (*) ,

где А -структурная матрица торговли, а - вектор национальных доходов по странам.

Из уравнения следует, что вектор Х можно рассматривать, как собственный вектор матрицы А с собственным числом . Следовательно, только собственный вектор структурной матрицы торговли с собственным числом даст национальные доходы стран, обеспечивающие сбалансированность торговли.

Пример. Дана структурная матрица торговли трех стран: .

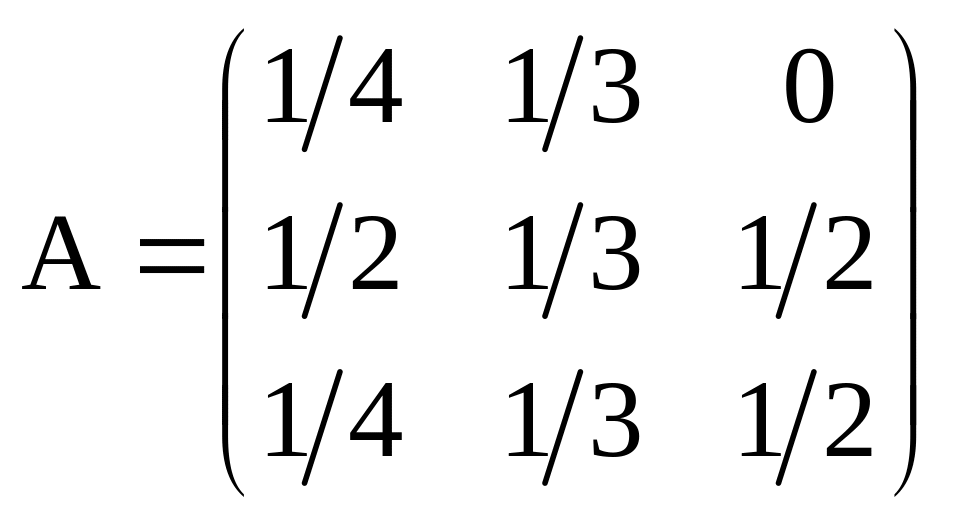Определить, при каких национальных доходах этих стран торговля между ними будет сбалансированной.

Найдем собственный вектор матрица А при . Для этого достаточно найти вектор Х из матричного уравнения . . .

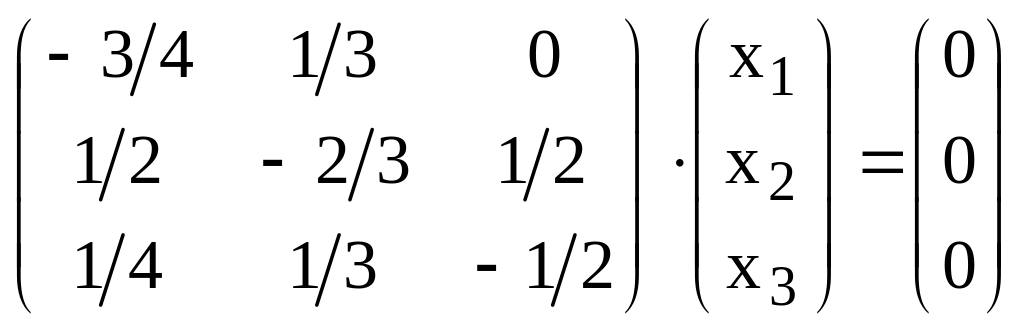После умножения всех уравнений на 12 расширенная матрица этой системы будет иметь вид: .

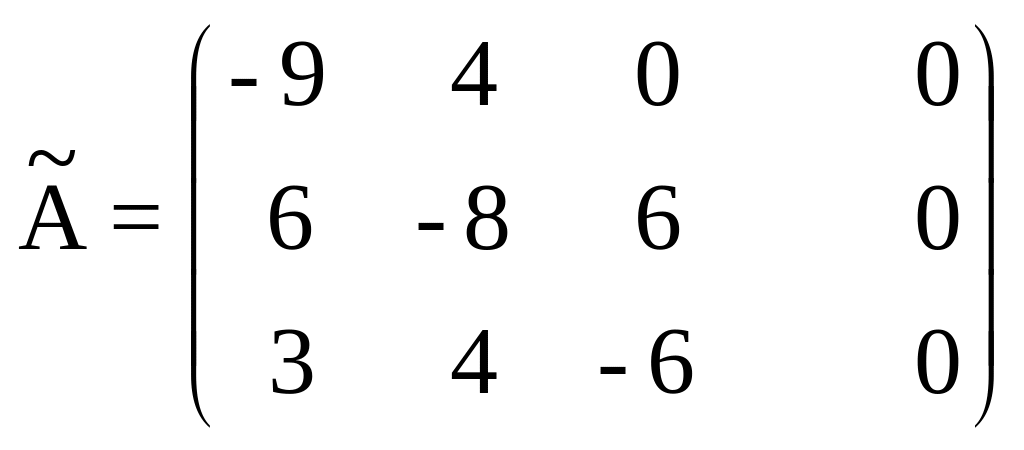Метод полного исключения приводит к результатам:

.

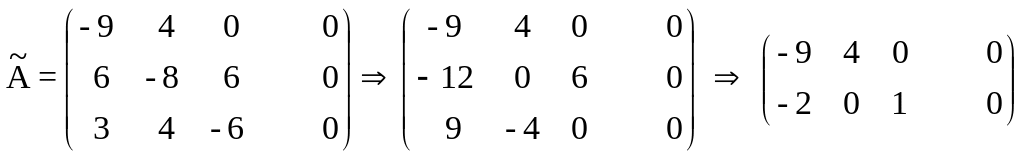Получили однородную систему двух линейных уравнений с тремя неизвестными. Однородная система всегда разрешима. Количество неизвестных равно 3, а ранг расширенной матрицы и матрицы системы равен 2, следовательно, система имеет бесчисленное множество решений, зависящих от оного параметра ( 3-2=1 ) . Пусть x₁ =4t, тогда x₂ =9t, x₃ = 8t, где t - параметр. Это означает, что при данной структурной матрице торговля будет сбалансированной только при условии, что отношение национальных доходов этих стран будет равно 4 : 9 : 8 .

11. Метод полного исключения для решения системы линейных уравнений

Примечание Этот раздел является повторением необходимого для использования в данном семестре

материала первого семестра.

Метод полного исключения можно использовать для решения любой системы линейных алгебраических уравнений. Рассмотрим алгоритм этого метода на примере.

Пусть дана система линейных уравнений (1).

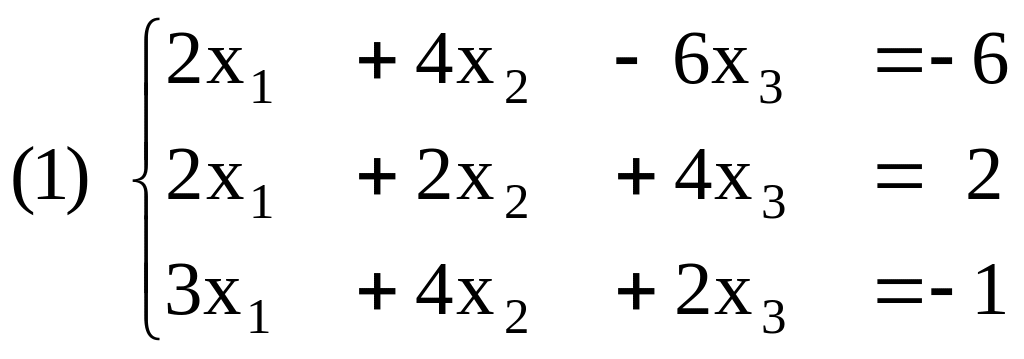
Расширенная матрица этой системы имеет вид (2).

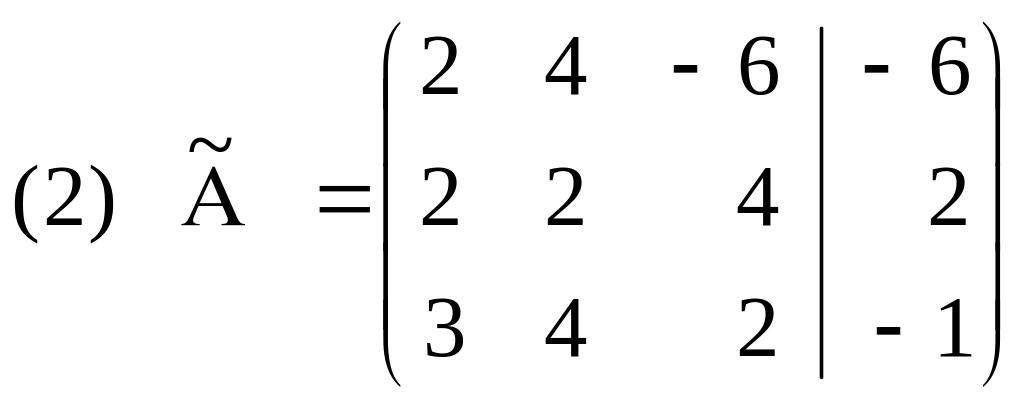
1. Первый шаг решения (I шаг) состоит в следующем.

1.1. Выбираем строку, у которой первый элемент не равен нулю (в нашем примере можно взять, например, первую строку). Эту строку назовем «разрешающая (ведущая) строка первого шага». Первый столбец назовем «разрешающий (ведущий) столбец первого шага», а элемент, расположенный на пересечении разрешающей строки и разрешающего столбца назовем «разрешающий (ведущий) элемент первого шага». Эта операция соответствует перемене местами уравнений системы, поэтому новая система будет равносильна исходной.

1.2. Разрешающую (первую) строку делим на разрешающий элемент. Получаем новую строку ( ), которую записываем первой строкой в новой матрице . При этом новая матрица примет вид:

.

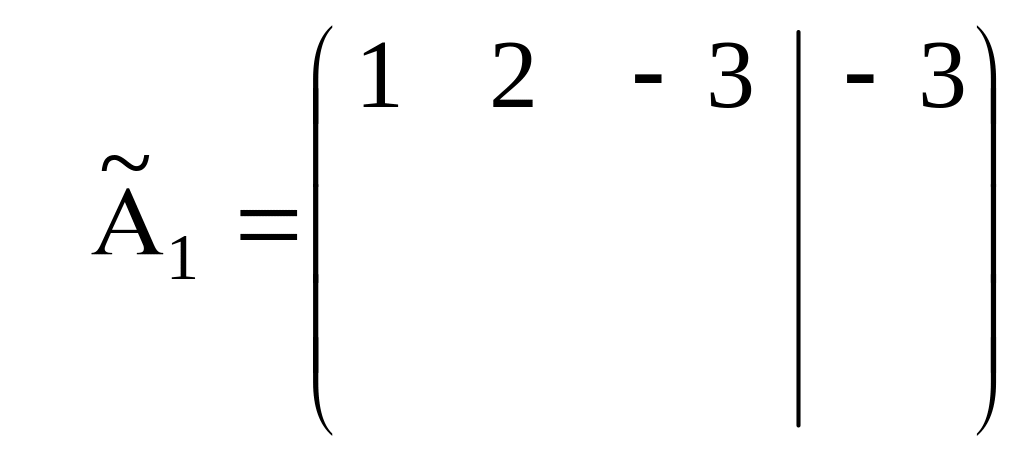1.3. Чтобы найти вторую строку матрицы ,ко второй строке матрицы прибавим новую первую строку из матрицы , предварительно умножив ее на такое число, чтобы в первом столбце оказался ноль. В нашем примере ко второй строке матрицы нужно прибавить первую строку матрицы , умноженную на (-2), получим:

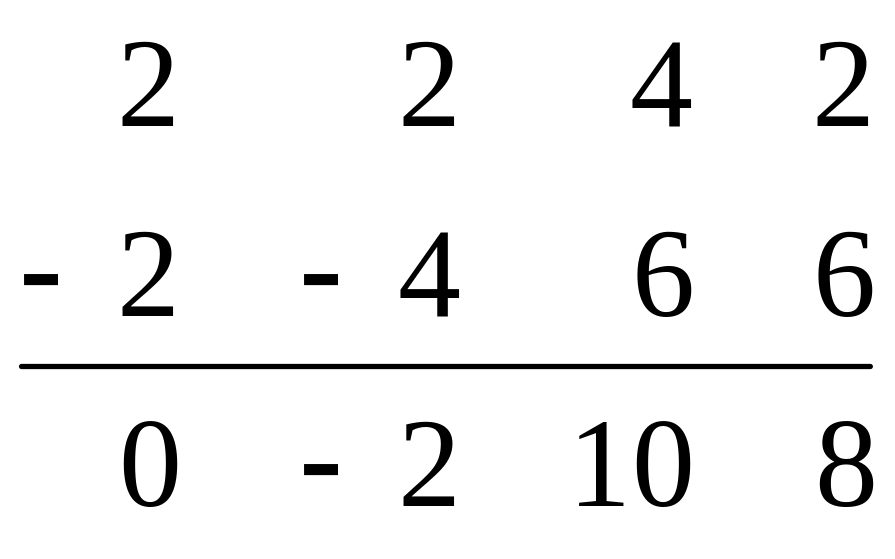
Теперь матрица будет иметь вид:

.

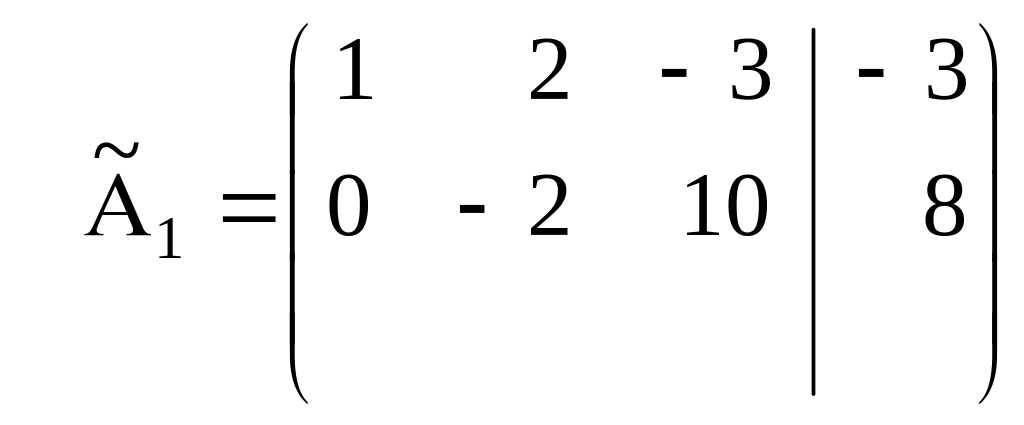1.4. Чтобы найти третью строку матрицы ,к третьей строке матрицы прибавим новую первую строку из матрицы , предварительно умножив ее на такое число, чтобы в первом столбце оказался ноль. В нашем примере ко второй строке матрицы нужно прибавить первую строку матрицы , умноженную на (-3), получим:

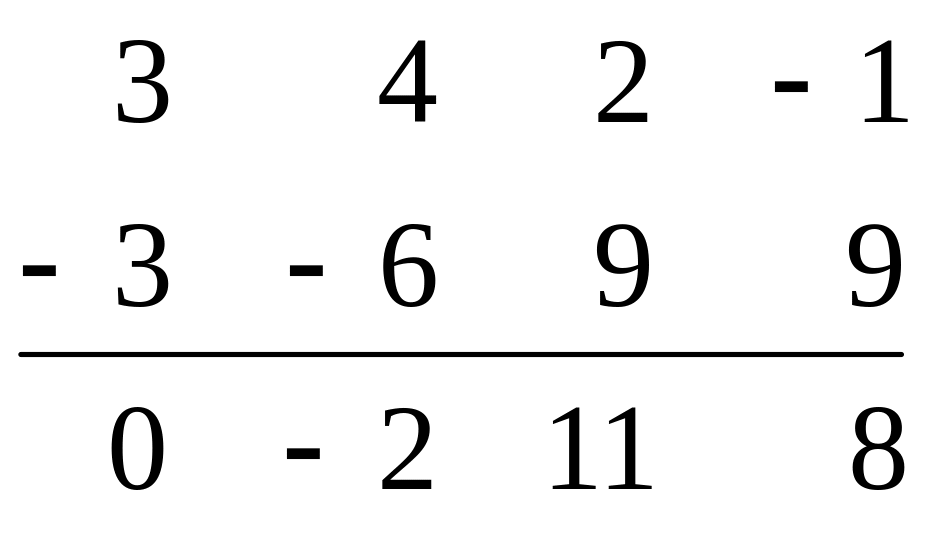
Теперь матрица будет иметь вид:

.

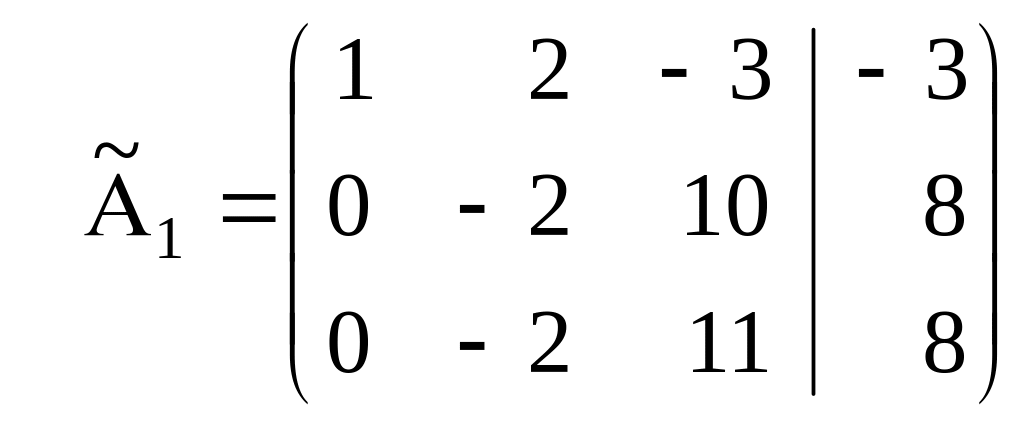Если матрицу будем рассматривать, как систему уравнений, то увидим, что в результате элементарных преобразований получили систему равносильную исходной, причем неизвестная в первое уравнение входит с коэффициентом единица, а из остальных уравнений она исключена.

2. Второй шаг решения (II шаг) состоит в том, что неизвестная исключается из всех уравнений кроме второго, а во второе должна входить с коэффициентом единица.

2.1. Выбираем любую строку, которая еще не была разрешающей, и у которой второй элемент не равен нулю (в нашем примере можно взять, например, вторую строку матрицы ). Эту строку назовем «разрешающая (ведущая) строка второго шага». Второй столбец назовем «разрешающий (ведущий) столбец второго шага», а элемент, расположенный на пересечении разрешающей строки и разрешающего столбца назовем «разрешающий (ведущий) элемент второго шага».

.

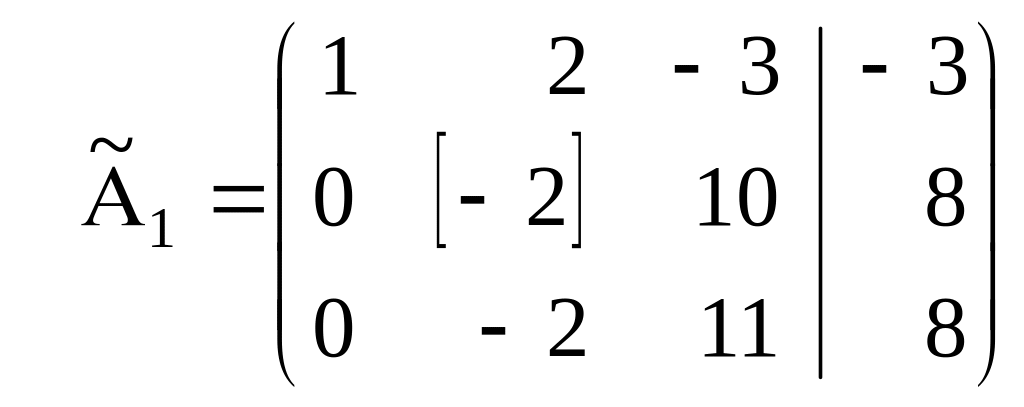
2.2. Разрешающую (вторую) строку делим на разрешающий элемент. Получаем новую строку ( ), которую записываем второй строкой в новой матрице . При этом новая матрица примет вид:

.

2.3. Чтобы найти первую строку матрицы ,ко второй строке матрицы прибавим новую вторую строку из матрицы , предварительно умножив ее на такое число, чтобы во втором столбце оказался ноль. В нашем примере к первой строке матрицы нужно прибавить вторую строку матрицы , умноженную на (-2), получим:

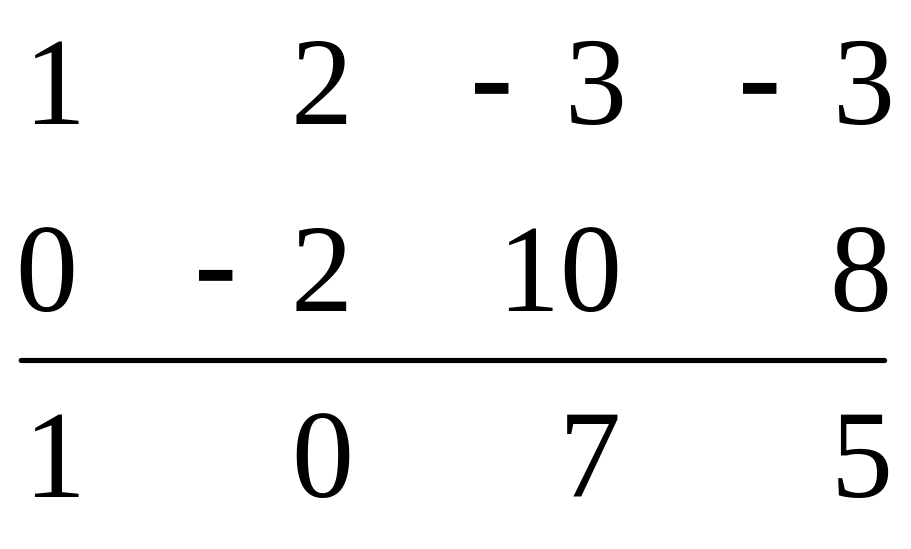
Теперь матрица будет иметь вид:

.

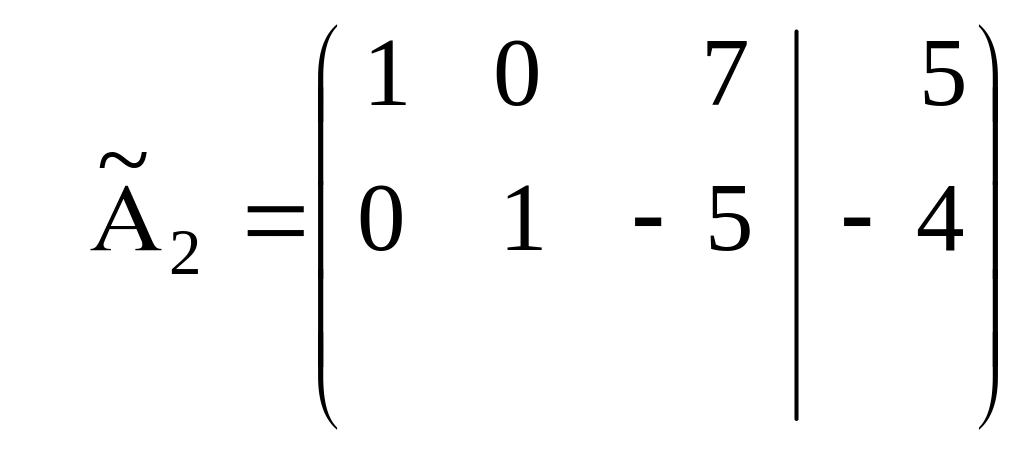2.4. Чтобы найти третью строку матрицы , к третьей строке матрицы прибавим новую первую строку из матрицы , предварительно умножив ее на такое число, чтобы во

втором столбце оказался ноль. В нашем примере ко второй строке матрицы нужно прибавить вторую строку матрицы , умноженную на (+2), получим:

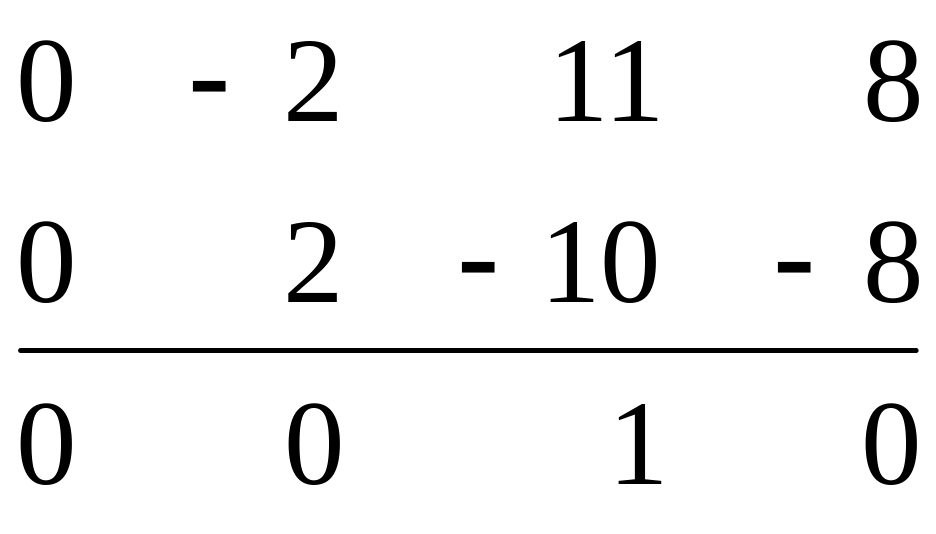
Теперь матрица будет иметь вид:

.

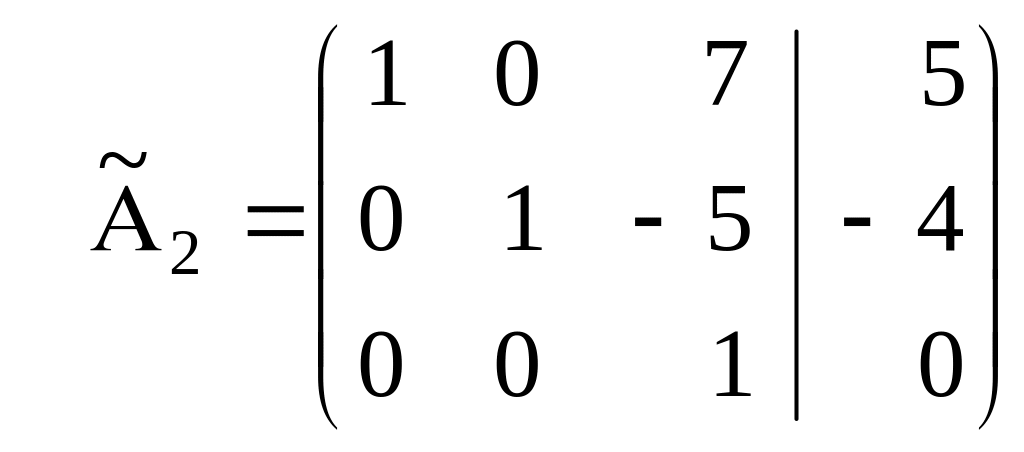Если матрицу рассматривать, как систему уравнений, то увидим, что в результате элементарных преобразований получили систему равносильную исходной, причем неизвестная исключена из всех уравнений кроме первого а из всех уравнений кроме второго.