Выпуклые множества
Пусть точки
и числа
,
тогда линейную комбинацию этих точек
можно записать
в виде точки
.
8.1. Линейную комбинацию точек будем называть выпуклой , если ее коэффициенты неотрицательны и их сумма = 1.
-
выпукла
.
8.2. Отрезком между двумя данными точками будем называть множество всех таких точек, которые являются выпуклыми линейными комбинациями двух данных точек. Две данные точки при этом назовем концами отрезка .
8.3. Выпуклым множеством будем называть такое множество точек, которое вместе с двумя своими любыми
точками содержит и их любую выпуклую комбинацию (т. е. содержит весь отрезок между ними).
Например, круг – выпуклое множество, а окружность - нет. Треугольник является выпуклым множеством.
Крайними (угловыми) точками выпуклого множества будем называть такие точки, которые нельзя представить
в виде выпуклой комбинации других точек этого множества.
Например, вершины треугольника является его крайними точками , а все точки окружности – крайние точки круга.
Любую точку выпуклого множества можно представить в виде выпуклой комбинации его крайних точек.
Выпуклое множество будем называть многогранником или многогранным множеством, если оно содержит конечное количество крайних точек.
8.7. Система линейных ограничений, заданных уравнениями и (или) неравенствами, является выпуклым множеством.
- Выпуклое множество.
Пусть на оси ОХ даны две точки:
Тогда любая
,
делит отрезок
в отношении
, при этом
или
.
Если коэффициенты при
и
обозначить
то получим: любая точка
отрезка
имеет координату х
, удовлетворяющую условиям
.
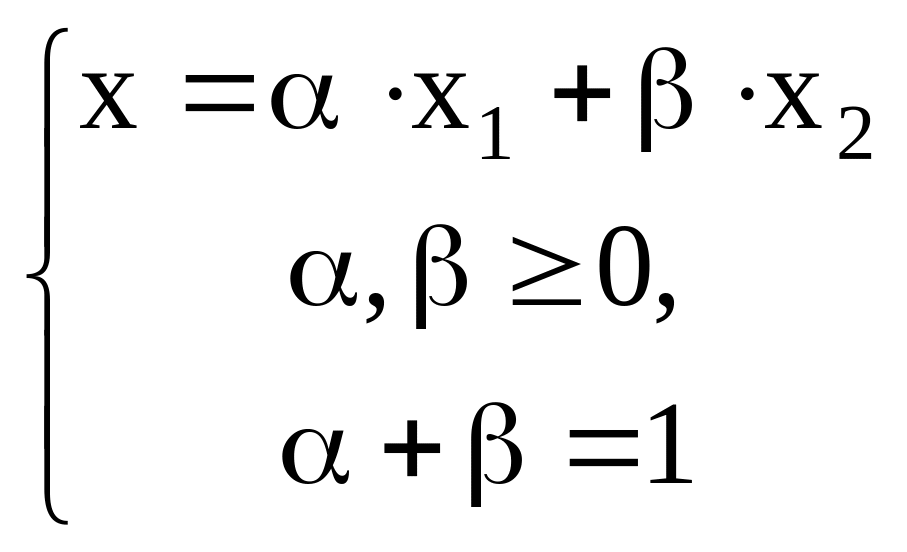Отсюда следует, что координата любой
точки отрезка является линейной
комбинацией координат его концов, при
этом коэффициенты этой линейной
комбинации неотрицательны и в сумме
равны единице.
Определение Точку
будем называть выпуклой комбинацией
точек
,
если координата
есть линейная комбинация координат
точек
,
причем коэффициенты этой линейной
комбинации неотрицательны и в сумме
равны единице.
Следствие Отрезок между двумя точками можно рассматривать как множество всех точек, каждая из которых является выпуклой комбинацией его концов.
Пусть теперь даны две точки в n
- мерном пространстве
:
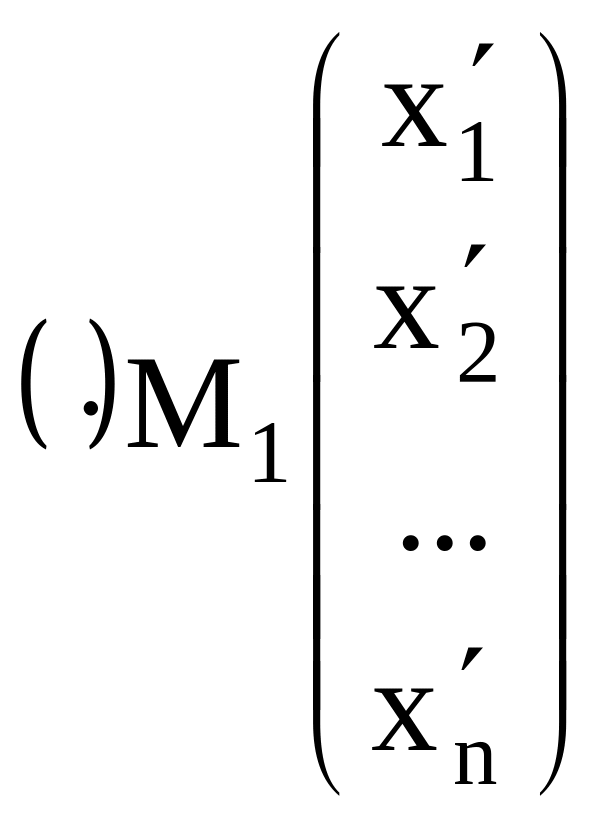и
.
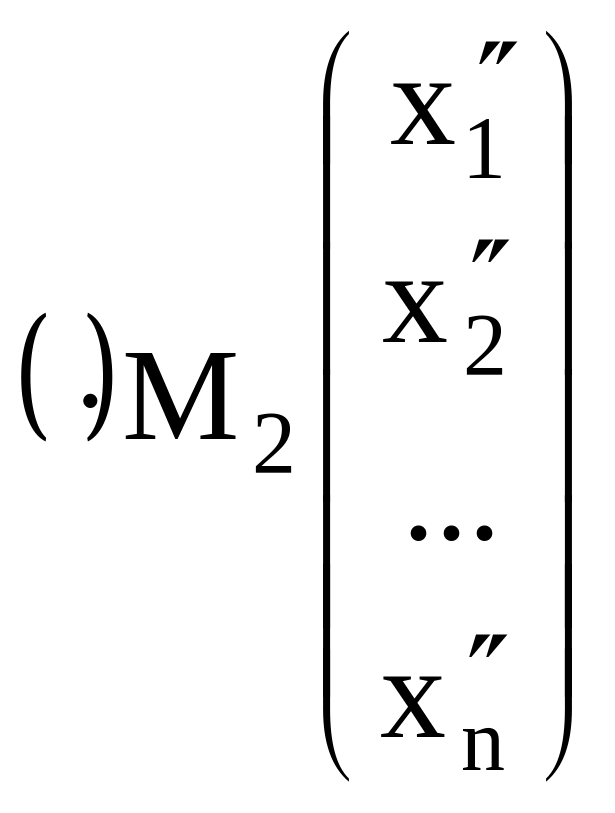Определение Точку
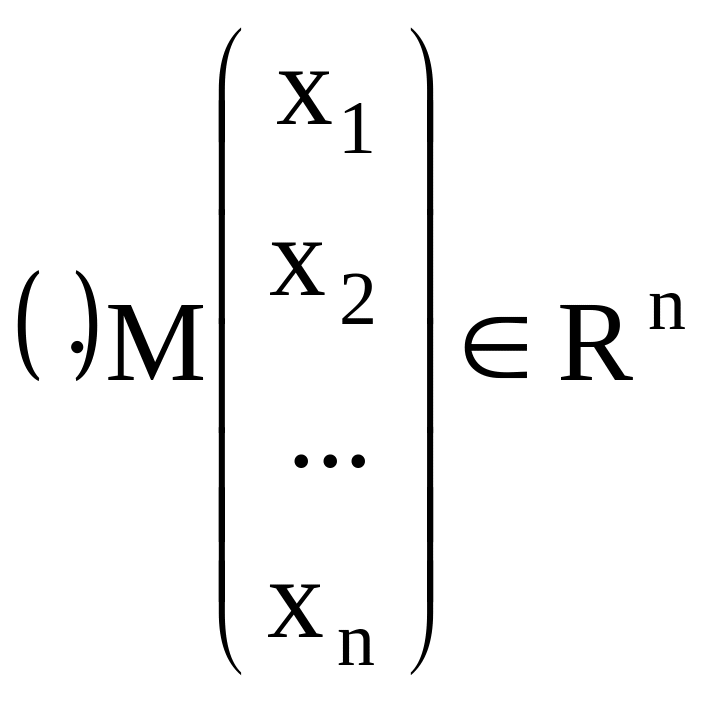будем называть выпуклой комбинацией
точек
,
если
.
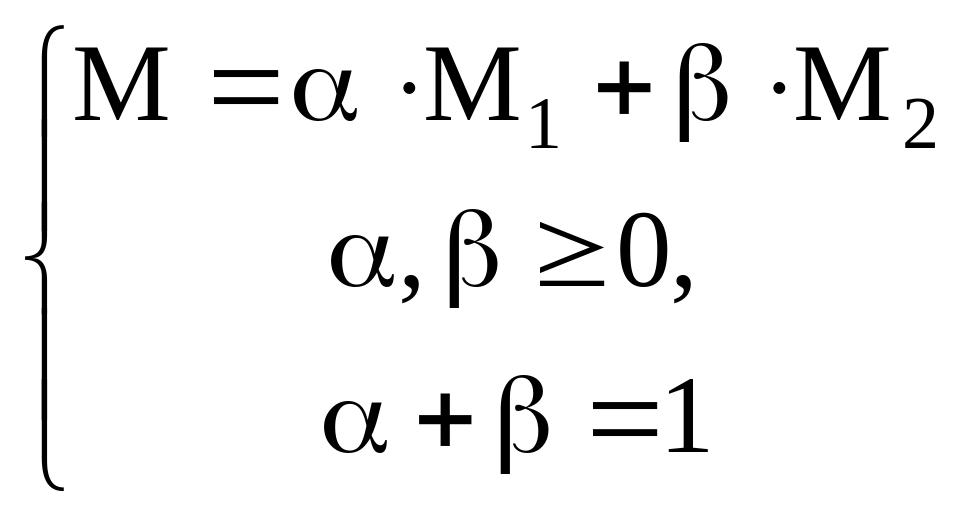Определение Отрезком меду двумя точками в будем называть множество всех точек, являющихся их выпуклыми комбинациями.
Пусть точки и числа , тогда линейную комбинацию этих точек можно записать
в виде точки .
8.1. Линейную комбинацию точек будем называть выпуклой , если ее коэффициенты неотрицательны и их сумма = 1.
- выпукла .
8.2. Отрезком между двумя данными точками будем называть множество всех таких точек, которые являются выпуклыми линейными комбинациями двух данных точек. Две данные точки при этом назовем концами отрезка .
8.3. Выпуклым множеством будем называть такое множество точек, которое вместе с двумя своими любыми
точками содержит и их любую выпуклую комбинацию (т. е. содержит весь отрезок между ними).
Например, круг – выпуклое множество, а окружность - нет. Треугольник является выпуклым множеством.
Крайними (угловыми) точками выпуклого множества будем называть такие точки, которые нельзя представить
в виде выпуклой комбинации других точек этого множества.
Например, вершины треугольника является его крайними точками , а все точки окружности – крайние точки круга.
Любую точку выпуклого множества можно представить в виде выпуклой комбинации его крайних точек.
Выпуклое множество будем называть многогранником или многогранным множеством, если оно содержит конечное количество крайних точек.
8.7. Система линейных ограничений, заданных уравнениями и (или) неравенствами, является выпуклым множеством.