3. Обращение квадратных матриц

Пусть дана квадратная матрица n -го порядка : .

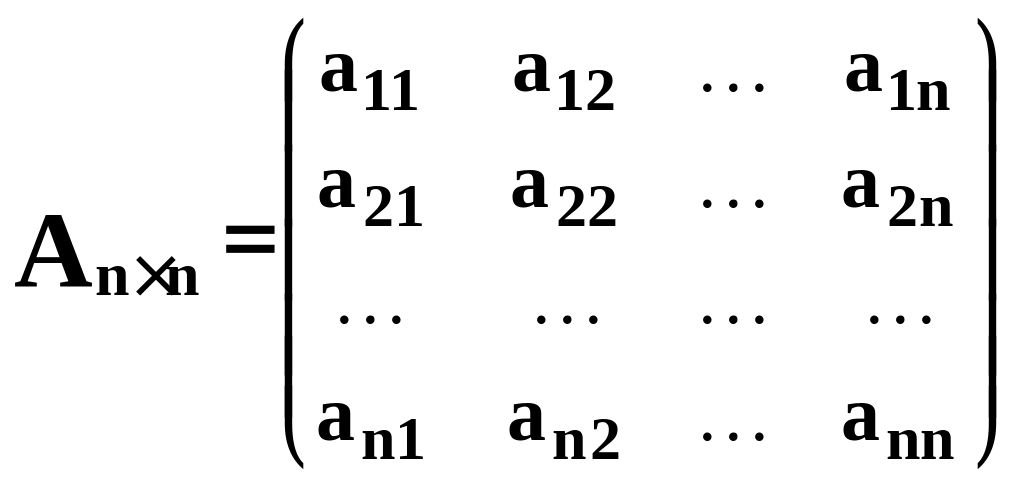3.1. Для того чтобы у квадратной матрицы существовала обратная матрица необходимо и достаточно, чтобы данная матрица была невырождена, при этом обратная матрица будет единственной и ее можно найти по формуле:

.

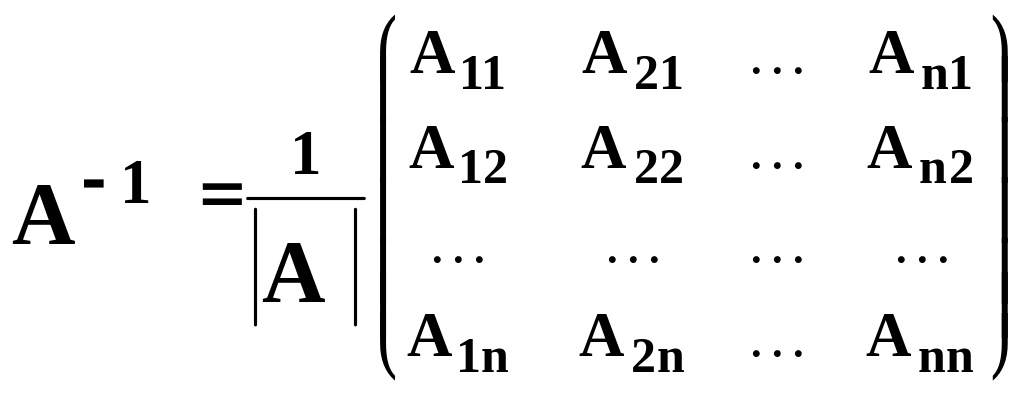Матрицу, расположенную в правой части этой формулы называют присоединенной к данной матрице А. Присоединенная матрица получается в результате замены всех ее элементов своими алгебраическими дополнениями и транспонированием вновь полученной матрицы.

Следовательно, чтобы найти обратную матрицу для данной невырожденной квадратной матрицы, достаточно найти ее присоединенную матрицу и все ее элементы разделить на величину определителя данной матрицы.

2. Невырожденную квадратную матрицу будем называть ортогональной, если при транспонировании получим

обратную ей матрицу. .

Для ортогональной матрицы А справедливы свойства:

3.2.1. .

3.2.2. .

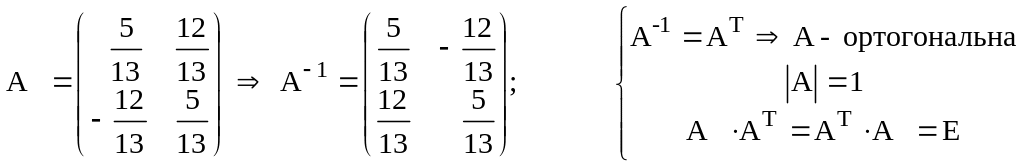
3.2.3. Если матрицы А и В - ортогональны, то А^Т, А^-1, АВ - тоже ортогональны.

3.2.4. Если матрица А ортогональна и симметрична, то .

4. Ранг матрицы

Пусть дана прямоугольная матрица : .

Минором k -го порядка будем называть определитель, полученный из нее после вычеркивания (m-k) строк и (n-k) столбцов.

Минорами первого порядка являются элементы матрицы.

Наибольший порядок минора, который можно составить равен min {m, n}.

Рангом матрицы будем называть наибольший порядок отличного от нуля минора.

Из определения следует, что ранг невырожденной квадратной матрицы n -го порядка равен n, а ранг любой нулевой матрицы равен 0.

Базисными будем называть все миноры, отличные от нуля, порядок которых равен рангу матрицы.

Строки и столбцы матрицы ,входящие в базисный минор, будем называть базисными, а остальные ряды - свободными.

Элементарными преобразованиями матрицы назовем следующие операции:

- транспонирование;

- перестановки параллельных рядов (строк или столбцов);

- вычеркивание нулевого ряда;

- вычеркивание всех кроме одного одинаковых или пропорциональных

параллельных рядов;

- умножение любого ряда на число, не равное нулю;

- прибавление к любому ряду линейной комбинации параллельных рядов.

4.1. Элементарные преобразования не изменяют ранга матрицы.

2. Если ранг матрицы 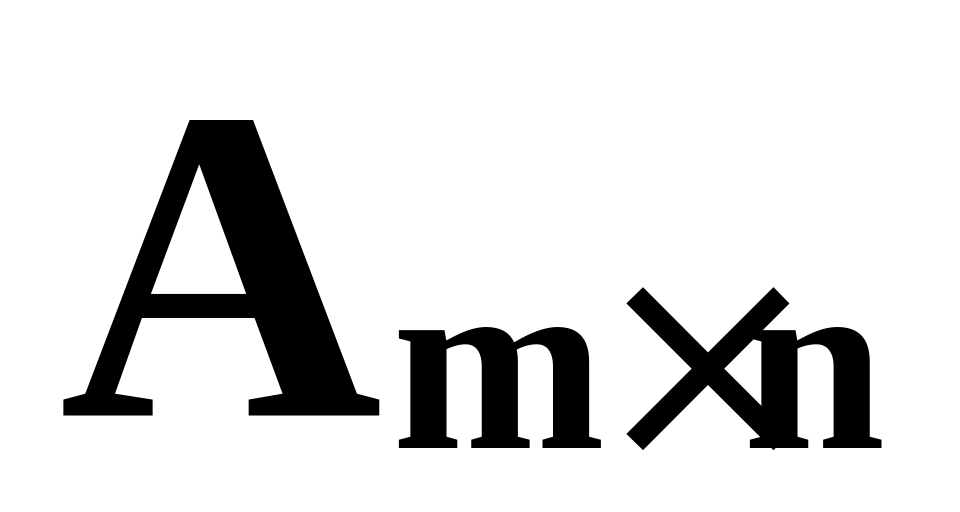равен r, то в ней можно найти ровно r линейно независимых строк

и столько же линейно независимых столбцов, при этом .

4.3. Любой ряд матрицы можно представить в виде линейной комбинации параллельных базисных рядов.

4.4. Для того чтобы определитель квадратной матрицы был равен нулю, необходимо и достаточно,

чтобы его строки (либо столбцы) были линейно зависимы.

5. Системы линейных уравнений

Пусть дана система, содержащая m линейных уравнений с n неизвестными:

5.1.

Введем следующие обозначения.

5 .2. ,

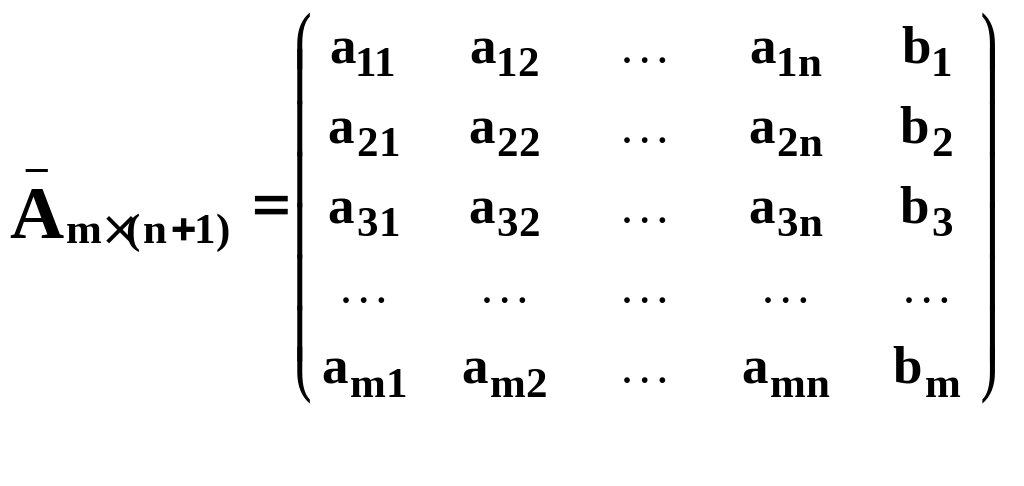
- матрица системы - ее расширенная матрица.

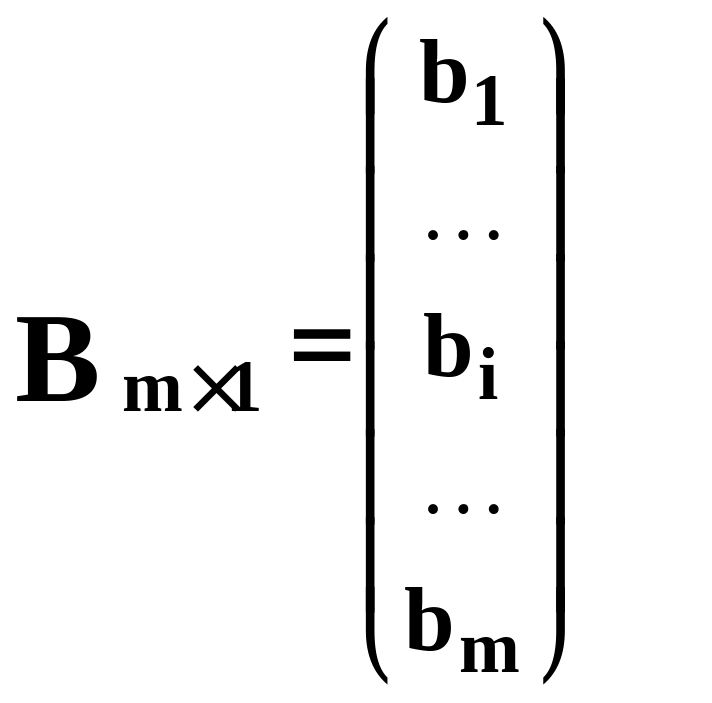- столбец свободных членов. 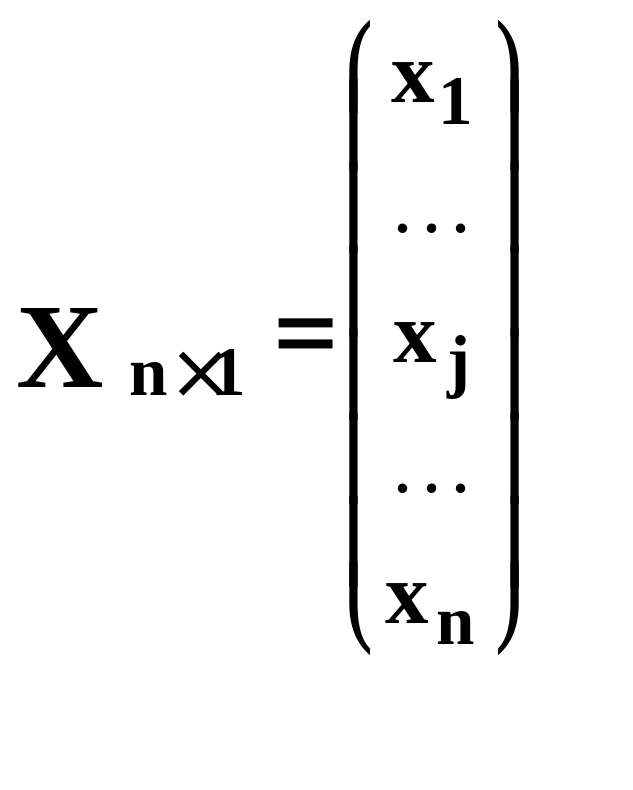- столбец неизвестных.

Если столбец свободных членов нулевой, то систему называют однородной.

Расширенная матрица 5.2. полностью задает систему 5.1.

Систему 5.1. можно задать также в виде матричного уравнения:

5.3. .

5.3.1. Система 5.1. и матричное уравнение 5.3. эквивалентны.

5.3.2. Теорема Кронекера-Капелли

Для того чтобы система 5.1. была разрешима, необходимо и достаточно, чтобы ранг расширенной

матрицы был равен рангу матрицы системы.

5.3.3. Если , то система имеет единственное решение.

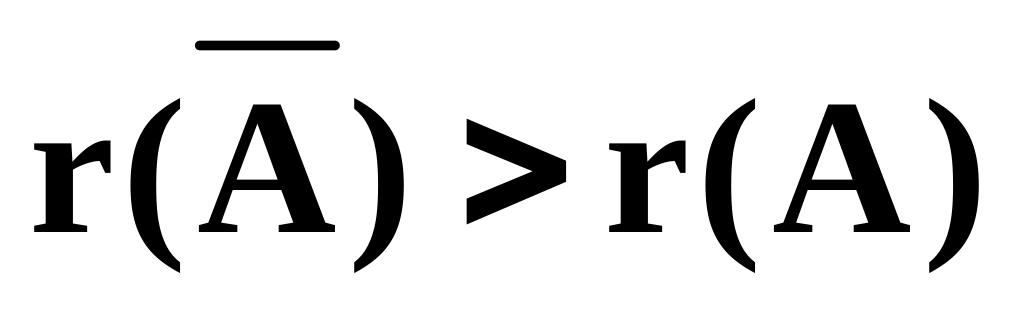4. Если , то система не имеет решений.

5.3.5. Однородная система всегда разрешима, причем линейная комбинация векторов, являющихся решениями

однородной системы тоже является ее решением.

5.3.6. Если , то система имеет бесчисленное множество решений, при этом (n - k)

неизвестных могут принимать произвольные значения (их называют свободными), а остальные

k неизвестных (называемых базисными) можно представить в виде линейной комбинации свободных.