2. Определители

2.1. Определители второго порядка

Пусть дана квадратная матрица второго порядка:

.

Определителем второго порядка будем называть числополученное из квадратной матрицы второго порядка по формуле:

.

Другие обозначения определителя:

.

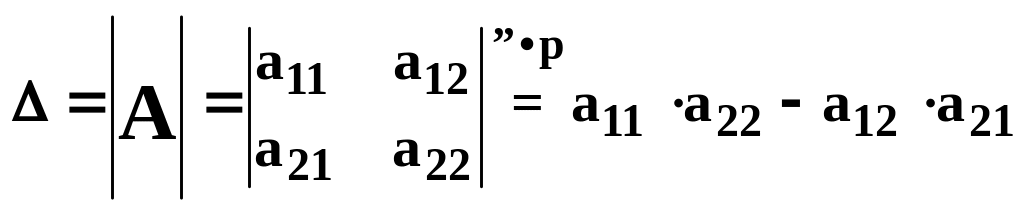2.2. Определители третьего порядка

Пусть дана квадратная матрица третьего порядка: .

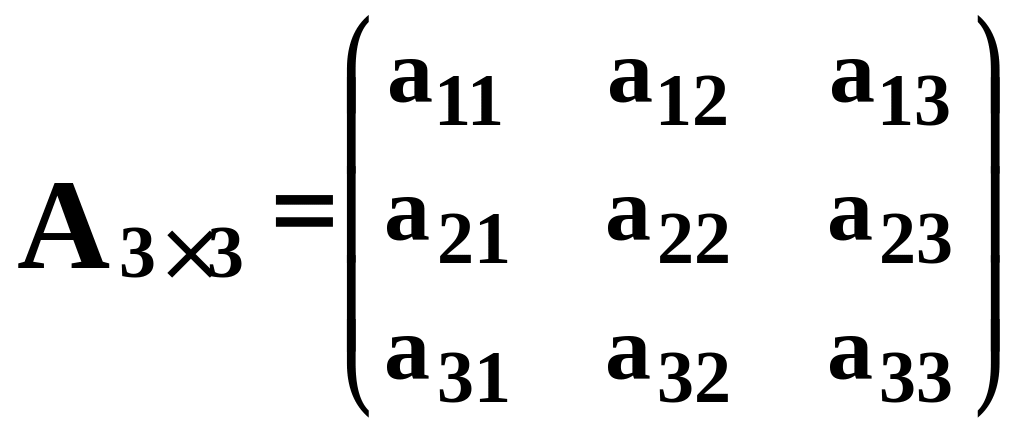Определителем третьего порядка будем называть число, полученное из квадратной матрицы третьего порядка по формуле:

Другие обозначения:

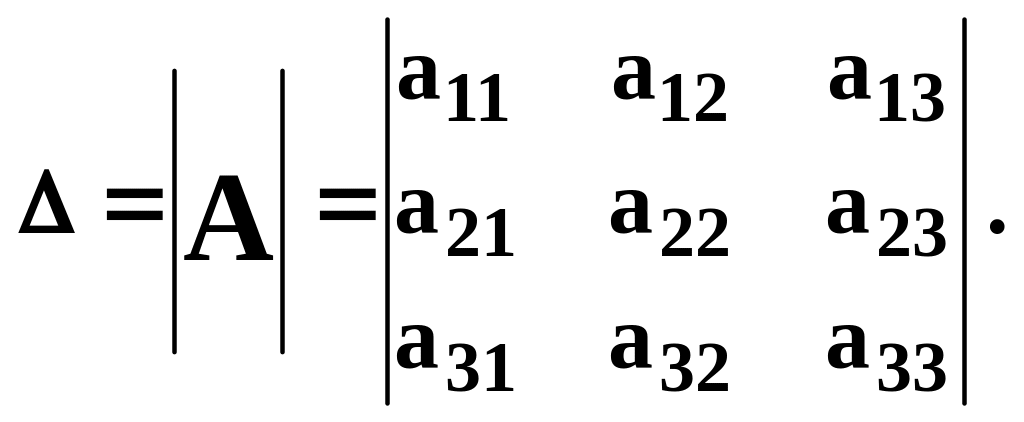
Минором элемента a_ij (M_ij) будем называть определитель, полученный из данного после вычеркивания i-ой строки и

j-го столбца.

Пример:

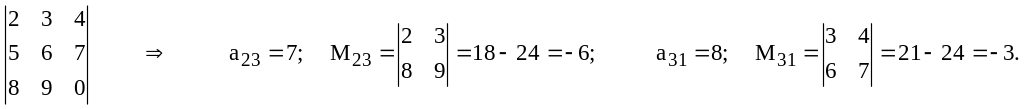
Из определения минора следует:

- минор это тоже определитель, только его порядок на единицу меньше, чем у данного;

- минор определителя второго порядка это элемент данного определителя, его называют также определителем первого порядка.

Алгебраическим дополнением элемента a_ij (A_ij) будем называть минор этого элемента, умноженный на (-1)^i+j. .

Свойства:

2.2.1. Транспонирование матрицы не меняет величину ее определителя.

Следствие: все свойства, справедливые для строк определителя, будут справедливы также и для его столбцов.

2.2.2. Если две строки поменять местами, то абсолютная величина определителя не изменится,

а знак поменяется на противоположный.

2.2.3. Если все элементы строки умножить на одно и то же число, то определитель умножится на это же число.

Следствие: если все элементы строки содержат общий множитель, то его можно вынести за знак определителя.

2.2.4. Определитель равен нулю в следующих случаях: - содержит нулевую строку;

- содержит одинаковые строки;

- содержит пропорциональные строки.

2.2.5. Если к строке прибавить линейную комбинацию других строк, то величина определителя не изменится.

Следствие: если к строке прибавить другую строку (или вычесть ее), то величина определителя не изменится.

2.2.6. Определитель можно вычислить, как сумму произведений всех элементов какой-нибудь строки на свои

алгебраические дополнения.

Этот способ вычисления называют разложением определителя по строке.

2.2.7. Сумма произведений всех элементов строки на алгебраические дополнения соответствующих элементов

другой сроки всегда равна нулю.

2.2.8. Определитель произведения двух квадратных матриц равен произведению их определителей.

Пример

2.3. Определители n -го порядка

Пусть дана квадратная матрица n -го порядка: .

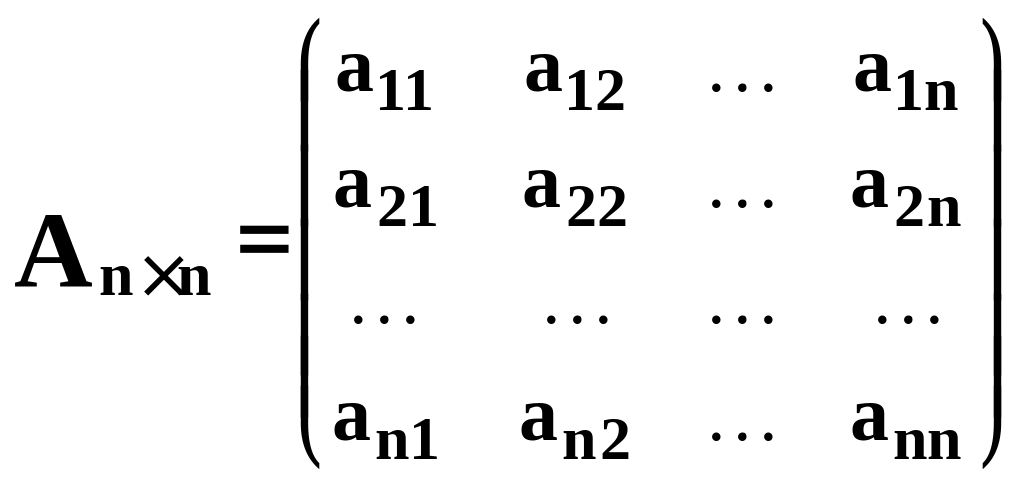Определителем n -го порядка будем называть число полученное изквадратной матрицы n -го порядка,равное сумме произведений всех элементов любой ее строки ( или столбца ) на свои алгебраические дополнения.

Другие обозначения для определителя n -го порядка:

.

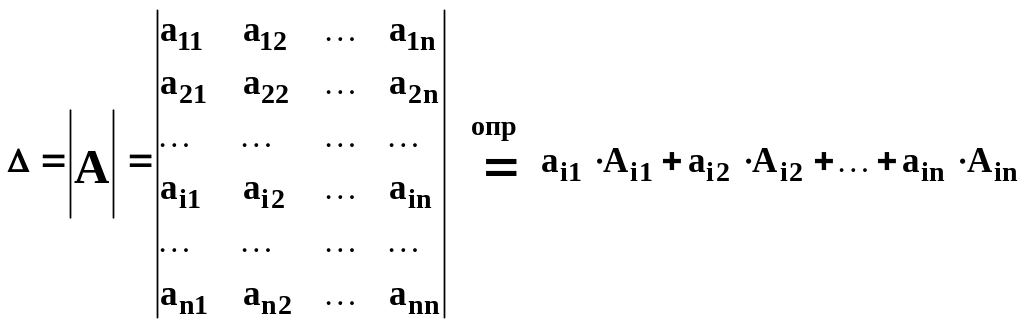Все понятия и свойства, сформулированные в 2.2.1 - 2.2.8 для определителей третьего порядка, справедливы также для определителей любого порядка .

Квадратную матрицу будем называть невырожденной, если ее определитель не равен нулю.

Квадратную матрицу будем называть вырожденной (особенной), если ее определитель равен нулю.