5. Комплексные числа
Дайте определение и приведите пример комплексно-сопряженных чисел. Докажите, что для комплексных чисел
,
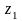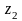справедливы равенства: а)
,
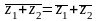б)
.
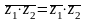Комплексное число Z обозначается символом a+ib, где а и в – действительные числа, называемые соответственно действительной частью и мнимой частью комплексного числа; символ i, определяемы условием i*i=-1, называется мнимой единицей. Комплексное число а-ib называется сопряжённым с числом z=a+ib и обозначается z’
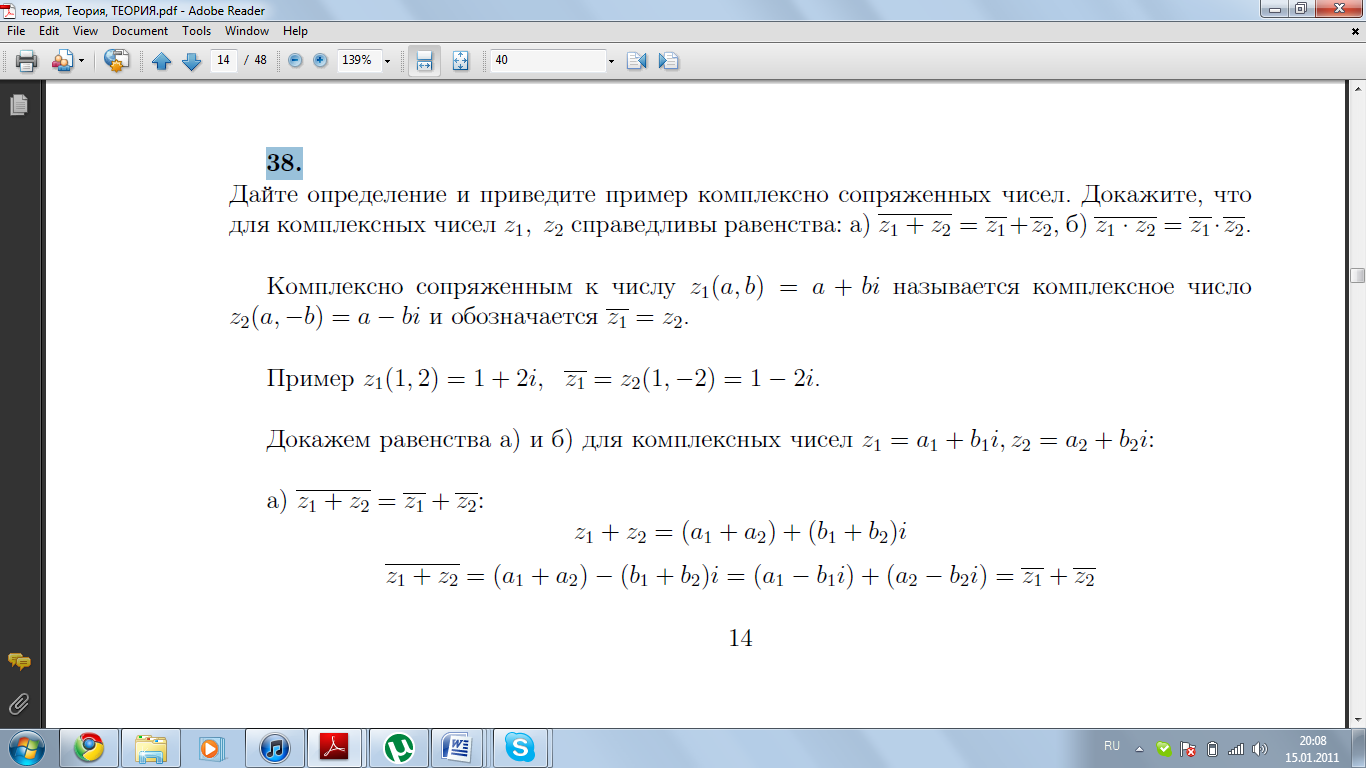
Изобразите на плоскости комплексные числа
,
,
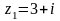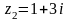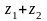и
.
Z=a+bi, по оси х откладываете а, по оси у откладываете в.
Дайте определение модуля и аргумента комплексного числа
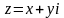и укажите способ их нахождения.
Запишите в тригонометрической форме числа
,
.
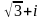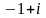Найдите модуль комплексного числа
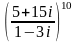
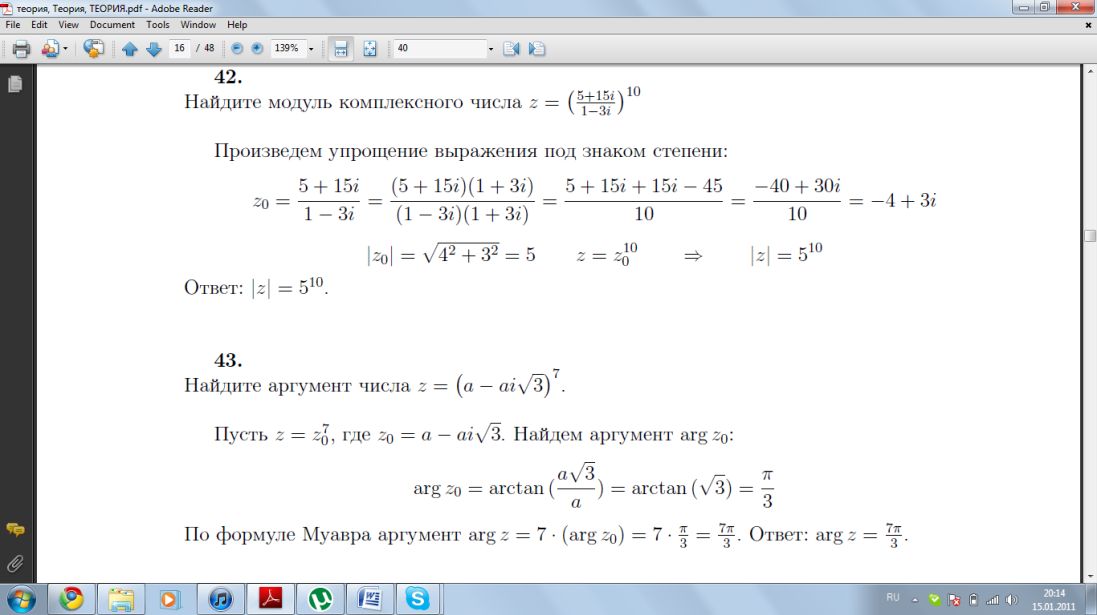
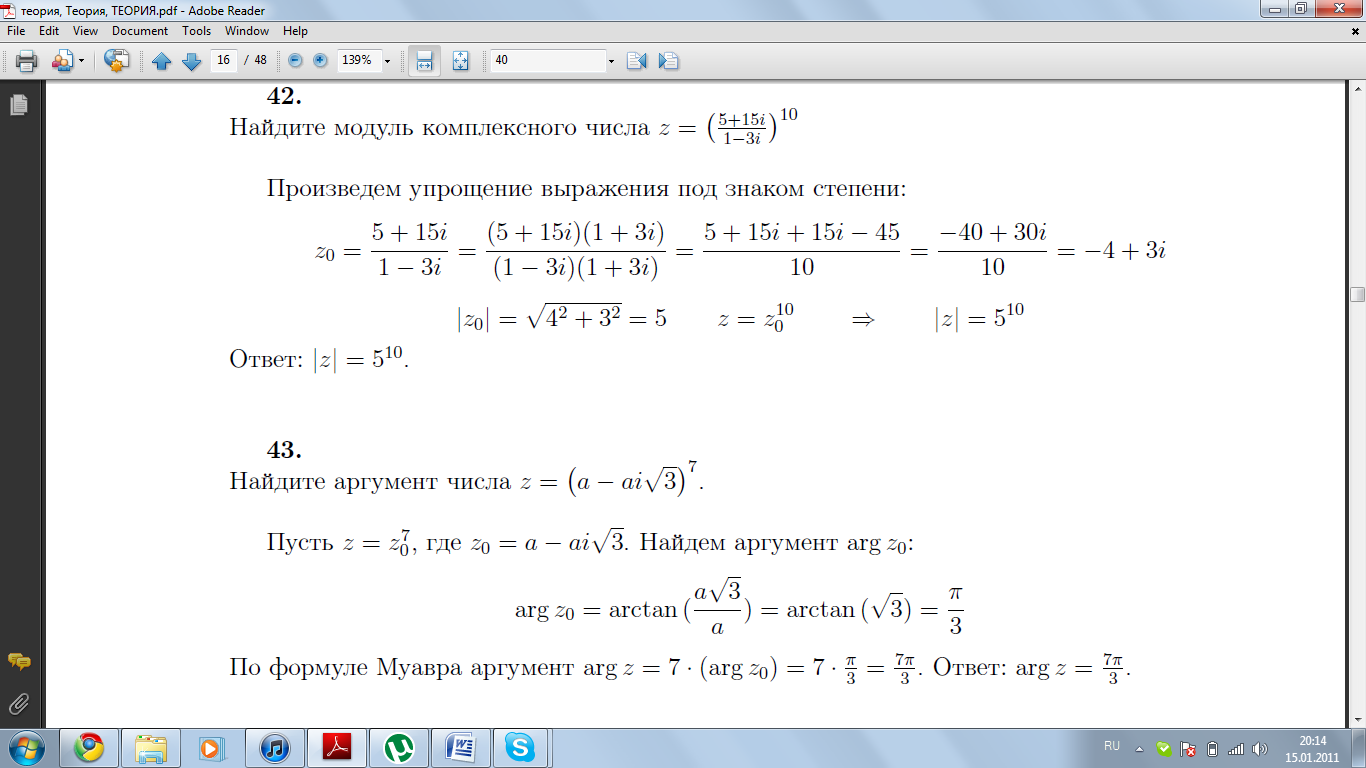
Найдите аргумент числа
.
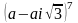Используя формулу Муавра, вычислите
.
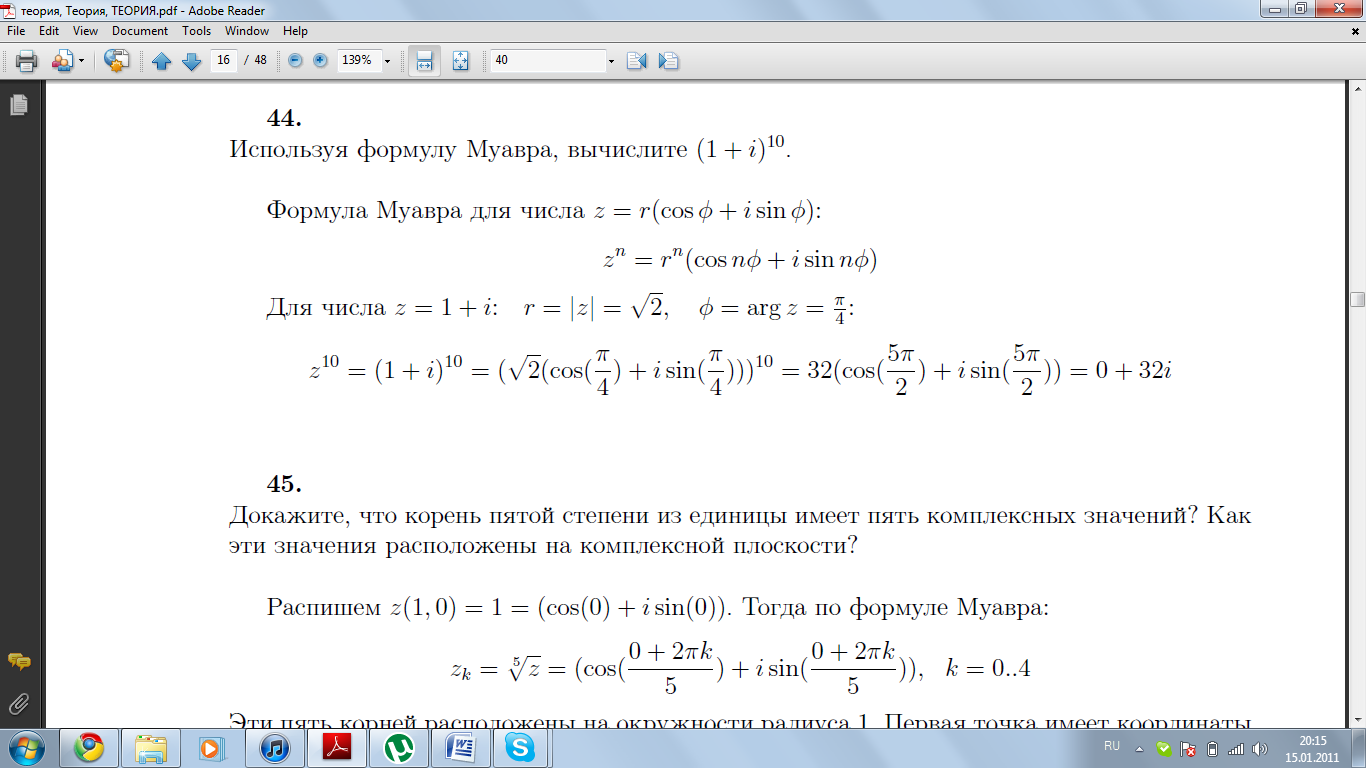
Докажите, что корень пятой степени из единицы имеет пять комплексных значений. Как эти значения располагаются на плоскости?
Сформулируйте основную теорему алгебры комплексных чисел.
Многочлен n-ой степени имеет на комплексной плоскости ровно n нулей (с учетом их кратности).
Или: Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.
Может ли квадратное уравнение в области комплексных чисел: а) не иметь корней; б) иметь более двух корней? Ответ обоснуйте.
а)б) - не верно.
Опираясь на основную теорему алгебры комплексных числел, любое квадратное уравнение(уравнение второй степени) в области комплексных чисел имеет ровно 2 комплексных корня (в некоторых случаях комплексные корни могут быть действительными, если они лежат на действительной оси).
Решите уравнение в области комплексных чисел: а)
;
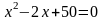б)
;
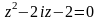в)
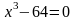
Многочлен степени 4 с действительными коэффициентами имеет корень
.
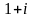Докажите, что корнем этого многочлена
является число
.
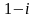6. Линейные операторы в пространстве
Дайте определение линейного оператора. Проверьте линейность оператора, переводящего вектор
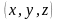в вектор
.
Дайте определение матрицы линейного оператора в данном базисе. Приведите пример.
Рассмотрим базис (e1, ..., en) в пространстве Rn.
Линейный оператор A : Rn → Rn : Ax = y. Разложим по базису x = x1e1+...+xnen, где
(x1, ..., xn) - координаты вектора x в указанном базисе. Тогда в силу линейности оператора
A получим: Ax = x1Ae1 + ... + xnAen
Разложим элементы Aei, i = 1..n по указанному базису:Ae1 = a11e1 + a21e2 + ... + an1en,
...
Aen = a1ne1 + a2ne2 + ... + annen,
Матрицей линейного оператора A в указанном базисе (e1, ..., en) называется матрица, составленная из коэффициентов разложения
A =a11 ... a1n
... ... ...
an1 ... ann
Пример: Линйный оператор отражения от плоскости Oxy: A(x, y, z) = (x, y,−z) имеет
Матрицу A =1 0 0
0 1 0
0 0 −1
Как изменяется матрица линейного оператора при переходе от одного базиса к другому? Ответ проиллюстрируйте на примере.
Теорема (о переходе к другому базису) Пусть Ae - матрица линейного оператора A в базисе E = (e1, ..., en). Пусть Af - матрица линейного оператора A в базисе F = (f1, ..., fn).
Тогда матрицы связаны соотношением:
Af = P−1e→fAePe→f
где Pe→f - матрица перехода от базиса E к базису F: F = EPe→f .
Найдите матрицу преобразования
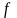пространства
в стандартном базисе: а)
- поворот на угол
;
б)
- симметричное отражение векторов
относительно прямой
.
a) A =cos α −sin α
sin α cos α
b) A =0 1
1 0
Дайте определение собственных значений и собственных векторов линейного оператора. Приведите пример.
Число λ называется собственным значением (собственным числом) линейного оператора A , если ∃x не= 0 : Ax = λx
x не= 0 называется собственным вектором линейного оператора A, отвечающим собственному числу λ.
Пример: f(x, y) = (2x, 2y) имеет собственное значение λ = 2, так как для любого вектора v(a, b) : f(v) = 2v.
Как связаны между собой собственные значения линейных операторов и
?
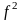Ответ обоснуйте.
Пусть λ - собственный вектор f так, что f(x) = λx. Тогда f2x = f(f(x)) = f(λx) = λf(x) = λ2x
Это означает, что если λ - собственное значение f, то λ2 - собственное значение f2.
Как связаны между собой собственные значения линейных операторов и
?
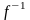Ответ обоснуйте.
Пусть λ - собственный вектор f так, что f(x) = λx. Тогда x = f−1(f(x)) = f−1(λx) = λf−1(x)
Получили: x = λf−1(x) ⇒1/λ*x = f−1(x)
Это означает, что если λ - собственное значение f, то 1/λ - собственное значение f−1.
Могут ли все собственные значения ненулевой матрицы быть равными 0? Ответ обоснуйте для квадратных матриц порядка
.
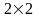Рассмотрим матрицу A =a b c d
. Запишем характкристический многочлен и приравняем его к 0, чтобы найти собственные значения матрицы:
(a − λ)(d − λ) − bc = 0
Предположим, что λ = 0 - корень характеристического уравнения, то есть λ = 0 -
собственное значение матрицы A. Тогдa, подставив λ = 0 в уравнение получим условие:
ad = bc.
Как только ad = bc, то λ = 0 - корень уравнения. Если же ad = bc, то λ = 0 не будет являться корнем уравнения. Поэтому подставим это уравнение в хар. уравение и упростим
его: (a − λ)(d − λ) − bc = 0
ad − bc − (a + d)λ + λ2 = 0
λ2 − (a + d)λ = 0
(λ − (a + d))λ = 0
Мы видим, что, как только λ = 0 - собственное значение ad = bc тогда λ = a+d – тоже собственное значение. Предположим, что a = −d. Тогда оба собственных значения будут равны 0.
Получены условия нулевых собственных значений матрицы 2 × 2:1. ad = bc, 2. a = −d