
- •18 Статически неопределимые задачи при кручении.
- •19.Расчёт винтовых цилиндрических пружин с малым шагом витка на прочность. Деформация винтовых цилиндрических пружин.
- •Часть 2.
- •21.Построение эпюр в консольной балке.Диф зависимости.
- •2 3. Определение касательных напряжений при изгибе (формула Журавского)
- •24. Главные напряжения при изгибе.
- •25.Подбор сечений и проверка прочности балок.
- •26.Траектория главн напр.Потенц. Энергия при изгибе.
- •28.Пример определения перемещений в балках
- •22.Определение нормальных напряжений при чистом изгибе
- •29.Графоаналитич. Метод определения перемещений в балках.
- •30.Простейшие статически неопределимые балки. Порядок расчета.
- •50. Определение деформаций и перемещений в толстой трубе. Понятие о расчёте составных цилиндров. Усл прочн.
- •51. Учёт сил инерции при действии динамических нагрузок. Напряжение при ударе.
- •52. Проддольный поперечный и скручивающий удар. Понятие об усталостной прочности
- •7. Статически неопределимые задачи при растяжении, сжатии: а) статически неопределимый брус; б)температурные напряжения; в)стержневые системы.
- •45.Определение максимального прогиба при внецентренном сжатии гибкого стержня. Условие прочности.
- •46.Понятие о расчёте тонкостенных оболочек. Определение напряжений в осесимметрических оболочках по безмоментной теории.
- •47.Определение напряжений в сферическом и цилиндрическом сосудах. Условие прочности для тонкостенных сосудов.
- •48.Понятие о расчёте толстостенных труб под действием осесимметрической нагрузки. Напряжения в толстостенной трубе. Задача Ляме.
1.Сопромат-наука, изучающая инженерные методы расчёта конструктивных элементов, сооружений, конструкций, машин и рд на прочтность, жёсткость, и устойчивасть.
- Прочность – способность не разрушаться под нагрузкой;
- Жёсткость – способность незначительно деформироваться под нагрузкой;- Выносливость – способность долгое время выдерживать переменные нагрузки; - Устойчивость – способность сохранять первоначальную форму упругого равновесия;
В 1660г Гук вывел линейную зависимость между деформацией и нагрузкой.
1826-навье- первый учебник по сопромату и ввел поняимя напряжения и деформации.
Виды конструктив элементов:
-Брус-элемент, поперечное сечение которого мало по сравнению с его длиной .Линия, соединяющая центр тяжести поперечного сечения называется осью бруса. Сечение перпендикулярное оси называется поперечным.
-пластинка и оболочка
-массив(все 3 размера одного порядка)
Расчетная схема конструкции - его упрощенная схема, освобожденная от несущественных в данной задаче особенностей.
Силы классифицируют на: внутренние и внешние
2.Основные гипотезы и допущения 1. Идеальноупругое тело(сплошное однородное изотропное тело)
2. В ненагруженном состоянии тело свободно от сил любой природы.
3. Принцип начальных размеров(перемещения точек тела малы по сравнению с его размерами
4.если нагрузка не превышает опред величины, то тело считают линейно деформированным.
5. Принцип независимости действия сил принцип суперпозиции(суммированное воздействие сил равно сумме действия каждой силы в отдельность и не зпвисит от порядка их приложения.)
6.Гипотиза плоских сечений(гипотиза Бернулли – плоские сечения до приложения сил остаются прямыми и плоскими и после деформации)
7.Принцип Сеит-Венана(х-р распределения напряжения по сечению не зависти от способа напряжения в местах, удалённых от приложения нагрузки)
3.Понятие
о напряжениях,перемещениях и
деформациях.внутр силы и их опр.
Меру
интенсивности внутренних сил называют
напряжением.
![]() Нормальное напряжение – проекция
вектора полного напряжения на нормаль
обозначается через σ.
Нормальное напряжение – проекция
вектора полного напряжения на нормаль
обозначается через σ.
![]() ,
где Е – модуль упругости I рода, ε –
линейная деформация Под действием
внешних сил твердые тела изменяют свою
геометрическую форму, то есть деформируются.
В результате действия внешних сил в
теле возникают внутренние силы. Внутренняя
сила — силы взаимодействия между частями
одного тела, возникающие под действием
внешних сил.Внутренние силы являются
самоуравновешенными, поэтому они не
видны и не влияют на равновесие тела.
Определяют внутренние силы методом
сечения.Порядок определения сил:1тело
разделяют на 2 части-2. отбрасывает одну
стороу- 3.заменяем действие отброшенной
части реакциями, которые и явл внутр
силами.-4.уравновешиваем рассм част и
опред внутр силы. 1-4 Метод РОЗУ.
,
где Е – модуль упругости I рода, ε –
линейная деформация Под действием
внешних сил твердые тела изменяют свою
геометрическую форму, то есть деформируются.
В результате действия внешних сил в
теле возникают внутренние силы. Внутренняя
сила — силы взаимодействия между частями
одного тела, возникающие под действием
внешних сил.Внутренние силы являются
самоуравновешенными, поэтому они не
видны и не влияют на равновесие тела.
Определяют внутренние силы методом
сечения.Порядок определения сил:1тело
разделяют на 2 части-2. отбрасывает одну
стороу- 3.заменяем действие отброшенной
части реакциями, которые и явл внутр
силами.-4.уравновешиваем рассм част и
опред внутр силы. 1-4 Метод РОЗУ.
8. Механические характеристики определяются следующими факторами:веществом, его структурой и свойствами;конструктивными особенностями элемента, т. е, размерами, формой, наличием концетраторов, состоянием поверхности;условиями при нагружении: температурой, скоростью, повторяемостью нагрузки и др. По диаграмме растяжения оцениваются механическиехарактеристики материала.
Д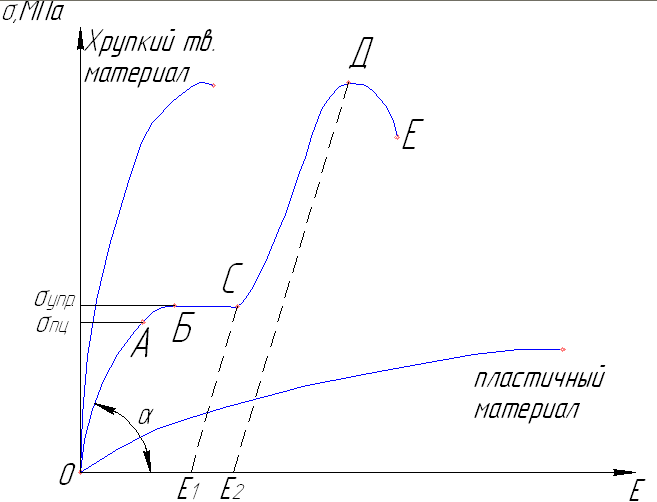 еформация
рассматривается для упругопластичного
материала (малоуглеродистая сталь).
еформация
рассматривается для упругопластичного
материала (малоуглеродистая сталь).
т.
А – предельпропорциональности
![]() ;т.
В – предел упругости
;т.
В – предел упругости
![]() ;т.
С – предел текучести
;т.
С – предел текучести
![]() ;т.
D
– временный предел прочности;т. Е –
разрушение образца.
;т.
D
– временный предел прочности;т. Е –
разрушение образца.
Характеристики материалов:
- Твёрдость;
- Хрупкость;
- Пластичность.
9.Стат моменты.Моменты инерциии сечения.изм моментов инерции при парал переносеСтатические моменты поперечного сечения используют при определении положения его центра тяжести. Рассмотрим сечение произвольной формы площадью А в осях координат x, y и выделим вокруг произвольной точки сечения с координатами x и y элементарную площадку dA, тогда статические моменты Sx и Sy относительно осей x и y определяются:
Sx=A∫ydA, (м3)
S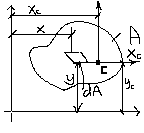 x=A∫хdA,
(м3)
1рис.
x=A∫хdA,
(м3)
1рис.
Статическим моментом сечения относительно какой-либо оси называется сумма произведений элементарной площадки dA на расстояние ее до рассматриваемой оси, взятая по всей площади сечения А. Размерность статических моментов – м3, см3. Координаты элементарных площадок dA могут быть «+» или «-» или =0 => статический момент сечения может быть«+» или «-» или =0. Если статический момент относительно некоторой оси =0, то эта ось проходит ч/з центр тяжести сечения и наз. центральной осью, предыдущие формулы можно представить в виду:
Sx=yc∙A Sy=xc∙AГде xc и ус координаты центра тяжести С площадки А. Для сложных или составных сечений координаты центра тяжести определяются
xc=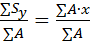
yc=
. Осевым моментом инерции сечения относительно какой-либо оси наз-ся сумма произведений элементарной площадки dA на квадрат расстояния ее до соответствующей оси, взятая по всей площади А.
Ix=A∫y2dA, (м2),Iy=A∫x2dA, (м2)
10) Определение моментов инерции для круглого,трубчатого, прмоуг и треуг сеченияПредставим, что сечение разделено на множество элементарных площадок dA, координаты которых x и y. Моменты инерции сечения относительно осей x и y: Iх=(А)∫у2dА, Iу=(А)∫х2dА. Центробежный момент инерции: Iху=(А)∫хуdА. Зависимость между осевыми и полярными моментами инерции: Iр=Iх+Iу - сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения этих осей. Центральный момент инерции — момент относительно осей, проходящих через центр тяжести сечения. Прямоугольное сечение имеет 2 оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон. Главный центральный момент инерции относительно оси x: Iх=(А)∫у2dА. Элементарную площадка dA - полоска во всю ширину сечения толщиной dy, значит dA=b*dy. Проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от —h/2 до +h/2, получим: Iх=bh3/12. Аналогично относительно оси y:Круглое сечение. Для круга главные центральные моменты инерции относительно осей x и y равны между собой: Iх=Iу. Из равенства Iр=Iх+Iу получаем Iр=2Iх=2Iу, I=Ix=Iy=Ip/2, где Iр= πd4/32. I=πd4/64.
11)общий метод опр главн центр осей и мом инерц сложн сеч.радиусы и эллипс инерцииЦентробежный момент инерции сечения — сумма произведений элементарных площадок на их расстояния от двух взаимно перпендикулярных осей. .
Центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с осями симметрии, равен нулю.
Осевые и полярные моменты инерции всегда положительны, центробежные моменты инерции могут быть положительными, отрицательными или равными нулю.
Момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.
Радиус инерции сечения — геометрическая характеристика сечения, связывающая момент инерции фигуры J с ее площадью F следующими формулами:
![]()
![]()
Отсюда, формула радиуса инерции:


Эллипс инерции в сопротивлении материалов, графическое изображение, используемое для вычисления осевых и центробежных моментов инерции плоской фигуры (например, поперечного сечения стержня) относительно осей, проходящих через её центр тяжести. При построении Эллипс инерции его полуоси, численно равные главным радиусам инерции фигуры, совмещаются с её главными центральными осями.
12) иследов напр сост в точке упр телаНапряженное состояние в точке тела — совокупность напряжений во мн-ве площадок, проходящих через заданную точку. Исследование напряженного состояния необходимо для расчета на прочность в сложном случае напряжения. Моделью служит куб, параллелепипед. σij: i — перпендикулярная ось, j — вдоль. Из условия равновесия элементарного куба τyx=τxy.F=τ·S=τxy·(dz·dy)·dx; τyx=dx·dz·dy·τxy. => τyx=τxy.
Напряженное состояние элементарного куба описывается 9 компонентами (3 нормальных, 6 касательных). Учитывая закон парности касат.напряжений (τyx=τxy), напряженное состояние описывается 6 компанентами.
Понятие о главных напряжениях. Через заданную точку всегда можно провести только 3 взаимноперпендик. площадки, в которых τ=0. Это главные площадки, а нормальные напряжения — главные напряжения. Взаимные соотношения между главными напряжениями: σ1≥σ2≥σ3.
Сущ. 3 вида напряженного состояния тела:
1. действует только одно главное напряжение σ1 — одноосное напряженное состояние (растяжение).
2. действуют σ1, σ2 — плоское напряженное состояние (двуосное).
3. объемное напряженное состояние (трехосное).
13) потенц энергия и Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.
В словесной форме закон звучит следующим образом:Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформацииДля тонкого растяжимого стержня закон Гука имеет вид:
![]()
Здесь F сила натяжения стержня, Δl — его удлинение(сжатие), а k называется коэффициентом упругости (или жёсткостью). Минус в уравнении указывает на то, что сила натяжения всегда направлена в сторону, противоположную деформации.
Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как
![]() Величина
E
называется модулем Юнга и зависит только
от свойств тела.Если ввести относительное
удлинение
Величина
E
называется модулем Юнга и зависит только
от свойств тела.Если ввести относительное
удлинение
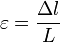 и
нормальное напряжение в поперечном
сечении
и
нормальное напряжение в поперечном
сечении
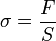 то
закон Гука запишется как
то
закон Гука запишется как
![]() В
такой форме он справедлив для любых
малых объёмов вещества.
В
такой форме он справедлив для любых
малых объёмов вещества.
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.Потенц. энергия элемента может рассм-ся как сумма независ.работ каж.из 6 силовых факторов, т.е. как сумма энергий кручения, изгиба, растяжения и сдвига: dU=dU(Mk)+dU(Mx)+dU(My)+dU(N)+dU(Qx)+dU(Qy). Это выполняется при опред. условиях, что точка приведения сил совп. с центром тяжести сечения, оси X, Y д.б. главными. dU(Mk)=Mk2dz/(2GIk), dU(Mx)= Mx2dz/(2EIx), dU(My)= My2dz/(2EIy), dU(N)=N2dz/(2EF), dU(Qx)=kxQx2dz/(2GF), dU(Qy)= kyQy2dz/(2GF), где kx, ky — безразмер. вел-ны, завис. от геометрич. формы сечения (для прямоуг. сечения k=kx=ky=1,2; сплошного круглого сечения k=10/9, тонкостен. кругового профиля k=2 и т.д.). Чтобы получить потенц. энергию всего стержня, надо проинтегрировать выражение dU по длине l.
14)теории прочности Первая теория.В основу теории наибольших нормальных напряжений (Галилей, 1638 г) положена гипотеза о преимущественном влиянии наибольших по абсолютной величине нормальных напряжений.Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее из главных напряжений достигает величины, соответствующей пределу прочности при простом растяжении.
В этом случае условие прочности должно иметь вид:
![]() - при растяжении,
- при растяжении,
(9.18)
![]() - при сжатии.
- при сжатии.
(9.19)
Данная гипотеза удовлетворительно согласуется с результатами испытания деталей из хрупких материалов, таких как камень, кирпич, чугун. Для расчета деталей из пластичных материалов данная гипотеза непригодна.
Вторая теорияВ основу теории наибольших линейных деформаций (Мариотт, 1682 г.) положена гипотеза о преимущественном влиянии наибольших по абсолютной величине линейных деформаций.
Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее из относительных удлинений достигает опасной величины, соответствующей пределу прочности при простом растяжении.
Максимальные относительные деформации в соответствии с обобщенным законом Гука (3.36)
![]() -
при растяжении,
-
при растяжении,
(9.20)
![]() - при сжатии
- при сжатии
(9.21)
При простом
растяжении
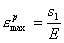 (9.22)
(9.22)
Предельное значение
относительной деформации при растяжении
![]()
(9.23)
На основании
сформулированной гипотезы, имеем
![]()
или с учетом (9.20),
(9.23)
![]() (9.24)
(9.24)
Сравнивая с условием
наступления предельного состояния
(9.2), получим эквивалентное напряжение
по II
теории прочности: ![]() (9.25)
(9.25)
Условие прочности в соответствии с (9.1) имеет следующий вид:
![]() - при
растяжении, (9.26)
- при
растяжении, (9.26)
![]() - при
сжатии. (9.27)
- при
сжатии. (9.27)
Из (9.26), (9.27) вытекает, что простое растяжение более опасно нежели сложное. Опыты этого не подтверждают. В связи с этим данная теория для расчета деталей не используется
15)Чистый сдвиг – частный случай плоского напряженного состояния, при котором по граням прямоугольного элемента действуют только касательные напряжения. Определим величину и направления главных напряжений при чистом сдвиге:
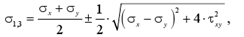
![]() можем записать:
можем записать:
![]()
Направление главных
площадок определяется углом альфа,
который найдём по форумле: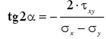
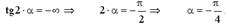
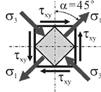 Как
видим, при чистом сдвиге главные
напряжения одинаковы по величине,
противоположны по знаку и направлены
под углом 45 к оси стержня.
Как
видим, при чистом сдвиге главные
напряжения одинаковы по величине,
противоположны по знаку и направлены
под углом 45 к оси стержня.


Тогда окончательно
запишем взаимосвязь между относительным
и абсолютным сдвигом элемента
![]()

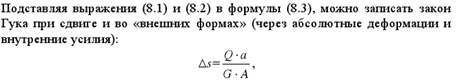

16.понятие
о кручении кругл стержней.осн гипотезы
и опр крут моментов.опр напр и
деф.Гипотезы:1.
до деформ остаются плоскими после
деформ.2.радиус сечения при деформации
не меняется3.растояние между сечениями
остаются не изменными .
Такой вид деформации, при котором в
поперечных сечениях возникает только
одни крутящие моменты — Мк.
Знак крутящего момента Мк
удобно определять по направлению
внешнего момента. Если при взгляде со
стороны сечения внешний момент направлен
против час.стр., то Мк>0
(встречается и обратное правило). При
кручении происходит поворот одного
сечения относительно другого на угол
закручивания
-.
При кручении круглого бруса (вала)
возникает напряженное состояние чистого
сдвига (нормальные напряжения отсутствуют),
возникают только касательные напряжения.
Угол закручивания
![]() ,
GJp
— жесткость
сечения при кручении.
,
GJp
— жесткость
сечения при кручении.
![]() — относительный
угол закручивания.
Потенциальная энергия при кручении:
— относительный
угол закручивания.
Потенциальная энергия при кручении:
![]() .
Условие прочности:
.
Условие прочности:
![]() ,
[]
=
,
[]
=![]() ,
для пластичного материала за пред
принимается предел текучести при сдвиге
т,
для хрупкого материала – в
– предел прочности, [n]
– коэффициент запаса прочности. Условие
жесткости при кручении: max[]
– допустимый угол закручивания.
,
для пластичного материала за пред
принимается предел текучести при сдвиге
т,
для хрупкого материала – в
– предел прочности, [n]
– коэффициент запаса прочности. Условие
жесткости при кручении: max[]
– допустимый угол закручивания.
18 Статически неопределимые задачи при кручении.
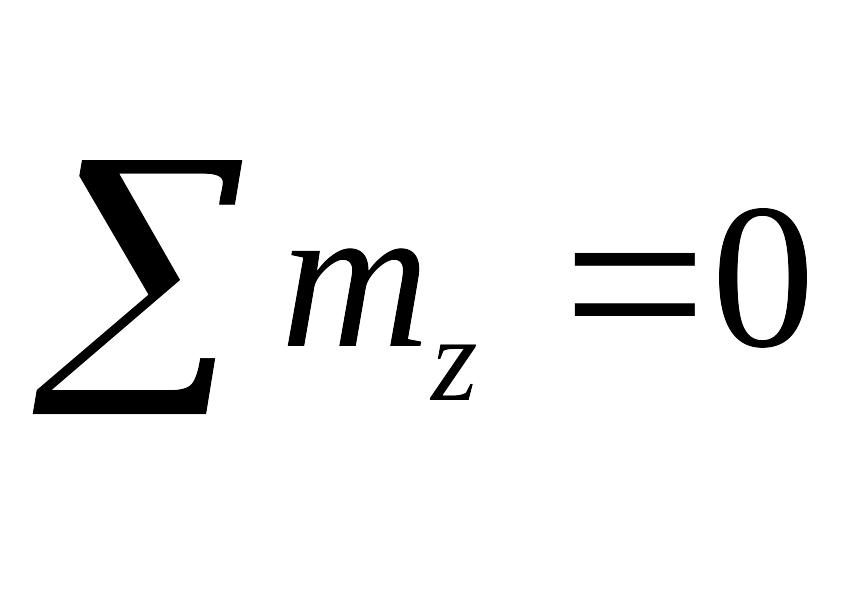 ;
;![]()
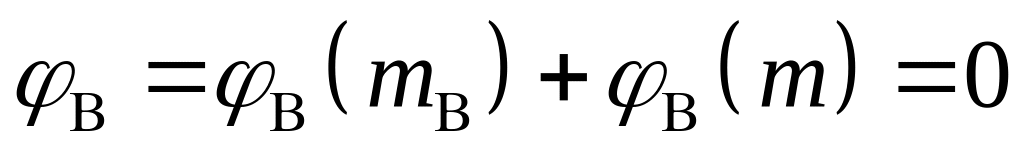 ;
;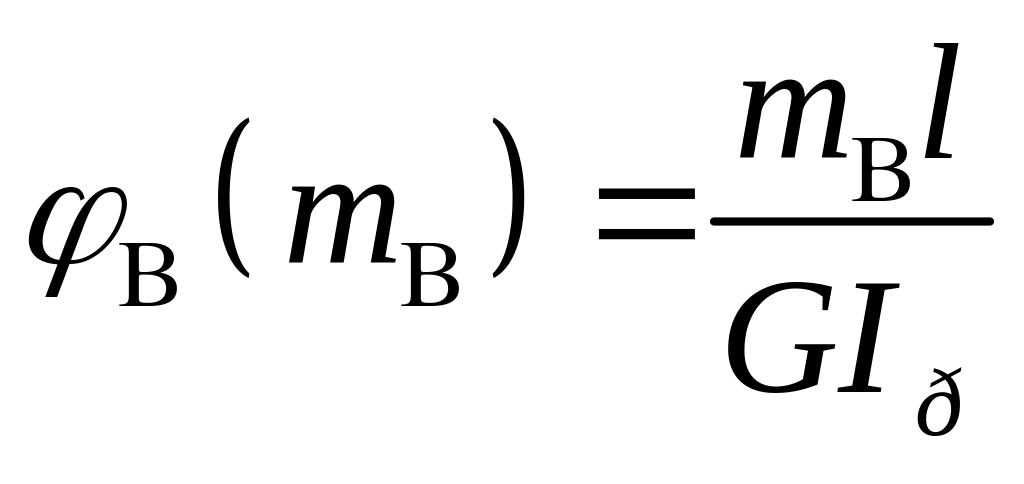
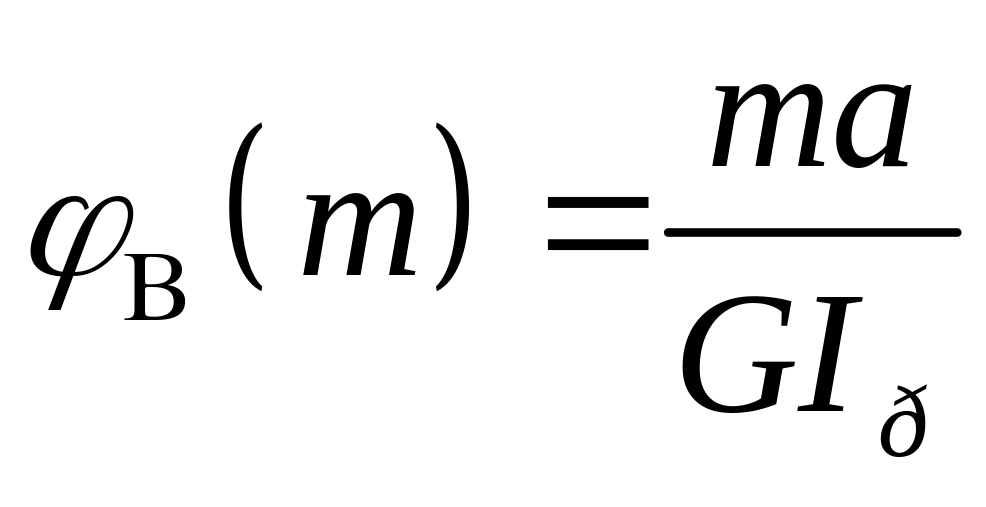
 ,
,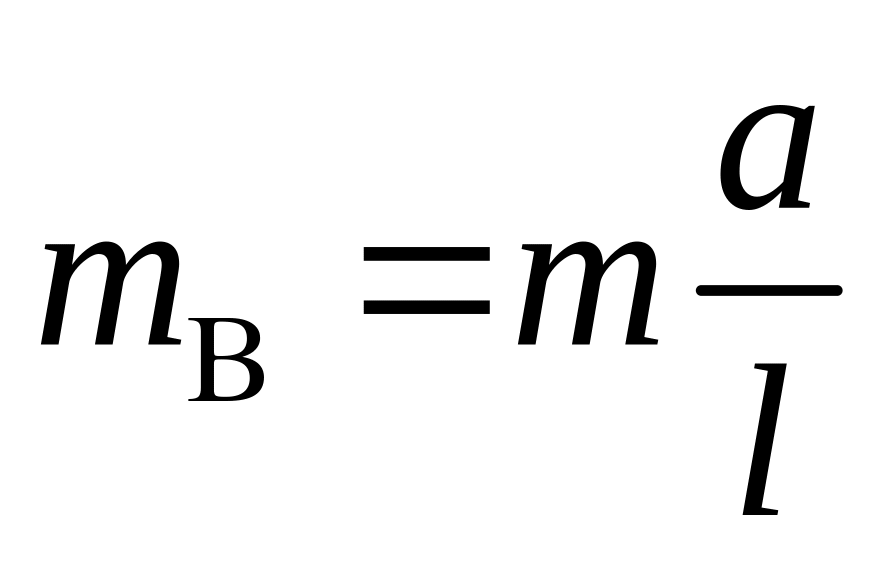
Потенциальная энергия при кручении:
Работа внешних сил А, затрачиваемая на кручение стержня, равна количеству потенциальной энергии U , накопленной в стержне:
![]() ;
;
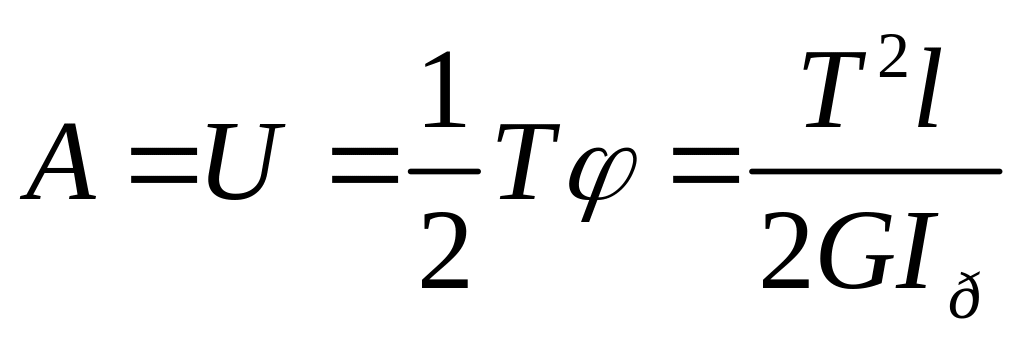
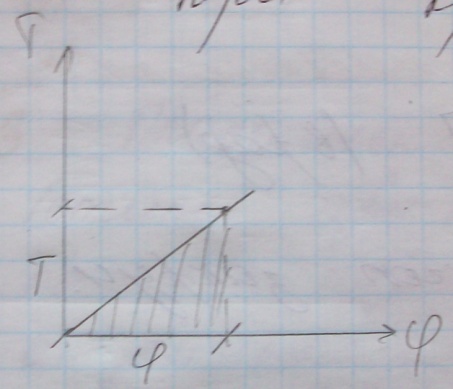
19.Расчёт винтовых цилиндрических пружин с малым шагом витка на прочность. Деформация винтовых цилиндрических пружин.
Ч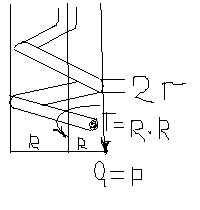 асть
1.Рассмотрим пружину растягиваюмую
силами P.
асть
1.Рассмотрим пружину растягиваюмую
силами P.
Р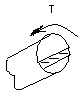 ассечем
ее и оставим нижнюю часть.
ассечем
ее и оставим нижнюю часть.
τ1= Q/A= P/πr2
τ2=T/Wp=2PR/πr3
Wp= πd3/16. τmax=τ1+τ2=P/πr2+2PR/πr3=(2PR/ πr3)(1+r/2R)
r/2R<<1, то можно пренебречь τmax=2PR/ πr3 τmax≤[τ]−условие прочности пружины
Часть 2.
А=![]() Pλ
U=T2∙L/2G∙Ip
Pλ
U=T2∙L/2G∙Ip
U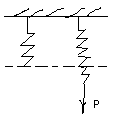 =P2R22πRn/2G
Ip=
P2R22πRn2/2Gπr4=2
P2R3n/Gr4
=P2R22πRn/2G
Ip=
P2R22πRn2/2Gπr4=2
P2R3n/Gr4
L=2πRn
Ip=πdφ/32=πr4/2
Pλ=2 P2R2πRn/Gr4 λ=4 P2R3n/Gr4
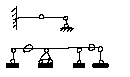
20. Типы балок и опор. Плоский поперечный изгиб. Построение эпюр поперечных сил (Q) и изгибающих моментов (М) (пример).Типы балок и опор.
Опоры:1)Шарнирно-подвижная опора
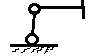 2)Шарнирно-неподвижная
опора
2)Шарнирно-неподвижная
опора
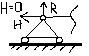 3)Заземление
или заделка
3)Заземление
или заделка
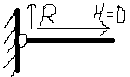 Типы
балок (стат.-определимых)
Типы
балок (стат.-определимых)
1) Консоль2)Однопролётная3)Одноконсольная, двухконсольная балка.
4) балки с промежуточным шарниром.
П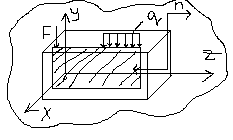 л.
поперечным изгибом
наз. такой вид изгиба, когда все силы
лежат в одной плоскости перпендикулярно
оси бруса, а плоскость их действия
совпадает с одной из главных осей
инерции.
л.
поперечным изгибом
наз. такой вид изгиба, когда все силы
лежат в одной плоскости перпендикулярно
оси бруса, а плоскость их действия
совпадает с одной из главных осей
инерции.
Qz=∑I
Mz=![]()
21.Построение эпюр в консольной балке.Диф зависимости.
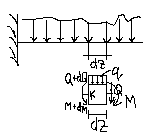
Дифференциальные зависимости между нагрузкой (q) поперечной силой (Q) и изгибающим моментом (М).
∑ z
= 0
z
= 0
-Q –q∙dz + Q + dQ =0
Q= dQ/dt = tgα
∑mk=0
-M-a∙dz – q∙dz+M+dM=-
Q=dM/dz = tgβ (теорема Журавского)
Q=dQ/dz=d2M/dz2
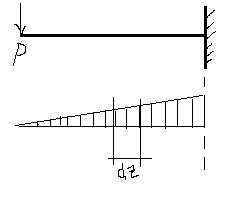
2 3. Определение касательных напряжений при изгибе (формула Журавского)
Эп. «М»
T – сдвигающая сила,∑z = 0;N2-N1-T = 0;N2=Aотс∫Ϭ2∙y∙dA= ((M+dM)S_x^отс)/Ix;
N1= Aотс∫ Ϭ1∙y∙dA = (M∙S_x^отс)/I_x
Будем считать, что кас-е напряжение по площади рассекается равномерно.
T=τ∙A = τ∙dzb; (dM∙S_x^отс)/I_x = τ∙dzb
dM/dz =Qy – теорема Журавского; τ = (d∙M∙S_x^отс)/(I_x∙b∙dz) = (Q∙S_x^отс)/(I_x∙b)
τ
= (Q∙S_x^отс)/(I_x∙dy)
- формула Журавского; Ix-момент
инерции,b-ширина
сечения в месте где определяем
τ.
В поперечном сечении: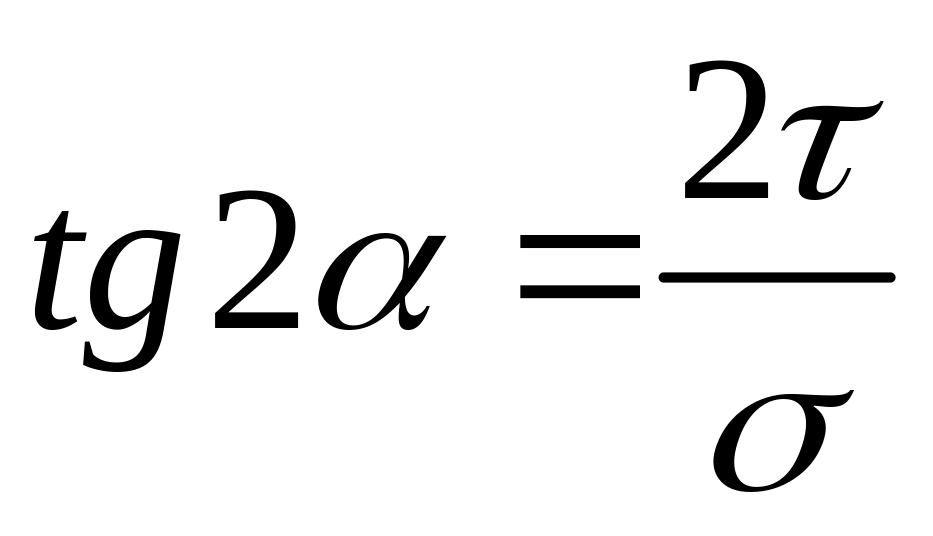
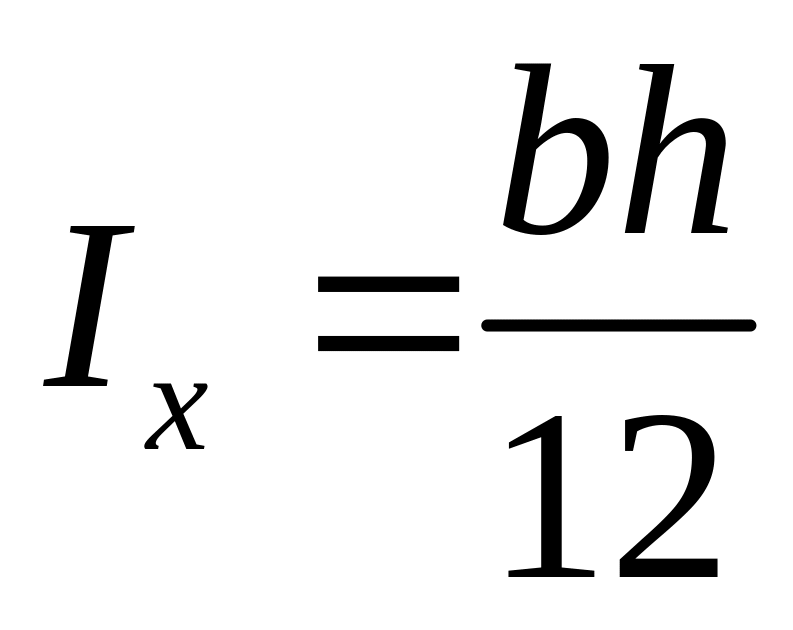 ,
,
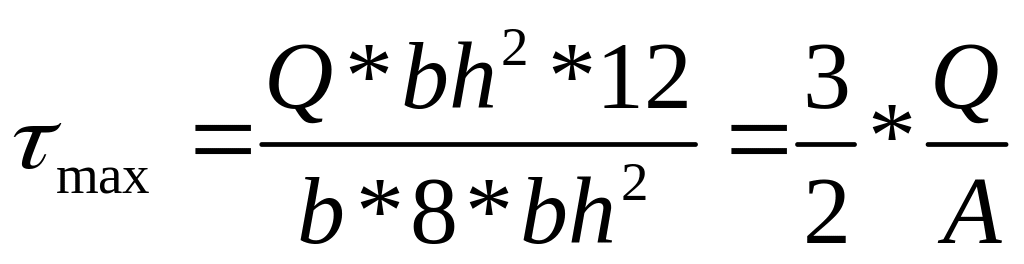
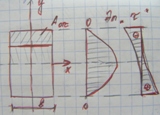
24. Главные напряжения при изгибе.
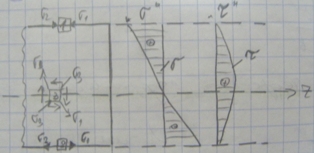 Q>0,M>0
Q>0,M>0
 ,
,
![]() ,
,
![]()
![]()
Экстремальное
касательное напряжение опр.по формуле: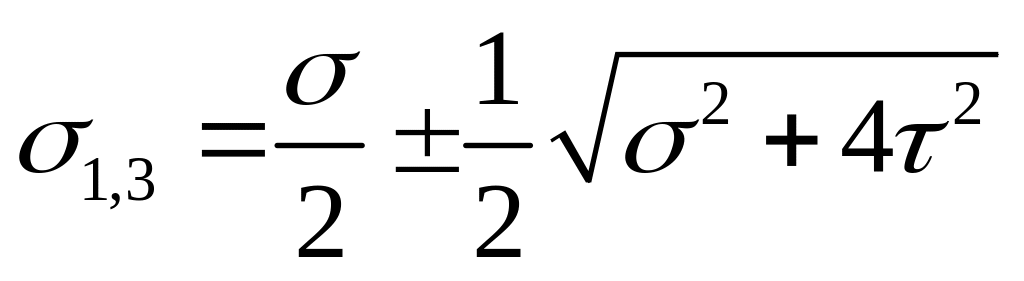 ,
две взаимно перпендикулярные наклонные
плоскости являются главными плоскостями
напряжений в данной точке балки,когда:
,
две взаимно перпендикулярные наклонные
плоскости являются главными плоскостями
напряжений в данной точке балки,когда: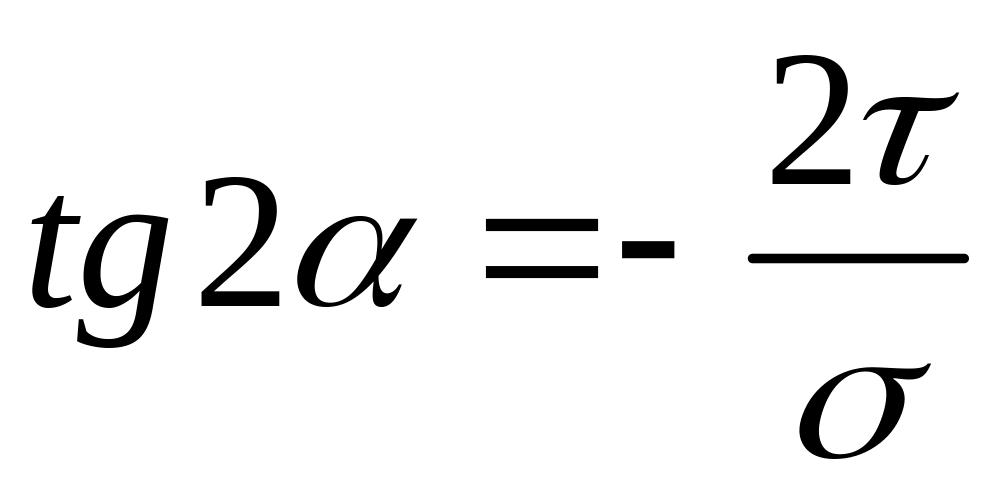
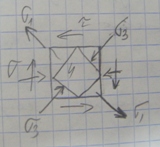
25.Подбор сечений и проверка прочности балок.
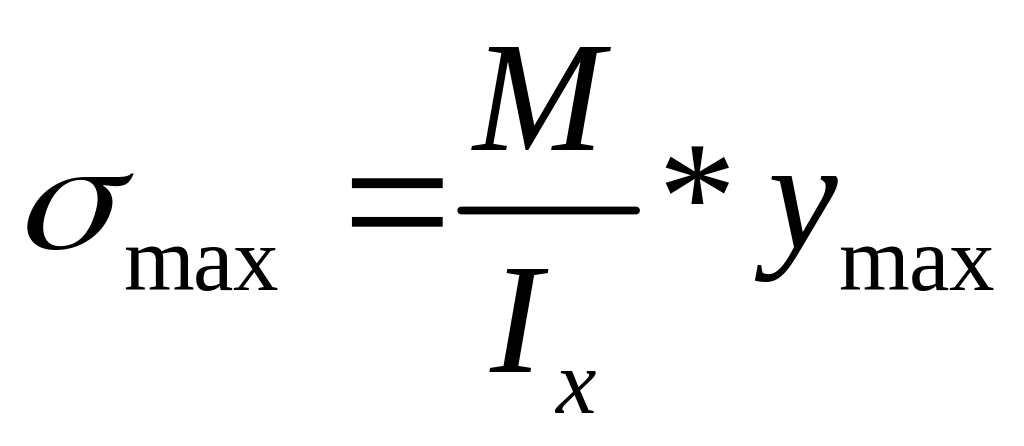 ;
;
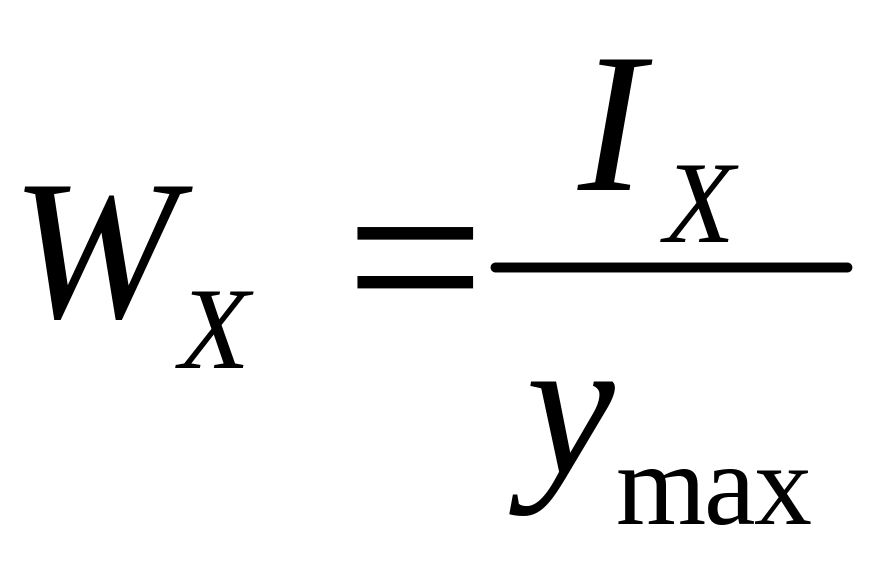 -осевой
момент сопротивления
-осевой
момент сопротивления
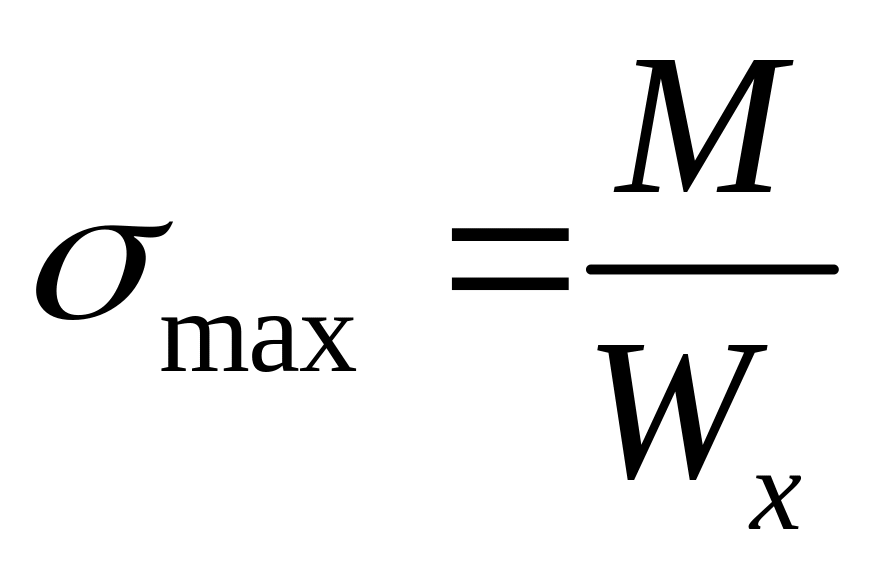 ;
;
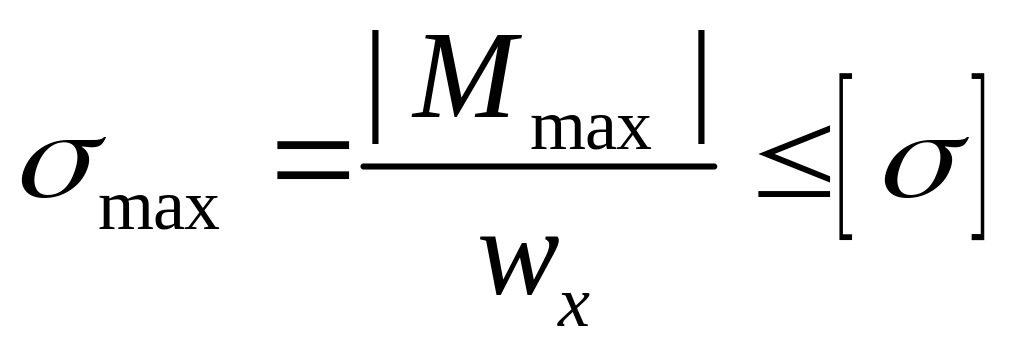 -условие
прочности при нормальном напряжении
-условие
прочности при нормальном напряжении
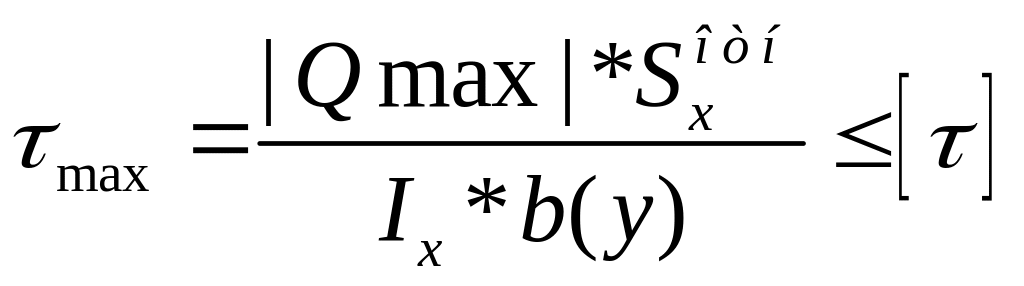
Балки
из пластичного материала проверяются
на прочность по третьей гипотезе:![]()
![]() подбор
сечений производится из условий прочности
по нормальным напряжениям.Если в одном
и том же поперечном сечении балки
одновременно действуют максимальный
изгибающий момент и и максимальная
поперечная сила или величины Q
и М, близкие к максимальным, то в этом
сечении производится проверка прочности
балки по главным напряжениям.Прочность
по главным напряж. Проверяется только
для балок,поперечное сечение которых
имеет тонкую стенку,резко уширяющуюся
вблизи крайних волокон.
подбор
сечений производится из условий прочности
по нормальным напряжениям.Если в одном
и том же поперечном сечении балки
одновременно действуют максимальный
изгибающий момент и и максимальная
поперечная сила или величины Q
и М, близкие к максимальным, то в этом
сечении производится проверка прочности
балки по главным напряжениям.Прочность
по главным напряж. Проверяется только
для балок,поперечное сечение которых
имеет тонкую стенку,резко уширяющуюся
вблизи крайних волокон.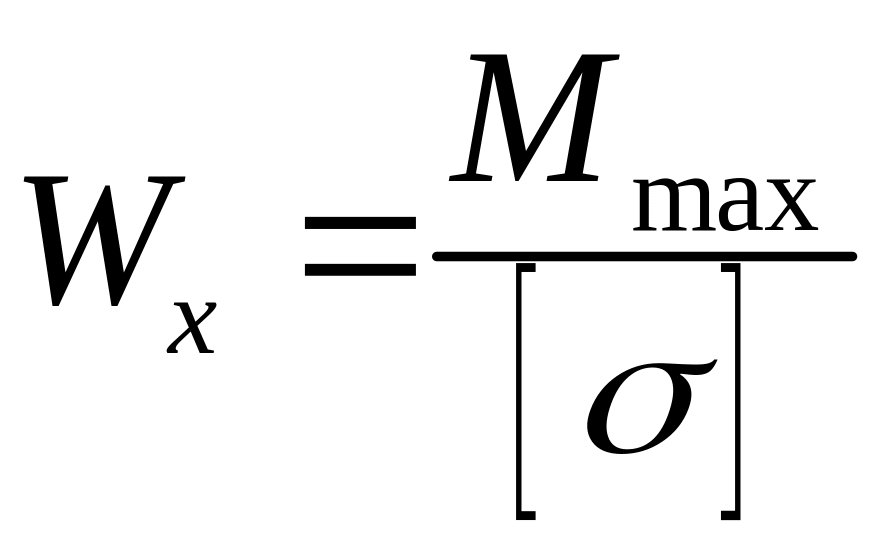 -в
точках ,где имеет место резкое расширение
ширины.
-в
точках ,где имеет место резкое расширение
ширины.
