49 Выведите формулу Байеса. Приведите примеры.

Следствием правила умножения, и формулы полной вероятности является теорема гипотез или формула Байеса.

По условиям опыта известно, что

гипотезы   несовместны, образуют полную группу событий:  Ø при   и  .Вероятности гипотез до опыта (так называемые «априорные вероятности») известны и равны

; 

Предположим, что опыт произведен и в результате появилось событие A. Спрашивается, как нужно пересмотреть вероятность гипотез с учетом этого факта, или, другими словами, какова вероятность того, что наступлению события A предшествовала гипотеза   (послеопытные вероятности называются апостериорными):

ероятность наступления события A совместно с гипотезой H_k определяется с использованием теоремы умножения вероятностей:

P(AÇH_k)=P(H_k)×P(A/H_k)=P(A)×P(H_k/A). (3.6)

Таким образом, можно записать:

P (H_k/A) =P (H_k) ×P (A/H_k)/P (A). (3.7)

С использованием формулы полной вероятности

Формула (3.8) называется формулой Байеса. Она позволяет пересчитывать вероятности гипотез в свете новой информации, состоящей в том, что опыт дал результат А

52. Докажите теорему умножения математических ожиданий. Что понимается при этом под произведением случайных величин х и у?

Теорема. Математическое ожидание произведения двух независимых случайных величин и равно произведению их математических ожиданий:

.

Доказательство. Пусть случайная величина принимает значения ( , ) ( ) и ( , ) ( ) – законы распределения случайных величин и . Так как и – независимы, то полный набор значений случайной величины состоит из всех произведений ( , ), причем вероятности этих значений по теореме умножения для независимых событий равны .

Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин.

58. Что такое «правило 3σ» для нормального распределения?

Случайная ошибка, возникающая при измерении некоторой величины, может теоретически принимать любые значения. Она является непрерывной случайной величиной, подчинённой определённому закону распределения вероятности.

Наиболее часто встречающиеся на практике ошибки распределены по нормальному закону: При этом

С какой вероятностью измеренная величина будет отклоняться от своего точного значения не больше, чем на σ? Очевидно с той же самой, с которой ошибка измерения будет находиться в промежутке [–σ; σ]. Если случайная ошибка распределена по нормальному закону, то для ответа на этот вопрос необходимо вычислить интеграл 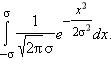Расчёты показывают, что в 68,27 % отклонения случайной величины, распределённой по нормальному закону, не превышают σ, в 95,45 % – 2σ. Наконец, вероятность того, что случайная величина, распределённая нормально, отклоняется от математического ожидания больше, чем на 3σ, пренебрежимо мала и составляет 0,27 % – правило трёх сигм.

1

Рисунок 4.3.8.1. Правило трёх сигм

73) Чем объясняется понятие плотность вероятности справедливо равенство ,По теореме о среднем интеграл, стоящий в правой части, равен , где – некоторая точка из интервала . Отсюда

. Представим себе, что интервал стягивается к некоторой точке , причем в этой точке функция f(x) непрерывна. Тогда будет стремиться к числу , и мы получим:

.Отношение, стоящее под знаком предела, есть своего рода "вероятность на единицу длины" интервала . Предел этого отношения естественно рассматривать как плотность вероятности в самой точке . Мы видим, таким образом, что во всякой точке , где f(x) непрерывна, число f(x) совпадает с естественно понимаемой плотностью вероятности в точке . Отсюда и название для функции f(x) – "плотность вероятности".

74) (3;2)= (перестановки с повторениями)

77)Из партии содержащей 17 стандартных и 4 бракованных отбирают на удачу 6 изделий пусть х число бракованных изделий в выборке найдите мх и постарайтесь объяснить результат. Смысл числа заключается в том, что около числа колеблется среднее арифметическое значений, принимаемых величиной X в больших сериях опытов. Результат означает, что при большом числе опытов всреднем будет вытащена 1 бракованная деталь.

79.Какие события А и В называются не совместными? что такое правило сложения вероятностей События А и В несовместные, если они не могут наступить вместе в одном опыте. Теорема слож. вер-тей. Для любых соб. A и B выполняется формула P(A+B)=P(A)+P(B)-P(AB)Док-во: Обозначим через n= - общее число исходов, ns- число исходов, благоприятных для соб. S.Тогда формулу = + – можно переписать след. образом nA+B=nA+nB-nAB(*).

Разделив почленно формулу (*) на n, получим формулу P(A+B)=P(A)+P(B)-P(AB)

Правило сложения вер-тей. Если соб. A и B несовместны, то P(A+B)=P(A)+P(B).Док-во:Т.е. соб. A и B несовместны, то P(AB)=0, поэтому из формулы P(A+B)=P(A)+P(B)-P(AB), получим P(A+B)=P(A)+P(B).

84) Пусть А и В случайные события по отношению к какому либо опыту причем P(B) неравно 0. число Р_B(А)=Р(АВ)/Р(В) называют вероятностью события А при условии что событие В уже наступило или просто условной вероятностью А. Наличие условной вероятности (Р_B(А)≠Р(А)) между событиями определяет их взаимосвязь.Статистическая интерпретация: Рассмотрим некий эксперимент и 2 соб. А и В. Повторим опыт к раз. Пусть - число опытов, в которых произойдет событие А при условии что В тоже произойдет.

1) Р_B(А)>Р(А) бросаем кость, В- выпало четное, А-выпала двойка. Р(А)=1/6 Р_B(А)=1/3

2) Р_B(А)<Р(А) в коробке лежит 3 белых и 3 черных шара вытащили 1 шар, А – вытащить черный шар, В- из коробки предварительно вынули шар оказавшийся черным.

Р(А)=1/2 Р_B(А)=2/5

Если выполняется равенство Р_B(А)=Р(А) то события А и В независимы. Пример: Пусть, например, рассматриваются события:

А — извлечение наудачу из колоды карты пиковой масти; В — извлечение наудачу из колоды туза. Необходимо выяснить, являются ли события А и В зависимыми. На первый взгляд, можно предполагать зависимость событий А и В в силу пересечения случаев, им благоприятствующих: среди карт пиковой масти есть туз, а среди тузов — карта пиковой масти. Убедимся, однако, в том, что события А и В независимы. Р(В) = 4/36 = 1/9 (в колоде 4 туза из 36 карт),

РА(В) = 1/9 (в колоде 1 туз из 9 карт пиковой масти).

Итак, РА(в) = Р(в), т.е. события Аи В независимы.

87) выведите формулу дисперсии суммы случайных велечин х и у как определяется и что характеризует ковариация Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин.

D(X+Y)=M - =M( +2XY+ ) - .

Обозначая М(Х)= , M(Y)= и учитывая, что для независимых случайных величин M(XY)=M(X)M(Y), получим

D(X+Y)=М +2 +М - - 2 - =[ М - ]+[ М - ]= D(X)+D(Y).

Ковариацией COV(X,Y) случайных величин X,Y называется математическое ожидание произведения отклонений X и Y.

Сov(X,Y)=M[(X-M(X)][Y-M(Y)] или М( ) = Cov(X,Y). где обозначает, как и раньше, отклонение величины X

На всякий случай доказательство: Пусть Х и У – две случайные величины. Положим, Z=X+Y По теореме сложения математических ожиданий будем иметь: М(Z)=M(X)+M(Y). Вычитая это равенство из предыдущего, получим: , где обозначает, как и раньше, отклонение величины Х. Отсюда = Найдем дисперсию Х+У. Имеем D(X+Y)=D(X)+D(Y)+2M( ), где М( ) = Cov(X,Y).

Формула принимает вид: D(X+Y)=D(X)+D(Y)=2Cov(X,Y)

Ковариация или корреляционный момент, как свидетельствует его название (от латинского слова correlatio – соответствие, взаимосвязь), играет определенную роль при оценке зависимости X и Y. Основное свойство ковариации выражается следующим предложением.

Если величины X и Y независимы, то их ковариация равна нулю.

Действительно, пусть X и Y независимы. Тогда, очевидно, величины и будут тоже независимы. Отсюда вытекает, что математическое ожидание произведения будет: .Из доказанного предложения следует: если Cov(X, Y) ¹ 0, то величины X и Y не могут быть независимыми. Таким образом, неравенство нулю ковариации определенно свидетельствует о наличии связи между величинами X и Y. Ковариация обладает следующими свойствами: 1. Cov(X, Y) = M(XY) − M(X)M(Y). 2. Cov(X, X) = D(X). 3. D(X+Y) = D(X) + D(Y) + 2Cov(X, Y). 4. Если X и Y независимы, то Cov(X, Y) = 0. 5. Cov(X, Y) = Cov(Y, X). 6. Cov(aX , Y) = Cov(X, aY) = aCov(X, Y). 7. Cov(X +Y, Z) = Cov(X, Z) + Cov(Y, Z). 8. Cov(X, Y + Z) = Cov(X, Y) + Cov(X, Z).

89 что такое правило умножения вероятностей а для независымых событий а и в . для любых а и в Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:

.

Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Решение. Обозначим события: А – вынули белый шар из первого ящика, ;

- вынули черный шар из первого ящика, ;

В – белый шар из второго ящика, ;

- черный шар из второго ящика, .

Нам нужно, чтобы произошло одно из событий или . По теореме об умножении вероятностей , . Тогда искомая вероятность по теореме сложения будет .

Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.

Решение.

Пусть А – попадание первого стрелка, ;

В – попадание второго стрелка, .

Тогда - промах первого, ;

- промах второго, .

Найдем нужные вероятности.

а) АВ – двойное попадание,

б) – двойной промах, .

в) А+В – хотя бы одно попадание,

.

г) – одно попадание,

.

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

Решение.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1.

2. .

3.

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

Если события имеют одинаковую вероятность , то формула принимает простой вид:

.

Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события (попадание первого орудия), (попадание второго орудия) и (попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям , и (т. е. вероятности промахов), соответственно равны:

, ,

Искомая вероятность .

Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События "машина работает" и "машина не работает" (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице:

Отсюда вероятность того, что машина в данный момент не работает, равна

Искомая вероятность

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Обозначим через А событие "при n выстрелах стрелок попадает в цель хотя бы один раз". События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула .

Приняв во внимание, что, по условию, (следовательно, ), получим

Прологарифмируем это неравенство по основанию 10:

Итак, , т.е. стрелок должен произвести не менее 5 выстрелов.