8. Докажите теорему сложения математических ожиданий. Что понимается при этом под суммой случайных величин?

Докажем, что для любых двух случайных величин х и у: М(х+у)=М(х)+М(у), т. е. математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий. Доказательство. а) Пусть (х,у) - система прерывных случайных величин. Применим к сумме случайных величин общую формулу для математического ожидания функции двух аргументов:

.

Ho  представляет собой не что иное, как полную вероятность того, что величина  примет значение :

;

следовательно,

.

Аналогично докажем, что

,

и теорема доказана.

9 Что называется функцией распределения случайной величины? Какой вид имеет

функция распределения дискретной случайной величины? Каждая случайная величина полностью определяется своей функцией распределения.

Если  .- случайная величина, то функция F(x) = F_ (x) = P( < x) называется функцией распределения случайной величины  . Здесь P( < x) - вероятность того, что случайная величина  принимает значение, меньшее x.

Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют простораспределением.

Функция распределения любой случайной величины обладает следующими свойствами:

• F(x) определена на всей числовой прямой R;

• F(x) не убывает, т.е. если x₁ x₂, то F(x₁)  F(x₂);

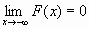• F(- )=0, F(+ )=1, т.е.   и  ;

• F(x) непрерывна справа, т.е. 

Функция распределения дискретной случайной величины

Если  - дискретная случайная величина, принимающая значения x₁ < x₂ < … < x_i < … с вероятностями p₁ < p₂ < … < p_i < …, то таблица вида

x1	x2	…	xi	…
p1	p2	…	pi	…

называется распределением дискретной случайной величины.

Соответственно график функции распределения имеет ступенчатый виД

10. Какой закон распределения называется нормальным? От скольких параметров зависит нормальное распределение? Как изменится график плотности нормального распределения при изменении параметров?

Если распределение вероятностей вызвано сложением большого количества случайных событий, каждое из которых мало влияет на результат, то это, скорее всего, распределение Пуассона. В аналогичном непрерывном случае получается распределение Гаусса, которое часто называют нормальным распределением. Плотность вероятности нормального распределения имеет вид:

В этой формуле a – математическое ожидание величины x, а σ – ее среднеквадратичное отклонение.

6

Рисунок 4.3.7.6. Плотность вероятности нормального распределения

Сумма двух нормальных распределений с параметрами и также является нормальным распределением с параметрами и

Нормальному распределению подчиняются случайные ошибки измерений.

11. Сколько различных "слов" можно составить из 5 букв "а" и 3 букв "в"? 1. Считаем все буквы разными а1 а2 а3 а4 а5 в1 в2 в3 = 8!=40320 2. Считаем буквы одинаковыми (повторения) а1 а2 а3 а4 а5 = 5!= 120, в1 в2 в3=3!=6 3. Ответ 40320/(120*6)=56 "слов" 13. Каков смысл параметра λ в пуассоновском законе распределения.

Распределение Пуассона имеет следующую плотность вероятности:

Доказательство. Величина p_k (λ) соответствует вероятности ровно k удачных исходов при условии, что среднее число удачных исходов составляет λ. Этим распределением проще пользоваться, чем биномиальным. Параметр λ (напомним, что он определяется пределом Np → λ) здесь равен числу, которое соответствует математическому ожиданию величины x: Мх= λ, Dх= λ. Закон Пуассона действует всякий раз, когда имеется много независимых испытаний N, а вероятность p каждого испытания так мала, что среднее число событий λ = pN с данным исходом невелико.

18 Какой закон распределения называется биномиальным? Почему?Одним из наиболее широко известных распределений является биномиальный закон распределения.

Считается, что случайная величина имеет биномиальный закон распределения, если выполняются следующие предположения или схема Бернулли:

- имеется n независимых испытаний;

- каждое испытание имеет только два исхода, обозначенных как "успех" и "неудача";

- вероятность "успеха" p и "неудачи" q = 1 – p являются постоянными от испытания к испытанию.

Что считать "успехом" и "неудачей" - зависит от поставленной задачи.

Пример. При анализе качества выпускаемой продукции обнаружение контролером среди n деталей бракованного считается "успехом" и годного изделия - "неудачей".

При биномиальном распределении испытания должны быть независимыми. Это требование выполняется для экспериментов, где независимость вытекает из самого эксперимента (подбрасывание монеты, подбрасывание игральной кости) или в экспериментах с возвращением.

Пример. Предположим, 5 % деталей в корзине - с браком. Вероятность вытаскивания бракованного изделия при первом вытаскивании p = 0.05.Если первая деталь возвращается в корзину, то вероятность вытащить бракованную деталь сохраняется и равна p = 0.05.. В этом случае испытания являются независимыми. Если бракованная деталь не возвращается в корзину, то вероятность вытаскивания бракованной детали изменяется. Испытания не являются независимыми.

Вероятность того, что при n испытаниях случайная величина Х примет значение m, равное числу "успехов", определяется по биномиальному закону распределения в виде

Формула (1.38) носит название формулы Бернулли.

Биномиальное распределение имеет два параметра: n и p.

Среднее μ=np.

Дисперсия σ² = npq.

Пример. Производится 4 независимых выстрела, вероятность попадания p = 0.25.. Определить закон распределения случайной величины Х, равной числу попаданий.

Решение. Случайная величина Х распределена по биномиальному закону, которая в данном случае принимает значения 1, 2, 3, 4. Вероятность того, что случайная величина Х примет значение i, где i = 1, 2, 3, 4, определяется по формуле (1.38) в виде

.

Закон распределения представляется следующей таблицей (рядом распределения):

X	0	1	2	3	4
p	0.316	0.421	0.211	0.047	0.004

22. Что такое схема Бернулли? Какими числами она задается?

Под схемой Бернулли понимают конечную серию n повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают p=P(Y), а непоявления (неудачи) его p(H)=q=1-p. Бернулли установил, что вероятность ровно m успехов в серии из n повторных независимых испытаний вычисляется по следующей формуле: То значение M0, при котором число Pn(m)является максимальным из множества {Pn(m)}, называется наивероятнейшим, и оно удовлетворяет условию np - q <=m0<= np+ p, (m0ЭZ)

Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из k событий с вероятностью Pi(i=1,2,…,k). Вероятность появления m1 раз первого события и m2- второго и mk-k -го находится по формуле