Последовательность вычислений при проверке принадлежности данных нормальному закону распределения

j		mj			(		yj
1	2	3	4	5	6	7	8	9	10	11	12

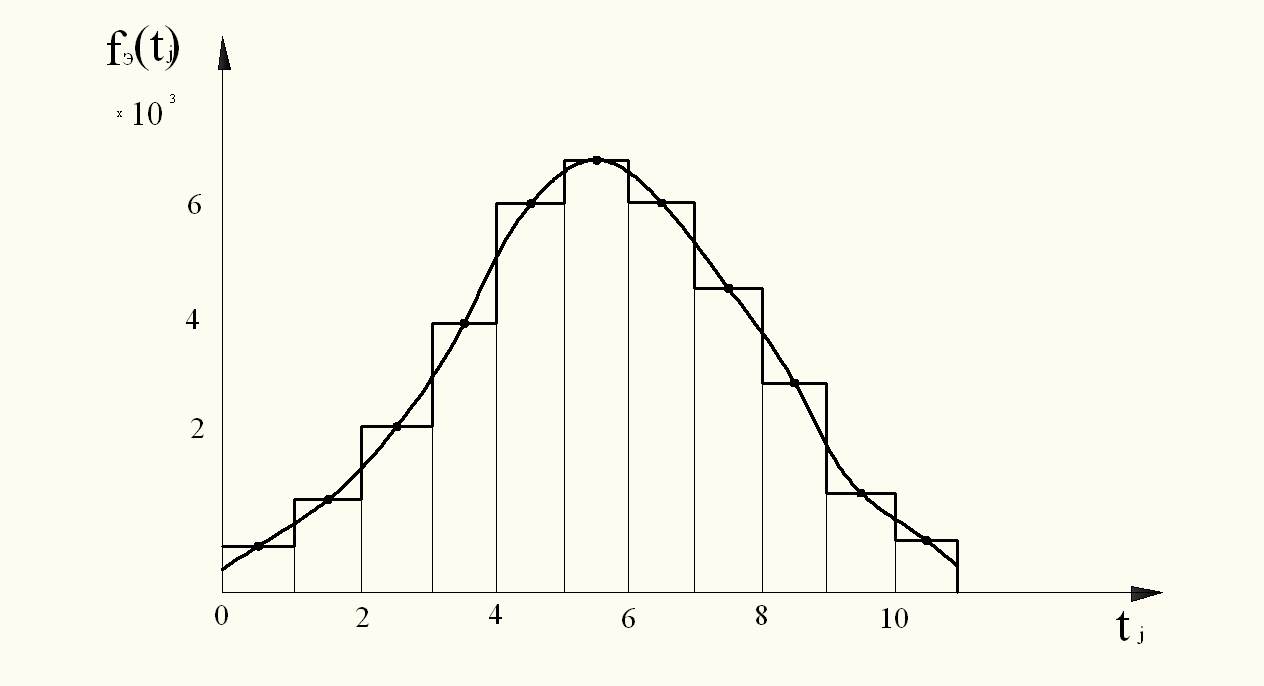
Рис. 1. График – гистограмма и полигон распределения

При вычислении значений эмпирической функции распределения по формуле (4) следует учесть, что в числителе берется сумма наб­людений, нарастающая от интервала к интервалу. Так, для первого интервала m₁ берется из первой строки графы 3 табл. 2, для вто­рого - сумма (m₁+m₂) из первой и второй строк графы 3 и т.д., а в последнем интервале (m₁+m₂+…m_n=N) значение эмпи­рической функции распределения будет равно единице.

Эмпирическая функция распределения рассматривается как некоторое приближение к соответствующей теоретической функции распределения. Степень приближения между этими функциями возрастает по мере увеличения числа наблюдений. Таким образом, имея некоторый эмпирический ряд распределения случайной величины, его описывают математи­ческой моделью - законом распределения.

3.2.3. Принятие гипотезы о виде закона распределения и определение оценки параметров закона распределения

Но внешнему виду гистограммы с учетом физических процессов, приводящих к отказу исследуемых элементов, выдвигают гипотезу о виде закона распределения. В нашем случае выдвинем гипотезу о том, что эмпирические данные о распределении наработок до отказа технологических систем соответствуют нормальному закону распределения.

Выполним промежуточные вычисления и полученные значения внесем в графу 4 табл. 2 и, воспользовавшись суммой этих значений, по формуле (5) вычислим оценку математического ожидания:

. (5)

Рассчитываем промежуточные значения для оценки среднего квадратического отклонения и заносим полученные результаты в графы 5...7 табл. 2.

По формуле (6) определяем оценку среднего квадратического отклонения:

. (6)

Вычисляем оценку коэффициента вариации:

. (7)

Судя по значению коэффициента вариации, делаем предварительное заключение о правомерности выдвинутой гипотезы о виде распределения. При нормальном законе распределения коэффициент вариации обычно не превышает 0,3...0,4.

4. Определение теоретических характеристик распределения

Предварительно рассчитываются центрированные и нормированные отклонения середин интервалов:

, (8)

где - значения середин интервалов (из графы 2 табл. .2);

- значение оценки математического ожидания; - значение оценки среднего квадратического отклонения.

Полученные значения вносятся в графу 8 табл. 2.

По выражению (9) определяются значения теоретической плотнос­ти распределения вероятностей и полученные значения заносятся в графу 10 табл. 2:

, (9)

где - значение оценки среднего квадратического отклонения;

. (10)

При аргументе, выраженном в этом случае в средних квадратических отклонениях, плотность распределения вероятности нормированного распределения табулирована и имеет вид (10).

Значения табулированной функции (10) находятся из табл. 3 приложения. Для определения табулированного значения функции знак нормированной переменной не имеет значения, т.к. . После того, как найдено табличное значение функции , это табличное значение в соответствии с формулой (9) делится на средние квадратическое отклонение и находится значение теорети­ческой плотности распределения вероятностей.

Вычисляют значение теоретической функции распределения, кото­рая в отличие от эмпирической функции , выражающей относи­тельную частоту события, определяет вероятность события.

Значения теоретической функции распределения определяют по одному из трех выражений (11), (14), (15):

, (11)

где

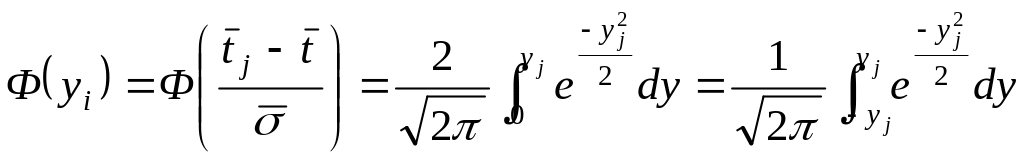. (12)

табулированный интеграл Лапласа, соответствует площади под кри­вой, заключенной между осью симметрии и ординатой, соответствую­щей значению t, и определяет вероятность того, что значение случайной величины находится в пределах от 0 до t.

Значение находят по табл. 4 приложения. При этом следует иметь в виду следующее правило знаков:

, (13)

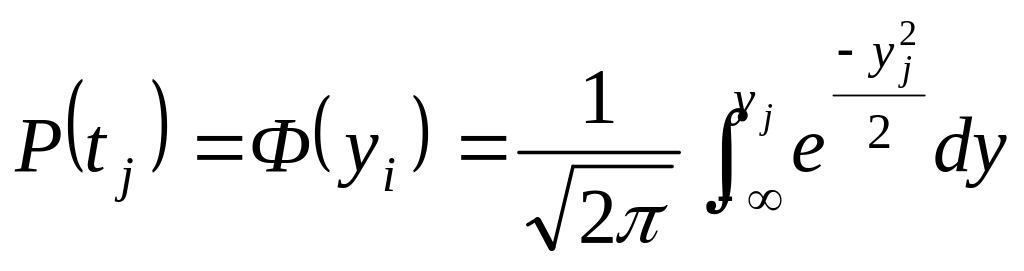, (14)

где

; .

Значения табличного интеграла Лапласа, равные значению нормаль­ной функции распределения , принимают в зависимости от значения центрированного и нормированного отклонения :

, (15)

где 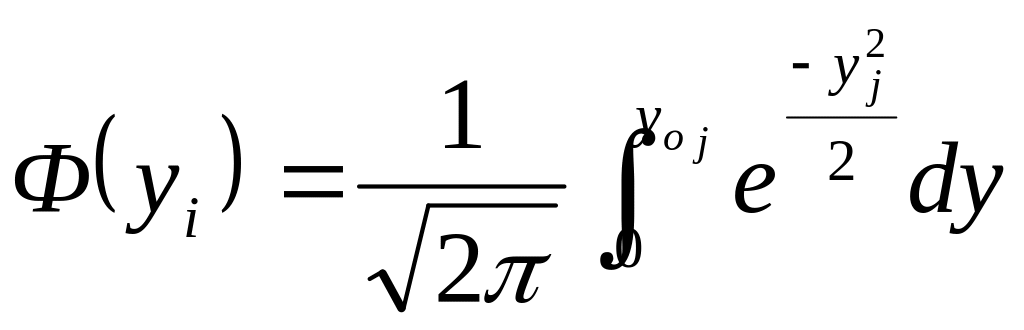– табулированный интеграл Лапласа.

При этом учитывается правило знаков (см. формулу 13).

Для удобства вычисления значений теоретической плотности рас­пределения и теоретической функции распределения (по формуле (11)) промежуточные вычисления могут быть представлены в виде табл. 3.

Таблица 3