
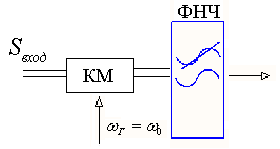
- •1. Многоканальные системы передачи: определение, структурная схема, основные понятия и классификация. Понятие о перекрестных помехах..
- •2) Требования к канальным сигналам:
- •2. Частотный спектр периодического сигнала, математический аппарат
- •3. Задача
- •4. Необходимые и достаточные условия для выбора канального сигнала в многоканальной системе передач
- •5. Вид спектра частотного спектра непериодического сигнала, математический аппарат
- •6. Задача
- •7) Плюсы и минусы систем с чрк:
- •8. По какому параметру сигнала определяется практическая ширина его частотного спектра..
- •9. Задача
- •1) Фильтры
- •2) Преобразователи частот.
- •11. Что такое помехоустойчивость сигнала и в каких единицах она измеряется
- •13. Амплитудная модуляция: определение, описание, частотный спектр, классификация.
- •Формирование обп (Однополосная боковая) сигнала
- •Детектирование
- •14. Пропускная способность сигнала.
- •16. Многоканальные системы с временным разделением каналов. (врк): определение, блочная схема, классификация и особенности этих систем.. Применение систем врк.
- •3. Системы с очень большим числом каналов
- •1. Низкая эффективность использования группового тракта
- •2. Необходима широкая полоса пропускания
- •17. Как определяется пропускная способность канала передачи.
- •19. Многоканальные системы передачи с разделением каналов по форме и уровню сигнала: определение, блочные схемы. Применимость этих схем.
- •23. Сформулируйте теорему отсчетов (Котельникова) и в чем ее значение.
- •25. Системы передачи дискретной информации: определение, классификация и общая функциональная схема системы. Основные функциональные узлы системы и их назначение.
- •26. Квантование
- •28. Кодеры и декодеры
- •29. Импульсно-кодовая модуляция (икм)
- •31. Многоканальная система с временным разделением каналов
- •32. Что означает понятие «канал передачи» и «линия связи»
- •34. Синхронизация и тп. Синхронно-адресные многоканальные системы
- •35. Что такое «операция модуляция»?
- •36. В канале с центральной частотой ω0 действует флуктационная (непрерывная) помеха с дисперсией . Определите мощность огибающей и квадратурных составляющих помехи?
- •37. Непрерывная тактовая синхронизация в системах с врк: определение, разновидности и особенности. Синхронизаторы на резонансном контуре: функциональная схема построения и особенности его применения.
- •38. Что такое “операция кодирования” и понятие “код”.
- •41. Что называется “системой передачи информации” и ее основные части?
- •43. Требование к кодовым сигналам передаваемых по линии связи в дискретных (цифровых) систем передачи. Типы линейных кодов. Регенераторы сигналов: их назначение и схемные решения.
- •44. В каких единицах измеряются скорости передачи сигнала и информации?
- •46. Искажение дискретных сигналов: виды, источники их происхождение.
- •47. Белый шум
- •50. Что называем непрерывно-дискретным и дискретным сигналами и изобразите их
- •Метод комбинационно-распределительный.
- •59. Что такое значащий момент времени (змв) сигнала?
- •62. «Посылка» и «команда» - в чем разница?
- •63. Телефонный канал имеет полосу пропускания 0,3-3,4 кгц. Вычислите его пропускную способность при отношении сигнал/шум на выходе 20 дб.
- •64. Непрерывная (флуктуационная) помеха: определение, описание, параметры и характеристики. Методы борьбы с непрерывной помехой.
- •65. Чем определяется свойство (возможности) корректирующего кода?
- •67 Помехоустойчивость передачи дискретной информации: определение, оценка и классификация. Оценка помехоустойчивости кодового сигнала и методы ее повышения.
- •Классификация помех.
- •68. Что такое “спектральная плотность” сигнала и в каких единицах она измеряется?
- •70. Помехоустойчивость элементарного двойного сигнала. Понятие простого двоичного канала и его оценка. Методы повышения помехоустойчивости приема элементарного двоичного канала..
- •Активная помехоустойчивость
- •Пассивная помехоустойчивость
- •Оценка элементарного сигнала
- •71. В чем разница между понятием “линия связи” и “линейный тракт передачи” и “канал связи”
- •73. Потенциальная помехоустойчивость
- •Критерий Байеса
- •74. «Энтропия» источника информации и единица ее измерения?
- •76. Потенциальная помехоустойчивость:определение. Оптимальный приемник двойных сигналов на согласованном фильтре, условия построения фильтра и особенности его применения.
- •79. Циклическая синхронизация в системах передачи с врк: назначение и организация.
- •Особенности цикличной синхронизации частот
- •80 Импульсная помеха и ее характеристики.
Детектирование
Демодуляция (или выделение из сложного сигнала сообщения), называется детектированием. Детектирование сводится к воздействию полученного амплитудно-модулированного сигнала на нелинейный элемент.
14. Пропускная способность сигнала.
Рассмотрим дискретный канал, через который передаются в единицу времени v символов из алфавита объемом m. При передачи каждого символа в среднем по каналу проходит следующее количество информации:
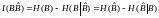 ,
(B с кракозяброй это B
со штрихом)
,
(B с кракозяброй это B
со штрихом)
где
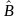 и В —случайные символы на выходе и входе
канала. Из четырех фигурирующих здесь
энтропий Н(В) — собственная информация
передаваемого символа — определяется
источником дискретного сигнала
(источником дискретного сигнала в
системе связи является совокупность
источника сообщения и кодера) и не
зависит от свойств канала. Остальные
три энтропии в общем случае зависят как
от источника сигнала, так и от канала.
Представим себе, что на вход канала
можно подавать символы от разных
источников, характеризуемых различными
распределениями вероятностей Р(В). Для
каждого такого источника количество
информации, переданной по каналу,
принимает свое значение. Максимальное
количество переданной информации,
взятое по всевозможным источникам
входного сигнала, характеризует сам
канал и называется пропускной способностью
канала. В расчете на один символ:
и В —случайные символы на выходе и входе
канала. Из четырех фигурирующих здесь
энтропий Н(В) — собственная информация
передаваемого символа — определяется
источником дискретного сигнала
(источником дискретного сигнала в
системе связи является совокупность
источника сообщения и кодера) и не
зависит от свойств канала. Остальные
три энтропии в общем случае зависят как
от источника сигнала, так и от канала.
Представим себе, что на вход канала
можно подавать символы от разных
источников, характеризуемых различными
распределениями вероятностей Р(В). Для
каждого такого источника количество
информации, переданной по каналу,
принимает свое значение. Максимальное
количество переданной информации,
взятое по всевозможным источникам
входного сигнала, характеризует сам
канал и называется пропускной способностью
канала. В расчете на один символ:
Ссимвол=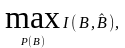 бит/символ,
бит/символ,
Можно определить пропускную способность С канала в расчете на единицу времени (секунду):
С=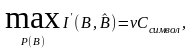 бит/с.
бит/с.
Последнее равенство следует из аддитивности энтропии. В дальнейшем, где это особо не оговорено, будем под пропускной способностью понимать пропускную способность в расчете на секунду.
Для двоичного симметричного канала (m=2) пропускная способность в двоичных единицах в секунду
С=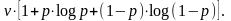
Пропускная способность непрерывного канала вычисляется аналогично. Пусть, например, канал имеет ограниченную полосу пропускания шириной F. Тогда сигналы U(t) и Z(t) на входе и выходе сигнала по теореме Котельникова определяются своими отсчетами, взятыми через интервал 1/(2F), и поэтому информация, проходящая по каналу за некоторое время Т, равна сумме количеств информации, переданных за каждый такой отсчет. Пропускная способность канала на один такой отсчет:
Сотсч=
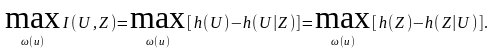
Здесь U и Z— случайные величины — сечения процессов U(t) и Z(t) на входе и выходе канала и максимум берется по всем допустимым входным сигналам, т.е. по всем распределениям u.
Пропускная способность С определяется как сумма значений Сотсч, взятая по всем отсчетам за секунду. При этом дифференциальные энтропии должны вычисляться с учетом вероятностных связей между отсчетами.
Переходя к пропускной способности С в расчете на секунду, заметим, что эта информация, переданная за несколько отсчетов, максимальна в том случае, когда отсчеты сигналов независимы. Этого можно достичь, если сигнал U(t) выбрать так, чтобы его спектральная плотность была равномерной в полосе F. Отсчеты, разделенные интервалами, кратными 1/(2F), взаимно некоррелированные, а для гауссовских величин некоррелируемость означает независимость.
Поэтому пропускная способность С (за секунду) можно найти, сложив пропускные способности для 2F независимых отсчетов: С=2FСотсч= . (*) – ф-ла Шеннона
Она реализуется , если U(t)—гауссовский процесс с равномерной спектральной плотностью в полосе частот F (квазибелый шум). Если бы мощность сигнала Рс не была ограничена, то пропускная способность была бы бесконечной. Пропускная способность равна нулю, если отношение сигнал/шум Рс/Рш в канаве равна нулю. С ростом этого отношения пропускная способность увеличивается неограниченно, однако медленно, вследствие логарифмической зависимости.
Соотношение (*) часто называют формулой Шеннона. Эта формула имеет важное значение в теории информации, т.к. определяет зависимость пропускной способности рассматриваемого непрерывного канала от таких его технических характеристик, как ширина полосы пропускания и отношения сигнал/шум. Формула Шеннона указывает на возможность обмена полосы пропускания на мощность сигнала и наоборот. Однако поскольку С зависит от F линейно, а от Рс/Рш — по логарифмическому закону, компенсировать возможное сокращение полосы пропускания увеличением мощности сигнала, как правило, нецелесообразно. Более эффективным является обратный обмен мощности сигнала на полосу пропускания.
Выразим
мощность шума в канале через его
одностороннюю спектральную плотность
N0. Имеем Рш=N0F;
поэтому С=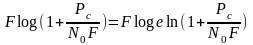 .
При С∞=
.
При С∞=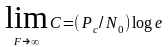 ,
бит/с.
,
бит/с.
