34. Понятие моделирования. Математическое моделирование.

Процесс решения задач на ПК можно разбить на следующие этапы:

1. Постановка задачи

2. Разработка математической модели задачи

3. Выбор численного метода решения задачи

4. Разработка алгоритма решения задачи

5. Разработка программы

6. Отладка программы

7. Проведение расчётов и анализ полученных результатов.

Одной из основных областей применения ЭВМ были и остаются научно-технические и экономические задачи. Решение такой задачи начинается с её математической формулировки, должны быть описаны известные и неизвестные соотношения между ними, а также должна быть чётко сформулирована цель, какие величины или функциональные зависимости ищутся, такое описание называется математической моделью задачи или математической моделью исследуемого процесса или объекта.

Прежде всего, должны быть выявлены величины, существенным образом характеризующие данный процесс или объект с позиции рассматриваемой задачи. Нужно определить, какие из них нам известны или могут быть определены экспериментально, а какие мы должны вычислить.

Необходимо также выяснить какие из этих величин находятся между собой в функциональной зависимости, а какие нет. Функциональные зависимости могут быть известны нам с самого начала, например, соотношения, вытекающие из законов физики, или они могут подлежать определению. Информация о том, какие величины независимые друг от друга также могут быть очень ценны.

Далее между известными и неизвестными функциями, их производными и интегралами также существуют определённые соотношения (их необходимо выявить). Всё это вместе с чётким описанием цели и расчётов и составляет математическую модель. Но практически никогда нельзя утверждать, что модель содержит все факторы, влияющие на рассматриваемый объект или процесс.

Искусство математического моделирования состоит в умелом отборе тех факторов, без учёта которых результат вычислений не может быть верным, и отбрасывания тех, влияние которых на результат не существенен.

35. Численные методы. Погрешность вычислений.

После того, как дана формулировка задачи и построена математическая модель, необходимо выбрать эффективный метод решения полученной математической задачи. Для решения математических задач используют три основные группы методов: графические, аналитические, численные.

Первые две группы методов позволяют получить решение в редких случаях. Основным инструментом для решения сложных математических задач в настоящее время являются численные методы, позволяющие свести решение задачи к выполнению конечного числа арифметических действий над числами. При этом результат получается в виде числовых значений. Обычно результат находится с некоторой погрешностью. Надо учитывать как сложность расчётных формул связанных с тем или иным методом, так и необходимую точность вычислений.

Есть четыре источника погрешности результата:

1) математическая модель,

2) исходные данные,

3) численный метод,

4) округление при вычислениях.

Погрешность математической модели связана с тем, что она охватывает важнейшие для данной задачи стороны явления, но не все. Исходные данные не точны, т.к. они являются результатами измерений или эксперимента. Погрешность исходных данных называется неустранимой погрешностью т.к. не зависит от исследователя. Погрешность метода связана с тем, что решение задачи сформулированной в терминах более сложных (производные, интегралы, диф. уравнения), сводится к вычислению в определённом порядке арифметических выражений. Например, интеграл заменяется суммой. Погрешность метода регулируема, т.е. она может быть уменьшена до любого разумного значения. Погрешность округления возникает из-за ограниченности разрядной сетки ЭВМ, т.е. число не может быть полностью записано в ячейку, приходится отбрасывать часть и в дробной части числа.

При решении больших задач выполняется миллиард операций и, казалось бы, что погрешность округления будет накапливаться в ходе вычислений. Однако при отдельных действиях, фактические погрешности числа могут иметь различные знаки и компенсировать друг друга. По результатам математической статистики, если нет систематических причин, то случайное накопление ошибок не слишком существенно.

36. Метод деления отрезка пополам для решения уравнений вида f(x)=0.

Пусть найден интервал [a, b], на концах которого функция f (x) имеет разные знаки, т.е. f(a)f(b)<0. Это означает, что на интервале [a, b] содержится несколько корней уравнения. Если интервал достаточно короткий, то корень один.

Интервал [a,b] делим на два : x = (a+b)/2 и получим 2 интервала [a,x] , [x,b]. Из двух интервалов выбираем тот, на концах которого функция имеет разные знаки, ибо этот интервал содержит корни. Выбранный интервал снова делим пополам, и из двух интервалов выбираем тот, на концах которого функция имеет разные знаки, либо этот интервал содержит корни и т.д. Если требуется найти корень с точностью ε, то деление продолжаем до тех пор, пока длина интервала не станет меньше ε, после этого любое число из этого интервала можно взять в качестве значения корня, вычисленного с точностью ε.

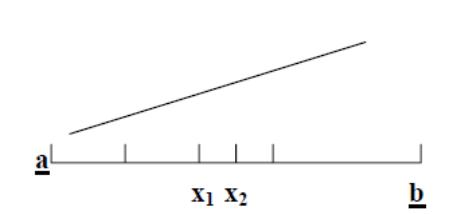
Алгоритм метода деления отрезка пополам.

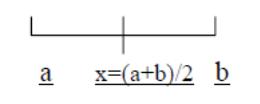Если f(a)f(х)<0 , то выбираем: иначе: Если (b-a)>ε , то: Если (b-a)<ε , то печатаем х. Конец.

Программа (исходные данные: f(x), a, b, ε):

DEF FNF(X) = f(x)

NPUT a, b, eps

2 x=(a+b)/2

IF FNF(a)*FNF(x)<0 THEN b=x ELSE a=x

IF (b-a)>ε THEN 2

PRINT x, FNF(x)

END.

Метод деления отрезка пополам - это простой и надёжный метод поиска простого корня, он сходится для любых непрерывных функций, в том числе и не дифференцируемых. Скорость сходимости не велика, для достижения точности ε необходимо выполнить:

n ≈ Log ₂ ( (b-a) / ε ) шагов,так как (b-a) / 2ⁿ ≈ ε.

37. Метод решения нелинейных уравнений f(x)=0. Метод Ньютона.

Если известно хорошее начальное приближение решения уравнения f(x) = 0, то эффективным методом повышения точности является метод Ньютона (метод касательных). Сформулируем достаточное условие сходимости метода.

Пусть функция f(x) определена и дважды дифференцируема на интервале от a до b, причём должно быть f(a)f(b)<0 , а производные f'(x) и f''(x) сохраняют знак на интервале от a до b. Тогда, исходя из начального приближения, Хо принадлежащие [a, b] и удовлетворяющих условию f(Хо) f"(Хо)>0 , можно построить последовательность: Х_к+1 = Х_к - (f(Х_к) / f'(Х_к)), К=0,1,2,3… , сходящуюся к единственному на интервале [a, b] корню уравнения f(x)=0. Метод Ньютона позволяет (допускает) простую геометрическую интерпретацию. Выберем начальное приближение: f(b)>0, f''(b)>0 (т.к. функция вогнута) и Xo=b. К точке кривой с абсциссой X0 проведём касательную.

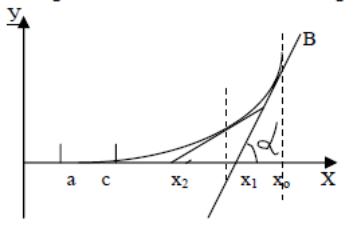
Точку пересечения касательной с осью абсцисс обозначим Х1,к точке с абсциссой X1 снова проведем касательную, точку ее пересечения сосью обозначим X2 и т.д. Таким образом будем продвигаться все ближе к точке С, пока расстояние до него не станет меньше ε. Получим условие остановки:

|Xk+1-C| < |Хк+1-Хк|< ε.

Выведем расчетные формулы метода. У нас ABC - прямоугольный треугольник. tgα = ВС/АС tgα = f'(x) BC = (Xo) AC = Xo-X

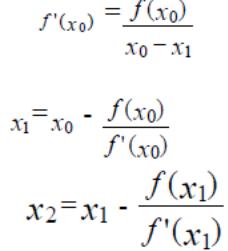Уравнение касательной:

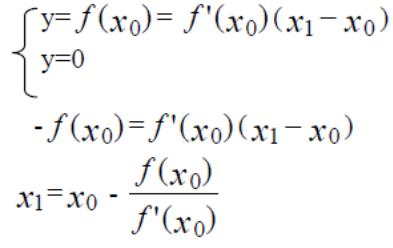
Программа (исходные данные: f(X),f'(X), Xo, ε)

DEF FNF (X)=f(x)

DEF FNP (X)=f'(x)

INPUT X, eps

2 Y=X - FNF(X)/FNP(X)

IF ABS(Y-X)<eps THEN 5

X=Y: GOTO 2

5 PRINT Y,FNF (Y) END.

38. Метод простой итерации для решения уравнений вида f(x)=0.

Метод состоит в замене исходного уравнения f(x)=0 эквивалентным уравнением х=φ(х) и построение последовательности: Хк+1 = φ(Хк),К=0,1,2,3…сходящейся к точному решению. Такую замену можно сделать многими способами:

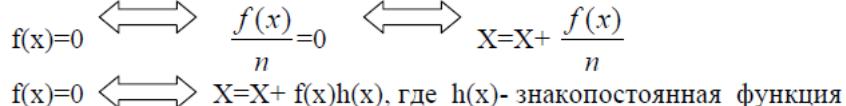n, h(x) выбирают удовлетворяющими условию сходимости метода.