4. Теоремы сложения и умножения вероятностей.

Теоремы сложения:

1) пусть А и B - два несовместных события, тогда вероятность их суммы равна сумме вероятностей слагаемых, т.е.

Р(А+B)=Р(А)+ Р(B)

2) пусть А и B - два совместных события, тогда вероятность их суммы равна сумме вероятностей слагаемых без вероятности произведения, т.е.

Р(А + B)=Р(А)+ Р(B)- Р(АB)

Теоремы умножения:

3) пусть А и B - два независимых события, тогда вероятность их произведения равна произведению вероятностей сомножителей, т.е.

Р(АB) = Р(А) Р(B)

4) пусть А и B - два зависимых события, тогда вероятность их произведения равна произведению вероятностей первого множителя на вероятность второго, вычисленную в предположении, что первое событие произошло (или вероятности второго множителя на вероятность первого, вычисленную в предположении, что второе событие произошло), т.е.

Р(АB)=Р(А) Р(B/А)=Р(B)Р(А/B)

5. Формула полной вероятности и формула Байеса.

Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., H_n, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H₁A, H₂A, ..., H_nA. Следовательно,

Применяя аксиому сложения вероятностей, имеем

Но (i=1, 2, ..., n), поэтому

Эта формула называется формулой полной вероятности. События H₁, H₂, ..., H_nназывают «гипотезами», при этом: P(H₁) + P(H₂) +…+ P(H_n) = 1

С формулой полной вероятности тесно связана формула Байеса. Если до опыта вероятности гипотез были P(H₁), P(H₂), ..., P(H_n), а в результате опыта появилось событие, то с учетом этого события "новые", т.е. условные вероятности гипотез вычисляются по формуле Байеса:

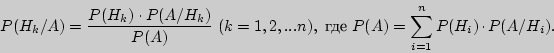
Д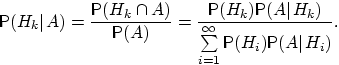 оказательство (по определению условной вероятности):

6.Дискретные случайные величины. Ряд распределения. Числовые характеристики.

Случайной величиной называется переменная величина, которая в результате опыта может принимать то или иное числовое значение. Рассмотрим случайную величину , возможные значения которой образуют конечную или бесконечную последовательность чисел x₁, x₂, ..., x_n, ... . Пусть задана функция p(x), значение которой в каждой точке x=x_i (i=1,2, ...) равно вероятности того, что величина примет значение x_i:

Такая случайная величина называется дискретной (прерывной).

Рядом распределения дискретной случайной величины называется таблица, в верхней строке которой перечислены в порядке возрастания все возможные значения Х: х₁, х₂,…, х_n, а в нижней строке – вероятности этих значений: p_i = P(X=x_i)

Ряд распределения случайной величины Х записывается в виде таблицы:

Числовые характеристики – числа, которые характеризуют различные свойства случайных величин.

М атематическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.

С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Д исперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

σ = + SQR(D[x])

Модой М₀ дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

Медианой MD случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

Начальным моментом порядка k случайной величины Х называется математическое ожидание величины Х^k

Для дискретной случайной величины:

Для непрерывной случайной величины:

Начальный момент первого порядка равен математическому ожиданию.

Центральным моментом порядка k случайной величины Х называется математическое ожидание величины

Для дискретной случайной величины:

Для непрерывной случайной величины:

Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.

А бсолютный начальный момент:

Абсолютный центральный момент:

Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.