16.A. Сіметрычная група. Раскладанне падстановы ў здабытак незалежных цыклаў (без доказу). Парадак падстановы. Цотнасць падстановы (без доказу карэктнасці азначэння цотнасці). Зменназнакавая група.

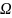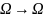Няхай непустое мноства. Мноства усіх біекцыяў ёсць группа ў дачыненні да аперацыі множання адлюстраванняў 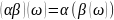, для 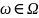- сіметрычная група мноства .

Яе элементы наз. падстановамі мноства .

Калі - канцоўнае мноства прадку n, тады таксама абазначаюць 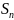і наз. сіметрычная група ступені n.

Падстанову абазначым 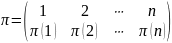. З таго, што 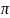- падстанова, г.зн. біекцыя вынікае – перастаўленне лікаў 1,2,…,n. Значыць лікі 1,2,…,n сустракаюцца адзін і толькі aдзін раз.

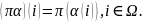
Тэарэма1: Парадак групы роўны n! .

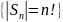Азн.1: Падстановы 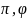наз. незалежнымі, калі

.

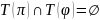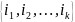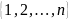Азн.2: Няхай - падстанова з k элементаў мноства = . Падстанова

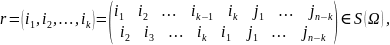
дзе 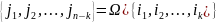, наз. цыклам даўжыні k.

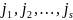Азн.3: Цыклы ( ) і ( ) наз. незалежнымі ці неперасякальнымі, калі 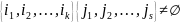. Незалежныя цыклы перастановачныя.

Тэарэма2: Адвольная падстанова 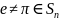раскладаецца ў здабытак незалежных цыклаў даўжыні, больш за 1. Гэты расклад адназначны з дакладнасцю да парадку сумножніка.

Вынік1: Парадак падстановы роўны найменшаму супольнаму кратнаму даўжыняў незалежных цыклаў, якія ўваходзяць у расклад .

Азн.4: Цыкл даўжыні 2 наз. транспазіцыяй.

Вынік2: Кожная падстанова з раскладаецца ў здабытак транспазіцыяў.

Азн.5: Функцыя f(x₁,x₂,…,x_n), вызначаная на камутатыўным колцы, наз. косасіметрычнай, калі r f=-f для адвольнай транспазіцыі r .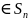

Лема: Няхай 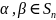. Тады .

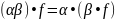Тэарэма3: Няхай , 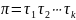– некаторы расклад у здабытак транспазіцыяў. Тады цотнасць ліку k цалкам вызначаецца падстановай і не залежыць ад раскладу .

Азн.6: Падстанова наз. цотнай, калі яна раскладацца ў здабытак цотнай колькасці транспазіцыяў, і няцотнай, калі яна раскладаецца ў здабытак няцотнай колькасці транспазіцыяў.

Вынік: Усе цотныя падстановы ступені складаюць падгрупу 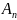групы парадку .

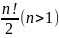Група наз. зменназнакавай групай ступені n.

18.A. Ізамарфізмы групаў. Азначэнне, прыклады, уласцівасці.

Азн.1: Няхай G і 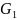- групы з аперацыямі • і * адпаведна. Біекцыйнае адлюстраванне наз. ізамарфізмам групы G у групу , калі для адвольных элементаў 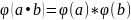. (1)

Калі існуе некаторы ізамарфізм , будзем казаць, што група ізаморфная групе і пісаць .

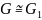Аперацыя ў G і наз. множаннем і замест (1) будзем пісаць: .

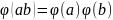Уласцівасці ізамарфізмаў групаў:

1. Для адвольнай групы G тоеснае адлюстраванне 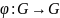– ізамарфізм;

2. Калі - ізамарфізм групаў, тады – таксама ізамарфізм;

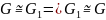
3. Калі , 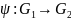- ізамарфізмы групаў, тады 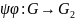– таксама ізамарфізм.

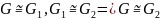
З гэтых уласцівасцей вынікае, што дачыненне ізамарфізмаў ёсць дачыненне эквівалентнасці на мностве ўсіх групаў і таму мноства ўсіх групаў падзяляецца на неперасякальныя класы ізаморфных паміж сабой групай.

Азн.2: Ізамарфізм групы на сябе наз. аўтамарфізмам групы .

Тэарэма1: Aut G – група ў дачыненні да аперацыі множання аўтамарфізмаў.

Тэарэма2: 1) Адвольная бясконцая цыклічная група ізаморфная адытыўнай групе цэлых лікаў Z;

2) Адвольная канцоўная цыклічная група парадку n ізаморфная C(n) камплексных каранёў ступені n з 1.

Тэарэма3(Кэлі): Адвольная канцоўная група парадку n ізаморфная некаторай падгрупе сіметрычнай групы S_n.

Вынік: З дакладнасцю да ізамарфізму існуе толькі канцоўная колькасць групаў фіксаванага парадку n.

Прыклады:

1) Разгледзім групу Z у дачыненні да складання і групу цотных лікаў – (2) і вызначым адлюстраванне : 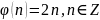відавочна - біекцыя.

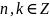
Пакажам, што захоўвае аперацыю: 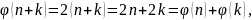значыць - ізамарфізм групаў .

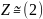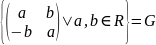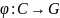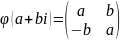2) Разгледзім адытыўную групу C і адытыўную групу матрыцаў . Вызначым адлюстраванне : - ізамарфізм групаў.