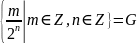- •1.A. Бінарныя алгебрычныя аперацыі. Асацыятыўныя, камутатыўныя аперацыі; нейтральны элемент, сіметрычны элемент. Азначэнні, прыклады, ўласцівасці.
- •2.A. Колца, поле. Азначэнні, прыклады, ўласцівасці. Два крытэры падколца. Два крытэры падполя.
- •3.A. Параўнанні. Колца рэштаў. Абарачальныя элементы колца рэштаў.
- •4.A. Ідэал колца. Азначэнне, прыклады, крытэр ідэалу.
- •8.A. Ізамарфізмы і гомамарфізмы колцаў. Азначэнні, прыклады, уласцівасці.
- •14.A. Група. Азначэнне, прыклады, уласцівасці. Два крытэры падгрупы.
- •15.A. Спараджальнае мноства (сістэма ўтваральных) падгрупы. Цыклічная група. Падгрупы цыклічнай групы.
- •16.A. Сіметрычная група. Раскладанне падстановы ў здабытак незалежных цыклаў (без доказу). Парадак падстановы. Цотнасць падстановы (без доказу карэктнасці азначэння цотнасці). Зменназнакавая група.
- •18.A. Ізамарфізмы групаў. Азначэнне, прыклады, уласцівасці.
- •22.A. Гомамарфізмы групаў. Азначэнне, прыклады, уласцівасці.
- •24.A. Колца паліномаў ад некалькіх зменных. Лексікаграфічны запіс паліномаў.
- •25.A. Сіметрычныя паліномы. Формулы Віета. Асноўная тэарэма пра сіметрычныя паліномы (без доказу).
- •28.A. Тэарэмы Ойлера, Фэрма і Вільсана (без доказаў).
- •30.A. Тэарэма пра існаванне кораня (без доказу). Поле раскладу паліному.
- •32.A. Алгебрычныя і трансцэндэнтныя элементы. Поле алгебрычных элементаў. Алгебрычная замкнёнасць поля алгебрычных лікаў (без доказаў).
- •36.A. Асноўная тэарэма алгебры камплексных лікаў (без доказу).
14.A. Група. Азначэнне, прыклады, уласцівасці. Два крытэры падгрупы.
Азн.1:
Непустое
мноства
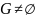 ,
на
якім вызначаны бінарная алгебрычная
аперацыя •, наз. групай , калі выконваюцца
наступныя аксіёмы:
,
на
якім вызначаны бінарная алгебрычная
аперацыя •, наз. групай , калі выконваюцца
наступныя аксіёмы:
Аперацыя • асацыятыўная, г.зн.
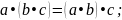
Існуе нейтральны элемент
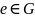 у дачыненні да аперацыі
•,
г.зн. такі элемент, што
у дачыненні да аперацыі
•,
г.зн. такі элемент, што
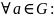
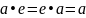 ;
;
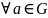 існуе
сіметрычны элемент, г.зн. такі элемент
існуе
сіметрычны элемент, г.зн. такі элемент
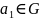 што
што
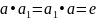 .
.
Множанне – мультыплікатыўная група.
Складанне – адытыўная група.
Прыклады:
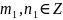
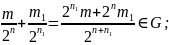
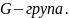
2)
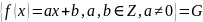
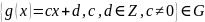
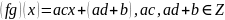

Азн.2: Падмноства H групы G наз. падгрупай групы G, калі H –група ў дачыненні да аперацыяў, вызначаных ў G. Абазначаецца H<G.
Азн.3:
Група
G
наз.
абэлевай (камутатыўнай), калі аперацыя
ў G
камутатыўная, г.зн.
 для
для
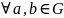 .
.
Азн.4: Група наз. канцоўнай, калі ў ёй канцоўная колькасць элементаў. Колькасць элементаў у канцоўнай групе G наз. парадкам групы і абазначаецца │G│.
Уласцівасці групаў:
Для адвольных элементаў
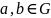 кожнае
з раўнанняў ах=
кожнае
з раўнанняў ах=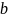 і
уа=
мае
ў
і
уа=
мае
ў
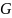 адзіны
развязак
адзіны
развязак
х=а-1 і у= а-1 адпаведна;
Для адвольных (ab)-1=b-1a-1;
Адзінка падгрупы H групы G ёсць адзінка групы G;
У групе G толькі адна адзінка. Для кожнага элементу з G ёсць толькі адзін адваротны элемент.
Тэарэма1(1 крытэр падгрупы): Непустое падмноства H групы G ёсць падгрупа групы G к.і т.к :
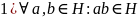 .
.
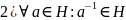
Тэарэма2(2
крытэр падгрупы):
Непустое падмноства H
групы G
ёсць падгрупа групы G
к.і
т.к для
адвольных
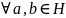 элемент
элемент
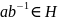 .
.
15.A. Спараджальнае мноства (сістэма ўтваральных) падгрупы. Цыклічная група. Падгрупы цыклічнай групы.
Сцв.1: Перасячэнне адвольнага мноства падгрупаў групы G ёсць падгрупа групы G.
Азн.1:
Няхай
M
падмноства групы G,
перасячэнне ўсіх падгрупаў групы G,
якія змяшчаюць мноства
M,
будзем абазначаць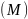 і наз. падгрупай спароджанай мноствам
M,
а само M
наз. спараджальным мноствам (ці мноствам
утваральных) падгрупы (M).
і наз. падгрупай спароджанай мноствам
M,
а само M
наз. спараджальным мноствам (ці мноствам
утваральных) падгрупы (M).
Відавочна
(M)
ёсць найменшая падгрупа групы G,
якая змяшчае M,
г.зн. калі
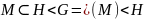 .
.
Тэарэма1:
Няхай
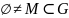 .
Падгрупа спараджальная
.
Падгрупа спараджальная
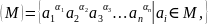
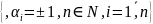 .
.
Азн.2: Група, спароджаная адным элементам наз. цыклічнай.
Азн.3:
Найменшы
натуральны
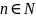 ,
які
адпавядае ўмове
,
які
адпавядае ўмове
 ,
наз. парадкам элементу
,
наз. парадкам элементу
 .
.
Калі
для кожнага

 ,
тады a
наз. элементам бясконцага парадку.
,
тады a
наз. элементам бясконцага парадку.
Абазначаецца
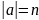 .
.
Тэарэма2:
1) Калі
- элемент
парадку
,
тады
група (
)
– канцоўная парадку
і
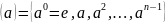 .
.
2)
Калі
- элемент
бясконцага парадку,
тады
група (
)
– бясконцая і
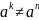 для n≠k
n,k
для n≠k
n,k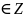 .
.
Заўвага:
Калі
- элемент
парадку
,
тады
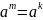
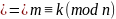 .
.
У
прыватнасці
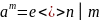 .
.
Тэарэма3: Кожная падгрупа цыклічнай групы -цыклічная.
Сцв.2:
Няхай
.
Для адвольнага
k
парадак
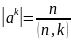 .
.
Сцв.3: У цыклічнай групе парадку n, для адвольнага натуральнага k, k | n існуе адзіная падгрупа парадку k.
Тэарэма 5: 1) Адвольная бясконцая цыкічная група ізаморфная адытыўнай групе Z;
2) Адвольная канцоўная цыклічная група парадку n ізаморфная групе C(n) камплексных каранёў ступені n з адзінкі.