1. A. Бінарныя алгебрычныя аперацыі. Асацыятыўныя, камутатыўныя аперацыі; нейтральны элемент, сіметрычны элемент. Азначэнні, прыклады, ўласцівасці.

2. A. Колца, поле. Азначэнні, прыклады, ўласцівасці. Два крытэры падколца. Два крытэры падполя.

3.A. Параўнанні. Колца рэштаў. Абарачальныя элементы колца рэштаў.

4. A. Ідэал колца. Азначэнне, прыклады, крытэр ідэалу.

8. A. Ізамарфізмы і гомамарфізмы колцаў. Азначэнні, прыклады, уласцівасці.

14. A. Група. Азначэнне, прыклады, уласцівасці. Два крытэры падгрупы.

15. A. Спараджальнае мноства (сістэма ўтваральных) падгрупы. Цыклічная група. Падгрупы цыклічнай групы.

16. A. Сіметрычная група. Раскладанне падстановы ў здабытак незалежных цыклаў (без доказу). Парадак падстановы. Цотнасць падстановы (без доказу карэктнасці азначэння цотнасці). Зменназнакавая група.

18. A. Ізамарфізмы групаў. Азначэнне, прыклады, уласцівасці.

22. A. Гомамарфізмы групаў. Азначэнне, прыклады, ула-ці.

24. A. Колца паліномаў ад некалькіх зменных. Лексікаграфічны запіс паліномаў.

25. A. Сіметрычныя паліномы. Формулы Віета. Асноўная тэарэма пра сіметрычныя паліномы (без доказу).

28. A. Тэарэмы Ойлера, Фэрма і Вільсана (без доказаў).

30. A. Тэарэма пра існаванне кораня (без доказу). Поле раскладу паліному.

32. A. Алгебрычныя і трансцэндэнтныя элементы. Поле алгебрычных элементаў. Алгебрычная замкнёнасць поля алгебрычных лікаў (без доказаў).

36. A Асноўная тэарэма алгебры камплексных лікаў (без доказу).

1.A. Бінарныя алгебрычныя аперацыі. Асацыятыўныя, камутатыўныя аперацыі; нейтральны элемент, сіметрычны элемент. Азначэнні, прыклады, ўласцівасці.

Азн.1:Няхай Х-непустое мноства.Будзем казаць, што на мностве Х вызначана бінарная алгебрычная аперацыя, калі кожнай спарадкаванай пары (a,b) элементаў мноства Х пастаўлены ў адпаведнасць адназначна вызначаны элемент з мноства Х.

Такім чынам, бінарная алгебрычная аперацыя на мностве Х – гэта f: Х Х Х.

Вобраз пары (а,b) f(а,b) будзем называць кампазіцыяй элементаў а,b і абазначаць а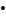 b.

Калі аперацыя на мностве называецца множаннем (складаннем), тады кампазіцыю а b будзем называць здабыткам (сумай) і абазначаць аb (а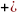 b).

Прыклады бінарных алгебрычных аперацыяў:

1) Складанне і множанне на мноствах: N, Z, Q, R, C, R[x], R_n*n

2) Адыманне на мноствах: Z, Q, R, C, R[x], R_n*n

3) Дзяленне на мноствах: Q^*= Q\{0}, R^*= R\{0}, C^*= C\{0}.

Азн.2:Будзем казаць, што элемент n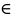 Х з’яўляецца нейтральным у дачыненні да бінарнай алгебрычнай аперацыі , калі для кожнага а Х, а n= n а= a.

Прыклады:

_{1) Для мностваў} Z, Q, R, C нейтральны элемент у дачынненні да аперацыі: складання - 0, множання – 1.

2) _Для R[x] нейтральнымі элементамі у дачынненні да складання і множання будуць адпаведна нулявы паліном і паліном нулявой ступені, роўны 1.

_{3) Для} R_n*n нейтральным элементам у дачынненні да складання і множання служаць нулявая і адзінкавая матрыцы.

_Сцв.1: Для адвольнай бінарнай алгебрычнай аперацыі не больш за адзін нейтральны элемент.

_{Азн.3:Бінарная алгебрычная аперацыя на мностве Х наз. асацыятыўнай, калі для адвольнага a,b,c X, a (b c)=(a b) c.}

Сцв.2: Калі бінарная алгебрычная аперацыя асацыятыўна, тады для адвольных натуральных n и i, 1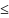 i n:

(a₁ a₂ 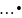a_i) (a_i+1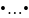 a_n) = a₁ a₂ a_n.

_{Азн.4:Няхай на мностве Х вызначана бінарная алгебрычная аперацыя ,якая мае нейтральны элемент n. Элемент а1} Х наз сіметрычным да элементу а Х у дачыненні да аперацыі _{, калі a а1=а1 а=n.}

_{Калі а1 -} сіметрычным да элементу а, тады а -сіметрычным да элементу а₁.

Сцв.3: Калі бінарная алгебрычная аперацыя на мностве Х асацыятыўна, тады для кожнага а Х існуе не больш за адзін сіметрычны элемент.

_{Калі аперацыя называецца множаннем, тады} сіметрычны да а элемент называюць адваротным і абазначаюць а^-1, калі аперацыя называецца складаннем, тады сіметрычны да а элемент называюць супрацьлеглым і абазначаюць -а.

_Азн.5: Бінарная алгебрычная аперацыя на мностве Х, наз. камутатыўнай, калі для адвольных элементаў _{a,b X:}

_{a b=b a.}

_{Прыклады:}

_{1) Аперацыі “+” і “*” на мноствах Z, Q, R, C, R[x] – камутатыўныя.}

_{2) На} R_{n*n “+” – камутатыўнае, а “*” для n>1 – некамутатыўнае.}

2.A. Колца, поле. Азначэнні, прыклады, ўласцівасці. Два крытэры падколца. Два крытэры падполя.

Азн.1: Непустое мноства R≠Ø, на якім вызначаны бінарныя алгебраічныя аперацыі складання і множання, наз. колцам, калі выконваюцца наступныя аксіёмы:

1.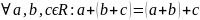 – асацыятыўнасць складання;

2. ;

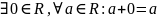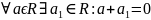
3. 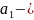процілеглы да элементу а;

4.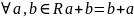 - камутатыўнасць складання;

5.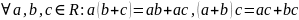 – дыстрыбутыўнасць;

6.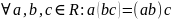 – асацыятыўнасць множання.

1)-4) у дачынненні да “+”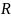 - абэлева група.

Азн.2: Колца R наз. камутатыўным, калі

.

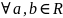
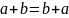Азн.3: Колца R наз. колцам з адзінкаю, калі ,

.

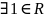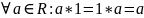Азн.4: Непустое мноства К колца R наз. падколцам колца R, калі К ёсць колца ў дачын. да аперацыяў, вызначаных ў R.

Азн.5: Камутатыўнае колца F з адзінкаю наз. полем, калі ў ім больш за адзін элемент (|F |>1) і

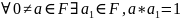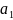, - адваротны да а.

Азн.6: Непустое падмноства Р поле 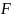наз. падполем поля , калі Р ёсць поле ў дачыненні да аперацыяў, вызначаных у .

– пашырэнне поля Р.

Тэарэма 1 (першы крытэр падколца): Непустое падмноства К поле з’яўл. падколцам колца R к.і т.к. выконваюцца наступныя ўмовы:

;

.

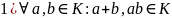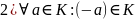Тэарэма 2 (другі крытэр падколца): Непустое падмноства К поле з’яўл. падколцам колца R к.і т.к. выконваюцца ўмовы: .

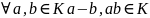Тэарэма 3 (першы крытэр падполя): Падмноства Р поля F, у якім больш за адзін элемент, з’яўл. падполем поля F, к.і т.к.:

1. P – падколца F;

2. .

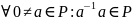Тэарэма 4 (другі крытэр падполя): Падмноства Р поля F |P|>1, з’яўл. падполем поля F к.і т.к.:

1. ;

2. .

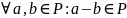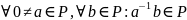Прыклад:

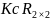1. – колца

2. С – поле у дачыненні да “+” і “*”

3. С – пашырэнне поля , а - пашырэнне Q

4. Z – не поле

5. Мноства R[x] усіх паліномаў над R – камутатыўнае колца з адзінкаю у дачынені да “+” і “*” , але не поле

6. Цотныя лікі у дачыненні да “+” і “*” з’яўляюцца калцам.