13.A. Вынікі з тэарэмы дэдукцыі і сцверджанне: Адвольная тэарэма злічэння выказванняў ёсць таўталогія. Несупярэчлівасць злічэння выказванняў.

Вынік1: для адвольных формулаў А,В,С злічэнне выказваняў А  В, В С |-А  С. Вынік2: для адвольных формул А,В,С з злічэнняу выказванняў А (В  С), В|-А  С. Вынік3: Няхай А₁, А₂,…,А_к ,В- формулы, (К>=1).

А₁, А₂,…,А_к |- В к. і. т. к

|- А₁  (А₂  … (А_к-1  (А_к  В))…) Сцв.2: адвольная тэарэма злічэняў. выказванняў ёсць тауталогія. Вынік1: злічэнне выказванняў несупярэчлівае , г зн, не існуе формулы А такой, што А і  А -тэарэмы L. Сцв1.(тэарэма дэдукцыі) Калі Г-мноства формулаў, А і В –формулы і Г, А|-В, тады Г|-АВ

17.A. Тэарэма пра поўнасць (без доказу). Вынікі.

Сцв3.(тэарэма пра поўнасць) Калі формула А злічэння выказванняу з*яуляецца. тауталогіей, тады яна ёсць тэарэма тэорыі L. Вынік1: Няхай выраз В мае знакі- , , , ,  і з*яул. скарачэннем пэунай формулы А тэорыі L.

В з*яул. тауталогіей к і т к А ёсць тэарэма тэорыі L. Вынік2: Няхай А₁,…,А_к ,В -формулы тэорыі L. А₁,…,А_к |-В к .і. т. к А₁,…,А_к |=В. Вынік3:Злічэнне выказванняў, развязальная тэорыя.

19.A. Прэдыкаты. Тоесна праўдзівыя, тоесна непраўдзівыя, здзяйсняльныя прэдыкаты. Раўназначныя прэдыкаты. Прыклады. Аперацыі над прэдыкатамі. Геаметрычная інтэрпрэтацыя аперацыяў над прэдыкатамі.

Азн.1: Няхай М₁,..,М_n ≠Ø n-месцавым прэдыкатам на М₁,..,М_n n наз функцыя ад n аргументаў Р(х_1,.., х_n), дзе

х_і М_і , і =1,n , а значэнні функцыі Р(х_1,.., х_n) ёсць выказванне .

Азн.2: Няхай Р(х_1,.., х_n) на мноствах М₁,..,М_n наз:

1)тоесна праўдзівым, калі для кожнага набору значэнняў аргументаў, ягонае значэнне роўнае 1.

2)тоесна непраўдзівым,калі для кожнага набору значэнняў аргументаў ягонае значэнне роўнае 0.

3)здзяйсняльным, калі існуе прынамсі адзін набор значэнняў аргументаў,для якога ягонае значэнне роўнае 1.

Р(х_1,.., х_n)=1 Р(х_1,.., х_n)=0

Азн.3: Прэдыкаты Р(х_1,.., х_n) і Q(х_1,.., х_n) на мноствах М₁,..,М_n наз раўназначнымі , калі іхнія мноства праўдзівасці роўныя. Р(х_1,.., х_n) == Q(х_1,.., х_n)

Прыклад: Прэдыкаты Р(х)=(х-1=0), Q(х)=(х²-2х+1=0)

S(х)=(х³-3х²+3х-1=0) рауназначныя на R,C мноства праўдзівасці {1}

1) Р(х_1,.., х_n) Q(х_1,.., х_n)- | n=2 М₁=М₂=R

n-месцавы прэдыкат на М₁,..,М_n

Р(х_1,.., х_n) S (х_1,.., х_n) А_Sc М₁*..*М_n

А_Р=А_р=( М₁*..*М_n )\ А_р

2) Р(х_1,.., х_n)  Q(х_1,.., х_n)

А_РQ= А_рА _Q

3) Р(х_1,.., х_n)  Q(х_1,.., х_n)

А_Р_Q= А_рА _Q

А_Р=А_р, А_РQ= А_рА _Q , А_Р_Q= А_рА _Q

4) Р(х_1,.., х_n)  Q(х_1,.., х_n)==

== Р(х_1,.., х_n) Q(х_1,.., х_n)

А_РQ= А_рА _Q

5) А_РQ

20.A. Формулы логікі прэдыкатаў. Інтэрпрэтацыя формулы. Раўназначнасць формулаў. Логікава агульназначныя формулы логікі прэдыкатаў. Лагічная выснова мноства формулаў. Прыклады.

Азн.1: х₁,х₂,х₃,… - злічонае мноства прадметных зменных, а₁,а₂,а₃,… - мноства прадменых канстант, А₁¹,А₁²,.. ,А_k^j, - мноства прэдыкатных літараў,

f₁¹,f₁²,.. ,f_k^j, - мноства функцыянальных літараў.

Верхні індэкс прэдыкатных і функцыянальных літараў паказвае колькасць аргументаў ,а ніжні служыць для адрозніння літараў з аднолькавай колькасцю аргументаў .

Азн.2: (а)Усякая прадметная зменная і прадметная канстанта ёсць тэрм;

(б)Кал f_iⁿ - функцыянальная літара, t₁,.. ,t_n - тэрмы, тады f_iⁿ (t₁,.. ,t_n) - тэрм;

(в)Выраз з'я ляецца тэрмам толькі калі гэта вынікае з (а),(б).

Азн.3: Няхай A_iⁿ - прэдыкатная літара, t₁,..,t_n - тэрмы, то A_iⁿ ( t₁,.. ,t_n) - элементарная формула.

Азн.4 (а)Усякая элементарная формула ёсць формула логікі прэдыкатаў .;

(б)кал А і В – формулы логікі прэдыкатаў, х_і - прадметная зменная, тады ( А),( АВ),( АВ),( А=>В ), (А<=>В ),( 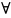х_і А),( 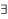х_і А) - формулы логікі прэдыкатаў; (в)Іншых формулаў няма

Няхай А – адвольная формула логікі прэдыкатаў,

М ≠Ø. Замяняючы ў формуле А прадметныя канстанты на фіксаваныя элементы мноства М, прэдыкатныя і функцыянальныя літары на фіксаваныя прэдыкаты і функцыі ад той самай колькасці зменных на мностве М, атрымаем прэдыкат на мностве М, ад вольных зменных формулы А. такая канструкцыя наз інтэрпрытацыя формула А на мностве М.

Азн.5: Формулы А і В логікі прэдыкатаў наз

раўназначнымі на мностве М, калі пры адвольнай інтэрпрытацыі на М яны ператвараюцца ў

раўназначныя прэдыкаты.

Азн.6: Формулы А і В логікі прэдыкатаў наз раўназначнымі (логікава эквівалентнымі ), калі яны

раўназначныя на адвоьным мностве М.

Азн.7: Няхай А –формула логікі прэдыкатаў, М ≠Ø. Формула А наз М-агульназначнай (тоесна праўдзівай на мностве М), калі пры адвольнай інтэрпрытацыі на М яна ператвараецца ў тоесна праўдзівы прэдыкат на М.

Азн.8: Формула А логікі прэдыкатаў , наз логікава агульназначнай (тоесна праўдзівай),калі яна тоесна праўдзівая на адвольным мностве М.

Азн.9: Формула В логікі прэдыкатаў наз логічнай высновай (логікавым вынікам) формулаў {А₁,..,А_m }, калі ў кожнай інтэрпрытацыі на адвольным мностве для ўсякага набору значэнняў зменных, для якога кожная А_і мае логікавая значэнне 1 формула В таксама мае значэнне 1 А₁,..,А_m |=В

23.А. Дастасаванне алгебры выказванняу і логікі прыдыкатау да натуральнай мовы. Пры перакладе з натуральнай мовы на мову логікі прыдыкатау трэба выбраць прыдатнае мноства і інтэрпрытацыі на гэтым мностве. Прыклад 1: а) экзаменатар паставіу “4” і Каця заплакала б)Каця заплакала, і экзаменатар паставіў “4”

Прыклад2.а)Я абяцаў вам зрабіць гэта, але я баюся

Б)Я баюся,але я абяцаў вам зрабіць гэта

Часам у натуральнай мове слова “некаторыя” мае адтенне “некаторыя, але не усе” Слове “усе”, “кожны”, “адвольны”, “існуе”, “некаторы”. У жывой мове прапускаюцца. Чалавек падауся на Эверэст.

3 B. Правіла падстановы. Адмаўленне да прапазіцыйнай формулы, якая змяшчае , , l. Прынцып дуальнасці (без доказаў).

6 B. Прапазіцыйныя формулы і булевы функцыі. Поўныя сістэмы злучнікаў (без доказу тэарэмы). ДНФ і КНФ. Кан'юнкцыя адмаўленняў і штрых Шэфера.

10 B. Лема:├ А 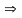А для адвольнай формулы A.

11 B. Тэарэма дэдукцыі (без доказу). Вынікі.

14 B. Лема 2 для тэарэмы пра поўнасць.

15 B. Лема 3 для тэарэмы пра поўнасць (без доказу).

21 B. Прыведзеная нармальная форма формулы логікі прэдыкатаў.