22. Лопиталь ережесі. Тейлор формуласы. Кейбір функ-ды Тейлор форм-сы бойынша жіктеу

Лопиталь ережелерін пайдаланып, туынды көмегімен анықталмағандықтарды аша аламыз.

Теорема (Лопиталь ережесі): Егер x₀ нүктесінің аймағында анықталған функциялары осы аймақта дифференциалданса және 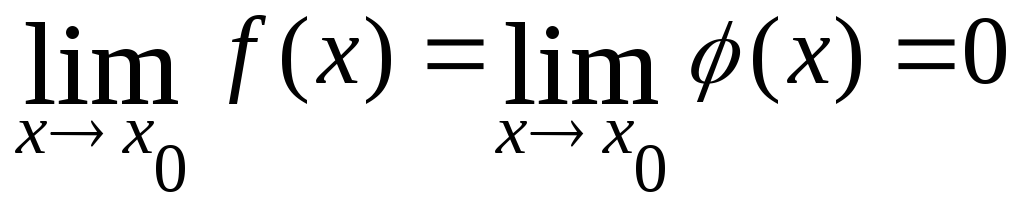, , - бар болса, онда - шегі бар болып, = теңдігі орындалады.

Дәлелдеуі. функциялары Коши теоремасының шарттарын қанағаттандырады. Сондықтан болғандықтан функцияның үзіліссіздігінен болады. Егер х₀ бар болса, онда деп аламыз. Егер , онда . Осыдан .

Ескерту: 1) Теореманы бір жақты шектерді табуға да қолдана аламыз.

2) Лопиталь ережесін ізделінді шекті табу үшін бірннеще ретқолдануға болады.

3) Ізделінлі шек бар болса да, туындылардың қатынасының шегі болмауы мүмкін.

Теореманы х → ∞ жағдайында да қолдана аламыз.

Тейлор формуласын математикада кеңінен пайдаланады.

Тейлор теоремасы: f(x) функциясының a нүктесінің берілген бір аймағында (n+1)- ретті туындысы бар болсын. Егер x-нүктесі осы аймақта жатса, онда (a, x) интервалында С нүктесі табылып,

(1) теңдігі орындалады.

Дәлелдеуі.

Теоремадағы берілген аймақта f(x) және оның n-ретке дейінгі барлық туындылары осы аймақта үзіліссіз және дифференциалданады. деп (1) формуладағы бірінші n мүшелердің қосындысын белгілейік, яғни Бұл өрнек n дәрежелі Тейлор көпмүшелігі, ал (1) формуласы Тейлор формуласы делінеді. деп белгілейік. Егер теңдігін көрсетсек, теорема дәлелдендi.

Енді [a, x] сегментіндегі t нүктені алып, мына көмекші функцияны қарастырайық: (2)

F(t) функциясы [a, x] сегментінде Ролль теоремасының барлық шарттарын қанағаттандырады.

1) f(x) және оның барлық n туындылары [a,x] сегментінде дифференциалданатындықтан, F(t) [a, x]- те үзіліссіз және дифференциалданады және

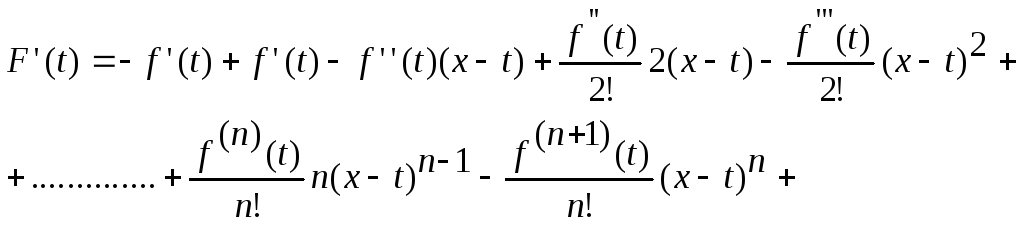
(3)

2)

Ролль теоремасы бойынша c (a, x) табылып, F’(c)=0 болады, яғни . Осыдан (4). Теорема дәлелденді.

Формула (4) - Тейлор формуласының Лагранж формадағы қалдық мүшесі делінеді.

c (a, x) болғандықтан, түрінде жаза аламыз. Сондықтан (5) . Қалдық мүшенің бұл түрі жиі қолданылады.

Егер a=0 болса, онда (1) формула былай жазылады:

(5) мұнда

Маклорен формуласы делінеді және ол Тейлор формуласының дербес жағдайы болады.

23. Экстремумның бар болуының жеткілікті шарты

Теорема 1. (экстремумның жеткілікті шарты): Егер үзіліссіз функцияның туындысы кризистік нүктеден өткенде таңбасын ауыстырса, онда ол нүктеде экстремум бар болады. x₀ нүктесінің сол жағынан оң жағына өткенде f’(x) таңбасы “+”-тен “ - ”-ке өзгерсе, онда максимум нүктесі, ал егер “-”-тен “+”–ке өзгерсе – минимум нүктесі болады.

Дәлелдеу. x₀ кризистік нүкте болсын. f’(x)>0 интервалында, ал f’(x)<0 интервалында делік. Лагранж теоремасы бойынша f(x)-f(x₀)>f’(c)(x-x₀); интервалында f’(c)>0, ал x - x₀< 0 болғандықтан f(x) < f(x₀). интервалында f’(c)<0, x - x₀ > 0. Сондықтан f(x)<f(x₀). Осыдан интервалында f(x)<f(x₀) . x₀ – максимум нүктесі. Осылайша теореманың екінші тұжырымы дәлелденді.

Теорема 2(экстремумның жеткілікті шарты) f(x) функциясы x₀ нүктесінің аймағында анықталсын. Егер f’(x₀) = f’’(x₀)…….f^{( k – 1 )}(x₀), ал f^(k)(x₀)≠0 болса, онда k-жұп және f^(k)(x₀)<0 болғанда x₀ нүктесінде максимум болады, ал k-жұп, f^(k)(x₀)>0, x₀-минимум нүктесі болады. Егер k-тақ болса, x₀ нүктеде экстремум болмайды.

Дәлелдеуі. x₀ нүктесінің аймағында f(x) функциясын Тейлор формулaсымен өрнектейік. , мұнда Осыдан . үзіліссіз болғандықтан таңбасы x₀-аймағында таңбасымен бірдей болады. Сондықтан k-жұп болғанда және f^(k)(x₀)>0 болса, онда f(x)-f(x₀)>0, , яғни f(x)>f(x₀), x₀-минимум нүктесі. Егер k-жұп, ал < 0 болса, онда f(x)-f(x₀) < 0, яғни х₀-максимум нүктесі. Егер k-тақ және >0 болса, онда f(x) < f(x₀) -сол жағы, f(x)>f(x₀) -оң жағы. Осылайша x₀ нүктесінде экстемум жоқ, < 0 болғанда да x₀ нүктеci экстремум болмайды.

24.Ф-ның ойыстық ж-е дөңестік шарттары. Ф-ның иілу нүктесі

(a,b) интервалында анықталған функциясы осы интервалда ойыс деп аталады, егер (a,b) интервалының кез-келген нүктелері мен қосындысы бірге тең кез-келген сандары үшін

(1)

теңсіздігі орындалса.

Егер және болса, онда бұл теңсіздік қатаң теңсіздікке айналады және функция (a,b) интервалында қатаң ойыс деп аталады.

Егер функциясы үшін (1) теңсіздік керісінше болса, онда функция (a,b) интервалында дөңес немесе (a,b) интервалында дөңестігі жоғары деп аталады. Осыған байланысты ойыс функцияны кейде дөңестігі төмен деп те атайды.

Ойыстықтың геометриялық сипаты: функция графигі доғасының кез-келген нүктесі осы доғаны керуші хорда нүктелерінің астында жатады.

Шынында да, (1) теңсіздіктің сол жағында f(x) функциясның нүктесіндегі мәні, ал оң жағында нүктелерінен өтетін сызықтық функцияның нүктесіндегі мәні (суретті қара).

Барлық қарастыру дөңестігі төмен бағытталған және дөңестігі жоғары бағытталған функциялар үшін бірдей болғандықтан, біз келешекте тек ойыс функциялармен ғана айналысамыз. Ал дөңес функцияларды дәл солай тек шарттарын сәйкес өзгертіп қарастыра беруге болады.

Егер (1) теңсіздікте десек, онда осы

түрінде, ал немесе болса, оны

түрінде жазуға болады. Бұдан болғандықтан, теңсіздігін қанағаттандыратын кезкелген үшін (2)

теңсіздігін аламыз. Бұл функция ойыстығының басқаша жазылуы. Бұл нүктелерін қосатын І хорданың бұрыштық еселеуішінің нүктелерін қосатын ІІ хорданың бұрыштық еселеуішінен артпайтынын көрсетеді.

1-теорема (функцияның интервалда ойыстық критериі). (a,b) интервалында дифференциалданатын функциясының осы интервалда ойыс (дөңес) болуы үшін оның туындысының осы интервалда кемімейтін (өспейтін) болуы қажетті және жеткілікті.

Дәлелдеуі. Қажеттілігі. f функциясы (a,b) интервалында ойыс болса, онда (2) теңсіздік орындалады. Ал функциясы (a,b) интервалында дифференциалданатын болғандықтан, (2) теңсіздікте және жеке- жеке ұмтылдырып,

теңсіздіктерін аламыз. Бұл f(x) функциясы туындысының монотондылығын көрсетеді.

Енді қатаң ойыс функция үшін Лагранж теоремасын пайдаланып, болғанда

теңсіздіктерін аламыз. Бұл қатаң ойыс функция үшін туындының қатаң монотонды функция екенін көрсетеді.

Сонымен, дифференциалданатын функциясы (a, b) интервалында ойыс болса, онда туындысы бұл интервалда кемімейді, ал f қатаң ойыс болса, онда оның туындысы бұл интервалда өспелі болады.

Жеткіліктілігі. Айталық туындысы (a, b) интервалында кемімейтін болсын. Онда болғанда Лагранж теоремасы бойынша

теңдігін қанағаттандыратын нүктелері табылады. Ал болғандықтан (2) теңсіздік орындалады. Егер болса, онда қатаң ойыстық шығады.

Салдар. (a,b) интервалында екінші ретті туындысы бар функциясы осы интервалда ойыс болуы үшін оның екінші ретті туындысы осы интервалда теріс болмауы қажетті және жеткілікті. Егер болса, онда функциясы қатаң ойыс.

Дәлелдеуі. Дәлелдеуі осы теорема мен 16-параграфтың 1-ші теоремасынан шығады.

Жазықтықта функцияның ойыстық маңайының оның графигіне жүргізілген жанаманың бір жағында жату сипатын анықтайтын тағы бір тұжырымды келтірейік.

1-теорема. (a,b) интервалында дифференциалданатын функциясы осы интервалда ойыс (дөңес) болуы үшін оның графигінің нүктелері оған жүргізілген кез-келген жанама нүктелерінен төмен (жоғары ) жатпауы қажетті және жеткілікті. Сонымен бірге функцияның қатаң ойыс (дөңес) болуы үшін оның графигінің тек жанасу нүктесінен басқа барлық нүктелерінің жанама нүктелерінен жоғары (төмен) жатуы қажетті және жеткілікті.

Дәлелдеуі. Қажеттілігі. Егер болса, онда нүктесінде функция графигіне жүргізілген жанама теңдеуі

болғандықтан, Лагранж теоремасы бойынша

Ал f ойыс болғандықан оның туындысы (a,b) интервалында кемімейді және таңбасы таңбасымен бірдей, сондықтан

Егер қатаң ойыс болса, онда туындысы интервалында қатаң өседі, демек, және .

Жеткіліктілігі. Егер кез-келген нүктелері үшін

(1)

болса, онда

және

Сонда х₁<x<x₂ теңсіздіктерін қанағаттандыратын кез келген нүктелері үшін

(2)

теңсіздігін аламыз.

Егер (1) теңсіздік қатаң болса, онда (2) теңсіздік те қатаң болады. Бұл (2) теңсіздік 23-параграфтың функция ойыстығын анықтайтын (2) теңсіздігімен бара бар. Дөңестік жағдайы дәл осылай дәлелденеді. Теорема дәлелденді.

Мысалы, функциясы қатаң ойыс. Мұның графигіне (0,1) нүктесінде жүргізілген жанама теңдеуі y=x+1, өйткені . Сондықтан 1-теорема бойынша, егер болса, онда

Айталық нүк-нің -да анықтаған ж-е дифф-тын f(x) ф-сы берілсін. Егер -()= жиынында дөңес-ойыс болса онда ф-я гр-нің () нүктесі оның иілу нүктесі д.а.

25. Функция графигінің ассимптотасы

Егер және шектерінің ең болмағанда біреуі +∞ немесе -∞ болса онда х=а түзуі f(x) функциясы графигінң верцикаль ассимптотасы деп атайды.

Егер *(*(1) болса онда y=kx+b түзуі функциясы графигінің x->+∞(x->-∞) болғанда көлбеу ассимптотасы деп аталады.

Theorem: Егер y=kx+b түзуі x->+∞ x->-∞ ұмтылғанда ) функцсиясы графигінің көлбеу ассиптотасы болу үшін = k

= k (2)

Дәлелдеуі Қажеттілігі жағдайын дәлелдейміз айталық y=kx+b түзуі f(x) функцсясы графигінің ( көлбеу ассимптотасы болсын онда (1)-ші теңдіктерін = + k + және

=-b)+b теңдіктерін алып одан = k ,

Екенін көреміз

Жеткіліктілігі айталық (2) ОРЫНДАЛСЫН онда оның теңдігінен аламыз бұл y=kx+b түзуінің болғанда функциясың көлбеу ассимптотасы екенін көрсетеді theorema daleldendi! Ескерту кейде y=kx+b көлбку ассиптртасын k=0 болғанда горизанталь ассимптотасы деп аталады.

Функция графигін салу

Функциия графин салу үшін 1 А.О 2 жұп тақ периот 3 үзіліс нүктелерін 4 ассимптоталыр 5 функцияның 0-дері фунцияның таңба тұрақтылығы 6 экстремум нүктелері (өсу-кему аралығы) 7 иілу нүктесі (ойыс-дөңес таблца) 8 функцияның кейбір ерекшеліктері