Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский педагогический государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

сам.работа студентов по номеру зачетки.doc

Скачиваний:

Добавлен:

24.12.2018

Размер:

4.58 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

Функциональные ряды

Ряд

называется функциональным, если его члены являются функциями от х, т.е. , , которые определены на некотором множестве X.

Если переменной придавать различные числовые значения, то будут получаться сходящиеся или расходящиеся числовые ряды. Совокупность таких значений переменной х, при которых функциональный ряд сходится, называют областью сходимости. Областью сходимости ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.

По аналогии с числовыми рядами определяются частичные суммы функционального ряда, предел которых определяет сумму ряда (если существует). Очевидно, что сумма функционального ряда в области сходимости является функцией от х, т.е.

Говорят, что последовательность функций сходится равномерно к функции на множестве D, если для любого можно определить такой номер N, зависящий только от , что для любого и для всех выполняется неравенство

Ряд сходится равномерно на множестве D к сумме , если последовательность его частичных сумм сходится равномерно на множестве D к функции .

Приведем достаточный признак равномерной сходимости, который удобен в практическом применении.

Теорема (Признак Вейрштрассе). Если для членов функционального ряда выполняются неравенства

где , а – некоторые числа, не зависящие от х, и при этом числовой ряд сходится, то ряд сходится на множестве D равномерно.

Следующие теоремы устанавливают основные свойства равномерно сходящихся функциональных рядов.

Теорема. Если функции определены и непрерывны на множестве D, а ряд на этом же множестве сходится равномерно к сумме , то эта сумма будет непрерывной на D функцией.

Теорема. Если функции определены и непрерывны на множестве , а функциональный ряд на этом же множестве сходится равномерно к сумме , то его можно почленно интегрировать на , т.е.

Теорема. Пусть функции определены на и имеют непрерывные первые производные на . Если функциональный ряд сходится на отрезке , а функциональный ряд равномерно сходится на к сумме , то имеет на производную, причем

Заметим, что условия теорем достаточно жесткие, т.е. нельзя просто интегрировать и, особенно, дифференцировать функциональные ряды почленно. Это может привести к неверным результатам.

Степенным рядом называется функциональный ряд вида:

(123)

где – постоянные числа, называемые коэффициентами ряда.

Теорема (Абеля)

1) Если степенной ряд сходится при некотором значении , то абсолютно сходится при всяком значении , для которого справедливо .

2) Если степенной ряд расходится при некотором значении , то он расходится при всяком : .

Заметим, что теорема Абеля позволяет судить о расположении точек сходимости и расходимости степенного ряда. Действительно, если точка х0 – точка сходимости, то интервал заполнен точками абсолютной сходимости. Если – точка расходимости, то вся бесконечная полупрямая вправо от точки и вся полупрямая влево от точки – состоит из точек расходимости. Из этого можно заключить, что существует число R>0, что при мы имеем точки абсолютной сходимости, а при – точки расходимости. Интервалом сходимости степенного ряда называется такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится при том абсолютно, а для точек х, лежащих вне его, ряд расходится (рис. 22). Число R называется радиусом сходимости степенного ряда.

Рис. 22. Интервал сходимости степенного ряда

На концах интервала (т.е. при х = R, х = –R) вопрос о сходимости или расходимости остается не ясным. И для конкретного ряда решается индивидуально. Отметим, что у некоторых рядов интервал сходимости вырождается в точку R = 0, у других охватывает всю ось (R = ¥).

Теорема. Областью сходимости степенного ряда является интервал с центром в начале координат.

Укажем способ определения радиуса сходимости. Пусть имеем ряд (123). Рассмотрим ряд, составленный из абсолютных величин его членов:

(124)

Для определения сходимости ряда (124) применим признак Даламбера. Допустим, что существует предел:

Тогда по признаку Даламбера ряд (124) сходится, если <1, т.е. < и расходится, если , т.е. . Следовательно, ряд (123) сходится абсолютно при . Если же , то и ряд (124) расходится, при чем его общий член не стремится к нулю. Но тогда и общий член данного степенного ряда (123) не стремится к нулю, а это значит, на основании необходимого признака сходимости, что этот степенной ряд расходится (при ). Из предыдущего следует, что интервал есть интервал сходимости степенного ряда (123), т.е.

. (125)

Аналогично, по признаку Коши, можно определить интервал сходимости степенного ряда с радиусом

Пример 7.2.1. Определить интервал сходимости ряда

Решение. Применим для данного степенного ряда признак Даламбера:

Следовательно, ряд сходится при , так как предел не зависит от х. ►

Пример 2. Определить интервал сходимости ряда

Решение. Применим для данного степенного ряда признак Даламбера:

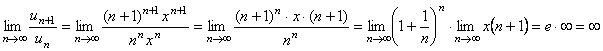
Таким образом, по формуле (125) радиус сходимости этого ряда равен нулю, поэтому ряд расходится при всех х, кроме х = 0. ►

Пример.3. Найти область сходимости степенного ряда .

Решение. Вычислим радиус сходимости ряда по формуле (125):

Таким образом, область сходимости данного степенного ряда . ►

Пример.4. Определить область сходимости ряда .

Решение. Так как для данного степенного ряда имеем , , то, применяя формулу для определения радиуса сходимости (125), получим:

Поскольку , то степенной ряд сходится в интервале (–1; 1). Чтобы решить вопрос о сходимости на концах интервала, исследуем на сходимость соответствующие числовые ряды. Полагая сначала , получаем – гармонический ряд, который расходится. При получаем ряд , который сходится по теореме Лейбница.

Таким образом, область сходимости степенного ряда есть полуинтервал [–1; 1). ►

Предположим, что функция , определена и раз дифференцируема в окрестности точки . Тогда она может быть представлена в виде ряда

, (126)

который называется рядом Маклорена.

Так же как и для числовых рядов, сумму ряда Маклорена можно представить в виде , где – -ая частичная сумма ряда; – -й остаток ряда.

Теорема. Для того чтобы ряд Маклорена сходился к функции , необходимо и достаточно, чтобы при остаток ряда стремился к нулю для всех из интервала сходимости ряда.