45. Непрерывность сложной функции. Непрерывность основных элементарных и принадлежащих классу элементарных функций.

Из приведенных выше теорем вытекает, что всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Т: Пусть функция u=φ(x) непрерывна в точке x0, а функция y=f(u) непрерывна в точке u0=φ(x0). Тогда сложная функция f(φ(x)), состоящая из непрерывных функций, непрерывна в точке x0.

Доказательство:

В силу непрерывности функции u=φ(x), 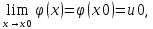то есть при x->x0 имеем u->u0. Поэтому вследствие непрерывности функции y=f(u) имеем:

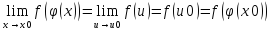
Это и доказывает, что сложная функция y=f(φ(x)) непрерывна в точке x0.

46. Сравнение и порядок бесконечно малых. Эквивалентные бесконечно малые и их свойства. Основные примеры эквивалентных бесконечно малых.

Две бмф сравниваются между собой с помошью их отношения.

Пусть α=α(x) и β=β(x) есть бмф при x->x0, т.е. 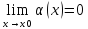и

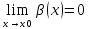
1) Если 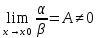то α и β называются бесконечно малыми одного порядка.

2) Если , то α – бесконечно малая более высокого порядка, чем β.

3) Если 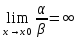, то α – бесконечно малая более низкого порядка, чем β.

4) Если 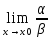– не существует, то α и β называются несравнимыми бесконечно малыми.

Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые.

Если , то α и β называются эквивалентными бесконечно малыми (при x->x0); это обозначается так: α ~ β.

Свойства:

1) Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.

Доказательство:

Пусть α ~ β при x->x0. Тогда

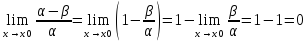
аналогично

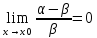
Справедливо и обратное утверждение: если разность бмф есть бесконечно малая высшего порядка, чем исходные, то они – эквивалентные бмф.

2)Сумма конечного числа бмф разных порядков эквивалентна слагаемому низшего порядка.

Доказательство:

Пусть α->0, β->0 при x->x0, причем α – бмф высшего порядка, чем β. Тогда

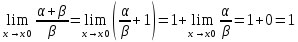
Следовательно, α+β ~ β при x->x0.

Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы.

Замена суммы бмф её главной частью называется отбрасыванием бм высшего порядка.

3)Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.

Доказательство:

Пусть α~α` и β~β` при x->x0. Тогда

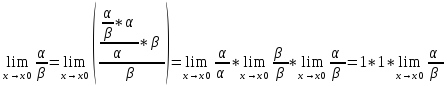
то есть

Основные примеры эквивалентных бесконечно малых:

1)

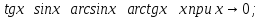
2)

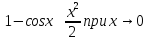
3)

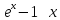
4)

5)

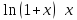
6)

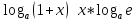
7)

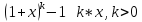
47.Сохранение знака непрерывности функции. Понятие равномерной непрерывности. Теорема Кантора (формулировка)

Пусть f(x) определена в окрестности точки x0 и непрерывна в точке x0, тогда в окрестности этой точки функция сохраняет свой знак и отделима от 0.

Отделимость от 0 на [a;b ] имеет место, если существует такое h, что для любого x 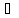[a;b ] следует, что |f(x)|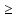 h >0.

Доказательство:

Считаем что f(x) >0. Пусть дано, что f(x) – непрерывна в точке x0.

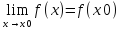Тогда тогда

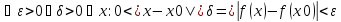
Возьмем ε = f(x0)/2, тогда

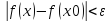
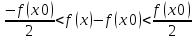
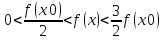
Равномерная непрерывность:

Условие:

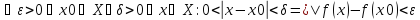
Теорема Кантора:

Если функция f(x)- непрерывна на отрезке [a,b], то она равномерно непрерывна на данном отрезке.