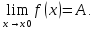37.Неограниченные величины. Бесконечно большие и их связь с бесконечно малыми.

Функция g(x) называется неограниченной в точке x0, если:

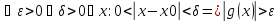
Функция g(x) называется бесконечно большой (частный случай неограниченной функции), если:

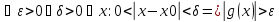
Связь бесконечно большой с бесконечно малой:

Пусть α(x) – бм. и не равна нулю в точке x0.

Для того, чтобы α(x) была бесконечно малой, необходимо, чтобы 1/ α(x) ,была бесконечно большой.

Необходимость:

Док-во: если α(x) – бм. то 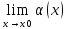=0 =>

1/α(x) > 1/ε

Пусть 1/ε =M>, тогда:

Следовательно 1/α(x) – бесконечно большая.

Достаточность доказывается аналогично.

38.Предел последовательности. Ограниченность последовательности, имеющей предел. Предел монотонной функции.

Под числовой последовательностью x1,x2,x3,…,xn понимается функция

xn=f(n),

заданная на множестве N натуральных чисел. Кратко последовательность обозначается в виде {xn} или xn, n 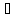N. Число x1 называется первым членом последовательности, xn – общим членом или n-м членом последовательности.

Последовательность {xn} называется ограниченной, если существует такое число M > 0, что для любого n N выполняется неравенство |xn| < = M

Предел последовательности:

Число a называется пределом последовательности {xn}, если для любого положительного ε найдется такое натуральное число N, что при всех n>N выполняется неравенство |xn-a|<ε

В этом случае пишут 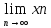==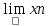 a или xn->a, и говорят, что последовательность {xn} имеет предел, равный числу a.

Коротко определение предела записывается так:

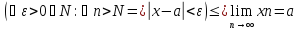
Ограниченность последовательности, имеющей предел:

Если последовательность имеет конечный предел, то она ограничена.

Док-во:

Дано 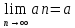. Запишем определение предела:

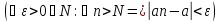
-ε<an-a< ε

a-ε<an<ε+a, но т.к. 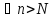– не выполняется для данного условия, введем новые переменные: m=min{m0;a-ε}; M=max{M0;a+ ε};

тогда m<=an<=M – последовательность ограничена.

Предел монотонной функции:

Признак существования предела монотонной функции: Если функция f(x) монотонна и ограничена при x<x0 или при x>x0, то существует соответственно её левый пред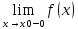ел = f(x-0) или её правый предел 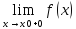=f(x0+0)

39.Предельный переход в равенствах и неравенствах. Теорема о «двух милиционерах».

Рассмотрим последовательности {xn}, {yn} и {zn}

Теорема: Если =a, 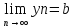и, начиная с некоторого номера, выполняется неравенство xn<=yn, то a<=b.

Доказательство:

Допустим, что a>b. Из равенств 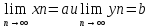следует, что для любого ε >0 найдется такое натуральное число N(ε), что при всех n>N(ε) будут выполняться неравенства |xn-a|<ε и |yn-b|<ε.

Т.е. a-ε < xn <a+ε и b-ε < yn < b+ε. Возьмем ε = (a-b)/2. Тогда xn>a-ε= a-(a-b)/2 = (a+b)/2

Также получаем, что yn<(a+b)/2 -> xn>yn . Это противоречит условию (xn<=yn). Следовательно a<=b

Теорема: Если 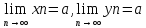и справедливо неравенство xn<=zn<=yn (начиная с некоторого номера), то

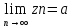
Примем без доказательств.

Теорема о пределе промежуточной функции:

Если функция f(x) заключена между двумя функциями g(x) и φ(x), стремящимися к одному и тому же пределу, то она также стремиться к этому пределу, т.е. если:

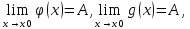
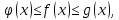
то

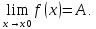
Доказательство:

Из равенств пределов вытекает, что для любого ε >0 существует две окрестности δ1 и δ2 точки x0, в одной из которых выполняется неравенство |φ(x) - A|<ε , т.е.

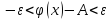
а в другой|g(x)-A| < 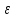, т.е.

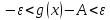
Пусть δ=min{δ1;δ2}. Тогда в δ-окрестности точки x0 выполняется оба неравенства.

В итоге получаем:

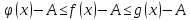
С учетом найденных нами неравенств мы получили что

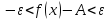
или

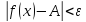
следовательно мы доказали, что