
- •33. Числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид:
- •34. Абсолютная величина и её свойства.
- •1)Аналитический.
- •2) Графический.
- •3) Табличный .
- •36.Предел функции и его единственность. Бесконечно малые и их свойства. Связь предела с бесконечно малыми.
- •37.Неограниченные величины. Бесконечно большие и их связь с бесконечно малыми.
- •38.Предел последовательности. Ограниченность последовательности, имеющей предел. Предел монотонной функции.
- •39.Предельный переход в равенствах и неравенствах. Теорема о «двух милиционерах».
- •40. Первый замечательный предел.
- •41. Второй замечательный предел.
- •42. Пределы, связанные со вторым замечательным.
- •43. Арифметические операции над переменными, имеющими предел. Неопределенные случаи.
- •44. Непрерывность функции в точке и на промежутке. Арифметические операции над непрерывными функциями. Условия непрерывности монотонной функции и существования для ней обратной непрерывности.
- •45. Непрерывность сложной функции. Непрерывность основных элементарных и принадлежащих классу элементарных функций.
- •46. Сравнение и порядок бесконечно малых. Эквивалентные бесконечно малые и их свойства. Основные примеры эквивалентных бесконечно малых.
- •47.Сохранение знака непрерывности функции. Понятие равномерной непрерывности. Теорема Кантора (формулировка)
- •48. Теоремы Больцано-Коши (с доказательством) и Вейерштрасса (формулировки) о свойствах непрерывных на отрезке функций.
40. Первый замечательный предел.
При вычислении
пределов выражений, содержащих
тригонометрические функции, часто
используют предел
 ,
,
называемый первым замечательным пределом. Читается так: предел отношения синуса к его аргументу равен единице, когда аргумент стремиться к нулю.
Доказательство:
Возьмем круг
радиуса 1, обозначив радианную меру угла
MOB через x.
Пусть 0 < x < π/2.
На рисунке |AM|=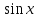 ,
дуга MB численно равна
центральному углу x, |BC|
= tgx. Очевидно, имеем
,
дуга MB численно равна
центральному углу x, |BC|
= tgx. Очевидно, имеем
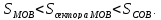 На основании соответствующих формул
геометрии получаем
На основании соответствующих формул
геометрии получаем
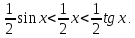 Разделим
неравенства на
Разделим
неравенства на
 ,
получим
,
получим
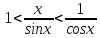 или
или
 .
Так как
.
Так как
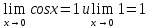 ,
то по признаку существования пределов
( о пределе промежуточной функции):
,
то по признаку существования пределов
( о пределе промежуточной функции):
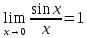
41. Второй замечательный предел.
Известно,
что предел числовой последовательности
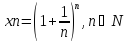 имеет предел, равный e.
имеет предел, равный e.
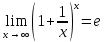
Данное равенство называется вторым замечательным пределом
42. Пределы, связанные со вторым замечательным.
1. Пусть
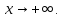 Каждое
значения x заключено между
двумя положительными целыми числами:
Каждое
значения x заключено между
двумя положительными целыми числами:
 ,
где n=[x] –
это целая часть x. Отсюда
следует
,
где n=[x] –
это целая часть x. Отсюда
следует
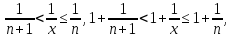 поэтому
поэтому

Если
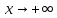 ,
то
,
то
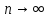 .
Поэтому имеем:
.
Поэтому имеем:
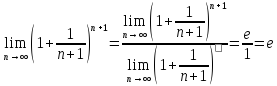
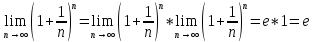
По признаку (о пределе промежуточной функции) существования пределов:
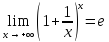
2. Пусть Сделаем подстановку –x=t,
тогда
Сделаем подстановку –x=t,
тогда
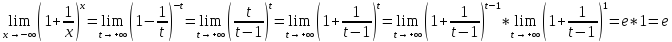
3. И если
произвести замену 1/x =a
(a->0 при x->∞),
то второй замечательный предел запишется
в виде


43. Арифметические операции над переменными, имеющими предел. Неопределенные случаи.
Переменными могут быть функции и последовательности (n->∞).
Пусть
существуют
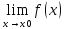 =a;
=a;
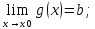
1)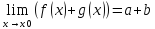 ;
;
2)
3)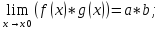
4)
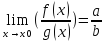 ;
;
Доказательство:
1) если
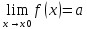 ,
то f(x)=a+α(x)
в точке x0;
,
то f(x)=a+α(x)
в точке x0;
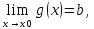 то g(x)=b+β(x),
где β(x),α(x)
– бесконечно малые.
то g(x)=b+β(x),
где β(x),α(x)
– бесконечно малые.
f(x)+g(x) = a+α(x)+b+ β(x) =a+b+β(x)+α(x), где β(x)+α(x)=γ(x) – бесконечно малая величина.
f(x)+g(x)=a+b+γ(x)
из этого следует, что
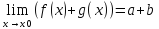 ;
;
3) если
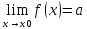 ,
то f(x)=a+α(x)
в точке x0;
,
то f(x)=a+α(x)
в точке x0;
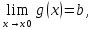 то g(x)=b+β(x),
где β(x),α(x)
– бесконечно малые.
то g(x)=b+β(x),
где β(x),α(x)
– бесконечно малые.
f(x)*g(x) =(a+α(x))*(b+ β(x))=a*b+a*α(x)+ b*α(x)+α(x)*β(x), где a*α(x)+ b*α(x)+α(x)*β(x)=γ(x) бесконечно малая величина.
f(x)*g(x)
= a*b +γ(x),
из чего следует, что
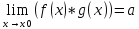 *b;
*b;
4) если
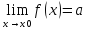 ,
то f(x)=a+α(x)
в точке x0;
,
то f(x)=a+α(x)
в точке x0;
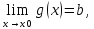 то g(x)=b+β(x),
где β(x),α(x)
– бесконечно малые.
то g(x)=b+β(x),
где β(x),α(x)
– бесконечно малые.
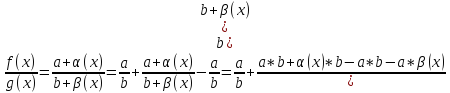 где
где
 =γ(x) – бесконечно малая
величина.
=γ(x) – бесконечно малая
величина.
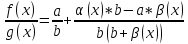 ,
что доказывает
,
что доказывает
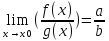
Рассмотрим случай, когда получается неопределенность вида [∞/∞]
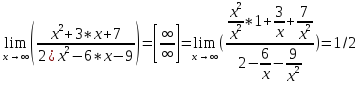
Вынесем из числителя и знаменателя x^2 и получаем, что неопределенность ушла, а остались только удобные числа. Так дроби у которых в знаменателе x стремятся к нулю, и получился ответ ½.
Таким образом при появлении неопределенности такого рода, необходимо выносить из числителя и знаменателя x в наибольшей степени, и подставлять в полученное выражение ∞.
Также если максимальные степени x в числителе и знаменателе не одинаковы, то ответ можно дать сразу, если в числителе степень больше, то предел равен бесконечности, а если в знаменателе – нулю
44. Непрерывность функции в точке и на промежутке. Арифметические операции над непрерывными функциями. Условия непрерывности монотонной функции и существования для ней обратной непрерывности.
Пусть
функция y=f(x)
определена в точке x0 и в
некоторой окрестности этой точки.
Функция y=f(x)
называется непрерывной в точке x0,
если существует предел функции в этой
точке и он равен значению функции в этой
точке, т.е.
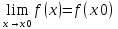
Данное равенство означает выполнение трех условий:
1) функция f(x) определена в точке x0 и её окрестности;
2) функция f(x) имеет предел при x->x0;
3) предел функции в точке x0 равен значению функции в этой точке, т.е. выполняется равенство выше.
Так как
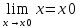 ,
то первое равенство можно записать так:
,
то первое равенство можно записать так:

Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функцию f(x) вместо аргумента x подставить его предельное значение x0.
Например,
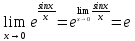 Предел и функция поменялись местами,
т.к. функция
Предел и функция поменялись местами,
т.к. функция
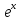 непрерывна.
непрерывна.
Также существует ещё одно определение непрерывной функции: y=f(x) называется непрерывной в точке x0, если она определена в точке x0 и её окрестности и выполняется равенство
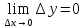
т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Функция непрерывна в интервале (a,b), если она непрерывна в каждой точке этого интервала.
Функция
непрерывна на отрезке [a,b],
если она непрерывна в интервале (a,b)
и в точке x=a
непрерывна справа (т.е.
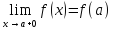 ),
а в точке x=b
непрерывна слева
(т.е.
),
а в точке x=b
непрерывна слева
(т.е.
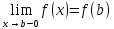 ).
).
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если x=x0 – точка разрыва функции y=f(x), то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции.
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Точкой
разрыва первого рода называется точка,
в которой существуют конечные пределы
функции слева и справа ( односторонние
пределы), т.е.
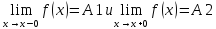
При этом:
а) если А1=А2, то точка x0 называется точкой устранимого разрыва.
б) если A1 ≠ A2, то точка x0 называется точкой конечного разрыва.
Величину |A1-A2| называют скачком функции в точке разрыва первого рода.
Точкой разрыва второго рода называется точка, в которой по крайней мере один из односторонних пределов не существует или равен бесконечности.
Основные теоремы о непрерывных функциях.
T1: Сумма, произведение и частное двух непрерывных функций есть функция непрерывная ( для частного за исключением тех значений аргумента, в которых делитель равен нулю).
Доказательство:
Пусть функция f(x) и φ(x) непрерывны на некотором множестве X и x0 – любое значение из этого множества. Докажем например непрерывность произведения F(x) = f(x)*φ(x). Применяя теорему о пределе произведения, получим:

Итак мы доказали непрерывность функции f(x)*φ(x) в точке x0.
T2: Если функция y=f(x) непрерывна и строго монотонна на [a,b] оси Ox, то обратная функция y=φ(x) также непрерывна и монотонна на соответствующем отрезке [c;d] оси Oy
Приводится без доказательств.
Из приведенных выше теорем вытекает, что всякая элементарная функция непрерывна в каждой точке, в которой она определена.
