Глава 5

Метод последовательного исключения Гаусса

5.1. Левообратимые бинарные операции

Пусть E =< E, ⊥> - алгебра с носителем E и семейством левообратимых бинарных операций ⊥ на E.

Определение. Бинарная на E операция ⊥ называется левообратимой, если уравнение

x ⊥ a = b

имеет решение x ∈ E, и притом единственное ∀ a, b ∈ E.

Согласно определению, левообратимая операция ⊥ имеет левообратимую обратную операцию

x = b a

такую, что выполнены тождества

(5.1)

(5.2)

(b ⊥ a) a = b

(b a) ⊥ a = b

∀a, b ∈ E

(5.3)

5.2. Двоякое понимание условия разрешимости

Условия существования и единственности уравнения (5.1) в реализованном аспекте могут пониматься двояко (в

узком и широком смыслах):

· как явная (формальная) разрешимость уравнения (5.1) относительно переменных

· как алгоритмическая (численная) разрешимость уравнения (5.1), то есть как существование алгоритма, который

по значениям a и b вычисляет значение переменной x, удовлетворяющее уравнению (5.1)

Очевидно, оба эти толкования разрешимости содержатся, как частные случаи, в более общем функциональном

толковании, то есть как функция y = x ⊥ a, биективно отображающая E на E для каждого значения "параметра"a ∈

E.

5.3. Пример левообратимой бинарной операции

Две последовательных цикловых (раундовых) фукнции шифра Фейстеля описываются следующим уравнением:

y1 = x1 ⊥ Φ(x2, k1)

y2 = x2 ⊥ Φ(x1 ⊥ Φ(x2, k1), k2)

или

y1 = x1 ⊥ Φ(x2, k1)

y2 = x2 ⊥ Φ(y1, k2)

Последнее преобразование можно понимать как новую левообратимую операцию ⊥ над E × E:

(y1, y2) = (x1, x2)⊥(k1, k2)

(x1, x2) = (y1, y2) ¯ (k1, k2)

или

y = xk

x = yk

(5.4)

(5.5)

(5.6)

(5.7)

(5.8)

(5.9)

(5.10)

(5.11)

:

5. Метод последовательного исключения Гаусса

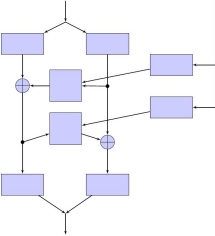
5.4. Пример левообратимой бинарной операции

X1

X

X2

K

K1

Φ

K2

Φ

Y1

Y

Y2

(y1, y2) = (x1, x2)(k1, k2)

(x1, x2) = (y1, y2)(k1, k2)

5.5. Последовательное исключение переменных

Определение. Независимая переменная системы уравнений

(5.12)

(5.13)

F :

yi = fi(x1, x2, . . . , xn)

1 ≤ i ≤ n

(5.14)

называется ведущей относительно остальных переменных, если:

· во-первых, система () имеет в своем составе хотя бы одно уравнение, явно разрешимое относительно указанной

перменной

· во-вторых, редуцированная система, полученная исключением указанной переменной из остальных уравнений

системы (), вновь имеет в своем составе хотя бы одно уравнение, явно разрешимое относительно некоторой из

своих независимых переменных

Утверждение. Система F допускает последовательное исключение переменных тогда и только тогда, когда она

характеризуется некоторым порядком ее независимых переменных, в котором каждая переменная оказывается веду-

щей относительно всех последующих.

Определение. Систему F будем называть гауссовой, если она допускает последовательное исключение перемен-

ных. Гауссову систему F , допускающую последовательное исключение переменных в порядке x1, x2, . . . , xn будем

называть номинальной.

Утверждение. Всякая гауссова система элементарными преобразованиями может быть приведена к номинальной

форме.

Утверждение. Номинальная система F , отображающая E1 × E2 × . . . × En на себя, процедурой последовательного

исключения переменных преобразуется к равносильной системе G:

G :

yi = gi(y1, . . . , yi−1, xi, xi+1, . . . , xn)

1 ≤ i ≤ n

(5.15)

где каждое i-е уравнение явно разрешимо относительно i-й переменной xi, при этом рекурсивно порождается отобра-

жение

18

5.6. Последовательное исключение переменных

G−1 :

−1

yi = gi (y1, . . . , yi−1, xi, xi+1, . . . , xn)

1 ≤ i ≤ n

(5.16)

где каждое i-е уравнение явно разрешимо относительно i-й переменной и система G−1 является обращением системы

G.

5.6. Последовательное исключение переменных

В результате последовательного исключения переменных из номинальной системы F синхронно (пошагово) гене-

рируются две системы G и G−1:

G :



 y1 = g1(x1, x2, x3, . . . , xn)



 y2 = g2(x1, x2, x3, . . . , xn)



y = g3(x1, x2, x3, . . . , xn)

 ...



 yn = gn(x1, x2, x3, . . . , xn)

(5.17)

G :

−1

 x1 = gn (y1, y2, y3, . . . , yn)

 x2 = gn−1(y1, y2, y3, . . . , yn)

−1

x3 = gn−2(y1, y2, y3, . . . , yn) .

(5.18)



 ...

 xn = g−1(y1, y2, y3, . . . , yn)

Система G равнозначна исходной системе F . При этом каждое i-е уравнение системы G явно разрешимо относи-

тельно i-й переменной, благодаря чему возникает вторая система G−1.

Определение. Системы вида G и G−1, в которых каждое i-е уравнение является биективной функцией по i-й

переменной при любых допустимых значениях других переменных, будем называть g-треугольными (соответственно

номинальной и кономинальной) порядка n × n.

5.7. Выводы по методу последовательного исключения переменных

1. Любая гауссова система F , то есть система, допускающая последовательное исключение переменных, переста-

новкой уравнений и соответствующим преобозначением переменных, может быть преобразована к номинальной

форме.

2. Любая номинальная гауссова система F равнозначна номинальной g-треугольной системе; обращением g-треугольной

номинальной системы служит кономинальная g-треугольная система.

3. Понятие g-треугольных систем не требует (хотя и не исключает) выполнения условий явной разрешимости их

относительно соответствующих независимых переменных. Тем самым понятие g-треугольных систем обобщает

понятие гауссовых систем.

5.8. Метод Гаусса-Зейделя

Дана система F . Требуется найти неподвижную точку отображения F , то есть решить систему уравнений:



x1 = f1(x1, x2, . . . , xn)

x2 = f2(x1, x2, . . . , xn)

. . .



xn = fn(x1, x2, . . . , xn)

(5.19)

В вычислительной математике широко распространены два метода итераций - метод простой итерации и метод

Гаусса-Зейделя.

· Решение системы методом простой итерации. Задается начальное приближение (x0, x0, . . . , xn). Последующие

приближения строятся согласно итерациям:



= fi(xk , xk , . . . , xn)

1 ≤ i ≤ n

(5.20)



k = 0, 1, 2, . . .

· Решение системы методом Гаусса-Зейделя. При тех же начальных данных последующие приближения строятся

согласно итерациям:

19







 3







−1





























01 2

 (k+1)

xi

k1 2



5. Метод последовательного исключения Гаусса

 (k+1) (k+1)

xi = fi(x1

1 ≤ i ≤ n

(k+1)

, . . . , xi−1 , xk , xi+1, . . . , xn)

(5.21)

k = 0, 1, 2, . . .

Метод итераций Гаусса-Зейделя алгоритмически равнозначен методу простой итерации:



x1 = f1(x1, x2, . . . , xn)



F : x2 = f2(x1, x2, . . . , xn)

. . .



xn = fn(x1, x2, . . . , xn)

(5.22)

Определение. Пусть задана последовательность g-треугольных систем G1, G2, . . . , Gt, отображающих E1 × E2 ×

. . . × En на себя. Композицию этих отображений

GZi := Gt ◦ Gt−1 ◦ . . . ◦ G2 ◦ G1

(5.23)

будем называть отображением Гаусса-Зейделя ранга t, t ∈ N

Если Gi = G ∀t, то GZi = Gt, и, трактуя параметр t как дискретное время, последовательность x0, x1, . . . , xi, . . .,

где xt = Gt(x0), обычно понимается как траектория системы G.

Вывод: GZ-отображения, построенные на базе g-треугольных систем расширяют класс обратимых отображений

на E1 × E2 × . . . × En.

5.9. G-треугольные системы как левообратимые бинарные операци на

декартовом произведении множеств

Пусть задано произвольное отображение F множества E1 × E2 × . . . × En на себя:

F :

yi = fi(x1, x2, . . . , xn)

1 ≤ i ≤ n

(5.24)

и пусть на каждом множестве Ei(1 ≤ i ≤ n) определена левообратимая бинарная операция ⊥i, пусть, далее, (a1, a2, . . . , an)

- произвольный элемент декартового произведения E1 × E2 × . . . × En. Образуем новую систему:

G :

yi = xi ⊥i fi(y1, . . . , yi−1, ai, xi+1, . . . , xn)

1 ≤ i ≤ n

(5.25)

Очевидно, эта система g-треугольна. Синтезированную на базе произвольной системы F g-треугольную систему G

можно рассматривать на E1 × E2 × . . . × En как левообратимую бинарную операцию ⊥F в базисе F :

¯ = x⊥F a

(5.26)

Отметим, что при E1 = E2 = . . . = En = E, пересталяя уравнения системы F, а также используя бинарные

операции {⊥i}i=1 в различных порядках, можно получить (n!)3, вообще говоря, различных g-треугольных систем

(бинарных операций на E n).

5.10. Применение G-треугольных систем в криптографии

G-треугольные системы обобщают сети Фейстеля

Форма 1 сбалансированной системы

...

z1 = y1 ⊥1 ϕ1(t1, . . . , tn) = x1 ⊥2 f1(k1, x2, . . . , xn)

z2 = y2 ⊥1 ϕ2(y1, t2, . . . , tn) = x2 ⊥2 f2(y1, k2, x3, . . . , xn)

z3 = y3 ⊥1 ϕ3(y1, y2, t3, . . . , tn) = x3 ⊥2 f3(y1, y2, k3, x4, . . . , xn)

(5.27)

(5.30)

zn = yn ⊥1 ϕn(y1, y2, . . . , yn−1, tn) = xn ⊥2 fn(k1, x2, . . . , xn)

Сбалансированная система биективно отображает E n на E n. Здесь: (x1, x2, . . . , xn) - входные переменные; (z1, z2, . . . , zn)

- выходные переменные; (t1, t2, . . . , tn) - свободные переменные (т.е. параметры).

Алгоритм прямого преобразования (первая форма)

Вход

1 шаг

(x1, x2, . . . , xn)

(t1, t2, . . . , tn)

Выход (z1, z2, . . . , zn)

20



ki k











˜

y ¯ ¯

n

(5.28)

(5.29)

(5.31)

5.10. Применение G-треугольных систем в криптографии

z1 = x1 ⊥2 f1(k1, x2, . . . , xn){на выход}

y1 = z1 1ϕ1(t1, t2, . . . , tn){промежуточное состояние}

2 шаг

z2 = x2 ⊥2 f2(y1, k2, x3, . . . , xn){на выход}

y2 = z2 1ϕ2(y1, t2, . . . , tn){промежуточное состояние}

...

n-й шаг

zn = xn ⊥2 fn(y1, . . . , yn−1, kn){на выход

Алгоритм обратного преобразования (первая форма)

Вход

(z1, z2, . . . , zn)

(t1, t2, . . . , tn)

Выход (x1, x2, . . . , xn)

1 этап

Вход: (z1, z2, . . . , zn); (t1, t2, . . . , tn) - параметр

Выход: (y1, y2, . . . , yn−1)

1 шаг y1 = z1 1ϕ1(t1, t2, . . . , tn)

2 шаг y2 = z2 2ϕ1(y1, t2, . . . , tn)

...

n-й шаг yn = zn 1ϕn(y1, . . . , yn−1, tn)

2 этап

Вход: (z1, z2, . . . , zn); (y1, y2, . . . , yn)

Выход: (x1, x2, . . . , xn)

1 шаг xn = zn 2fn(y1, y2, . . . , yn−1, kn) { на выход }

2 шаг xn−1 = zn−1 2fn−1(y1, y2, . . . , yn−2, kn−1, xn) { на выход }

...

(n-1)-й шаг x2 = z2 2f2(y1, k2, x3, . . . , xn) { на выход }

n-й шаг x1 = z1 2f1(k1, x2, . . . , xn) { на выход }

Все входные состояния не хранятся после декодирования.

Форма 2 сбалансированной системы

z1 = y1 ⊥1 ϕ1(t1, . . . , tn) = x1 ⊥2 f1(k1, x2, . . . , xn)

z2 = y2 ⊥1 ϕ2(y1, t2, . . . , tn) = x2 ⊥2 f2(y1, k2, x3, . . . , xn)

z3 = y3 ⊥1 ϕ3(y1, y2, t3, . . . , tn) = x3 ⊥2 f3(y1, y2, k3, x4, . . . , xn)

...

zn = yn ⊥1 ϕn(y1, y2, . . . , yn−1, tn) = xn ⊥2 fn(k1, x2, . . . , xn)

Здесь те же входные, выходные и свободные переменные, что и в форме 1.

Алгоритм прямого преобразования (вторая форма)

(5.32)

(5.35)

Вход

(x1, x2, . . . , xn)

(t1, t2, . . . , tn)

Выход (z1, z2, . . . , zn)

1 шаг

z1 = x1 ⊥2 f1(k1, x2, . . . , xn){на выход}

y1 = z1 1ϕ1(t1, t2, . . . , tn){промежуточное состояние}

2 шаг

z2 = x2 ⊥2 f2(y1, k2, x3, . . . , xn){на выход}

y2 = z2 1ϕ2(y1, t2, . . . , tn){промежуточное состояние}

...

n-й шаг

zn = x2 ⊥2 fn(y1, . . . , yn−1, kn){на выход

Алгоритм обратного преобразования (вторая форма)

Вход

(z1, z2, . . . , zn)

(t1, t2, . . . , tn)

Выход (x1, x2, . . . , xn)

1 этап

Вход: (z1, z2, . . . , zn); (t1, t2, . . . , tn) - параметр

Выход: (y1, y2, . . . , yn−1)

1 шаг y1 = z1 1ϕ1(t1, t2, . . . , tn)

2 шаг y2 = z2 2ϕ1(y1, t2, . . . , tn)

...

n-й шаг yn = zn 1ϕn(y1, . . . , yn−1, tn)

2 этап

Вход: (z1, z2, . . . , zn); (y1, y2, . . . , yn)

Выход: (x1, x2, . . . , xn)

21

(5.33)

(5.34)

(5.36)

5. Метод последовательного исключения Гаусса

1 шаг xn = zn 2fn(y1, y2, . . . , yn−1, kn) { на выход }

2 шаг xn−1 = zn−1 2fn−1(y1, y2, . . . , yn−2, kn−1, xn) { на выход }

...

(n-1)-й шаг x2 = z2 2f2(y1, k2, x3, . . . , xn) { на выход }

n-й шаг x1 = z1 2f1(k1, x2, . . . , xn) { на выход }

22