
DEGTYREV
.pdf
Министерство образования и науки Российской Федерации
Московский государственный институт электронной техники (технический университет)
В.З. Гребенкин, А.А. Дегтярев, В.А. Летягин
Метрология
Лабораторный практикум
Под редакцией доцента А.А. Дегтярева
Утверждено редакционно-издательским советом института
Москва 2010
PDF created with pdfFactory Pro trial version www.pdffactory.com
УДК 006.91
Рецензент канд. техн. наук, доц. А.П. Кожевников
Гребенкин В.З., Дегтярев А.А., Летягин В.А.
Метрология: Лабораторный практикум / Под ред. А.А. Дегтярева. - М.: МИЭТ, 2010. - 124 с.: ил.
В лабораторный практикум включены описания работ, содержание которых отражает некоторые аспекты деятельности по обеспечению единства измерений. Описание каждой работы содержит необходимые теоретические сведения, справочные материалы, схемы и описание средств измерений, методики выполнения работ, требования к оформлению отчетов и контрольные вопросы.
Для студентов инженерных направлений подготовки и специальностей, изучающих учебную дисциплину "Метрология, стандартизация и подтверждение соответствия".
ã МИЭТ, 2010
PDF created with pdfFactory Pro trial version www.pdffactory.com
Лабораторный практикум
Гребенкин Владимир Захарович Дегтярев Александр Анатольевич Летягин Валерий Афанасьевич
Метрология
Редактор Е.Г. Кузнецова. Технический редактор Л.Г. Лосякова. Корректор Л.Г. Лосякова. Верстка авторов.
Подписано в печать с оригинал-макета 22.09.2010. Формат 60х84 1/16. Печать офсетная. Бумага офсетная. Гарнитура Times New Roman. Усл. печ. л. 7,19. Уч.-изд. л. 6,2. Тираж 350 экз. Заказ 88.
Отпечатано в типографии ИПК МИЭТ.
124498, Москва, Зеленоград, проезд 4806, д. 5, МИЭТ.
PDF created with pdfFactory Pro trial version www.pdffactory.com
Практическая часть
Лабораторная работа № 1. Статистический контроль партии деталей
Цель работы: изучение основных характеристик точности партии деталей; ознакомление с методами статистической обработки результатов наблюдений; приобретение навыков массовых измерений и статистического анализа массива данных.
Продолжительность работы: 2 или 4 часа.
Оборудование и средства измерительной техники: набор плоскопараллельных концевых мер длины,
измерительная головка, поверочная плита, стойка или штатив.
Теоретические сведения
Обработка результатов наблюдений широко применяется в производственной практике для установления соответствия выбранного оборудования и технологического процесса заданной точности параметров изделия, определения статистических характеристик партии деталей, оценки точности методов и средств измерений и т.д.
Согласно ГОСТ 15895-77 точность технологического процесса - свойство, обусловливающее близость значений действительных и номинальных параметров продукции (в частности, ее размеров). Точность технологического процесса и закономерности его протекания во времени оцениваются рядом показателей, которые составляют предмет статистического анализа. Применительно к геометрическим параметрам это прежде всего характер их рассеяния, представляемый графически кривой распределения, которая определяется экспериментально. Для получения такой кривой рекомендуется выполнить порядка 100 наблюдений фактических значений исследуемого параметра.
При изготовлении конкретной детали каждый ее размер отклоняется от заданного чертежом значения ввиду погрешностей в системе станок - приспособление - инструмент - деталь (СПИД): износа элементов станка и режущего инструмента, вибраций инструмента и детали вследствие непостоянства твердости и структуры материала детали, изменения температуры инструмента и детали в процессе ее обработки, а также многих других факторов. Поэтому для партии деталей характерен неизбежный разброс (рассеяние) их размеров. Результат однократного измерения размера конкретной детали (результат наблюдения) является случайной величиной. Теоретически предсказать параметры рассеяния невозможно: для этого необходимо знать и учитывать физическую природу всех факторов, влияющих на точность обработки. Вследствие этого для обработки результатов измерений используют методы теории вероятностей и математической статистики, позволяющие рассчитать статистические параметры эмпирического распределения, а также установить параметры теоретического распределения, которое в наибольшей степени соответствует исследуемому эмпирическому распределению.
Появление того или иного числового значения величины в результате массовых измерений рассматривается как случайное событие. Характеризуется оно только тем, что оно возможно. Отношение числа п случаев появления события А к числу N произведенных испытаний, при которых это событие могло появиться, называется относительной частотой (частостью) события А:
W(A) = n / N.
PDF created with pdfFactory Pro trial version www.pdffactory.com
При увеличении числа испытаний N частость события A становится устойчивой, и значение W(A) колеблется около некоторого постоянного числа. Это число, меньшее единицы, называется вероятностью P(A) появления события A. За приближенное значение вероятности P(A) появления события A при достаточно большом числе испытаний можно принять частость W(A):
P(A) @ W(A) = n / N.
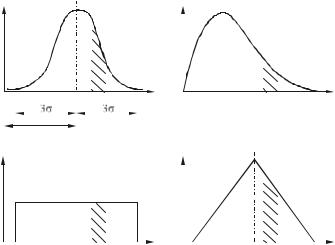
Зависимость между числовым значением х непрерывной случайной величины и вероятностью P(х) его появления устанавливается законом распределения вероятностей случайных величин. Наиболее часто используются следующие виды законов распределения отклонений параметров изделий: нормального распределения, эксцентриситета, равной вероятности, треугольника (рис.1).
y |
y |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x1 |
x2 |
x |
x1 |
x2 |
x |
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
a |
|
а |
|
|
|
б |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
y |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
y |
|
|
|
|||
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
x1 |
x2 |
x |
x1 |
x2 |
x |
|||||||
|
|
|||||||||||
|
в |
|
|
|
|
г |
|
|
|
|||
Рис.1. Кривые распределения отклонений для законов: а - нормального распределения; б - эксцентриситета; в - равной вероятности; г - треугольника
Закон нормального распределения (закон Гаусса) характеризуется тем, что ни один из внешних факторов, влияющих на величины и знаки отклонений, не является доминирующим, а отклонения параметра могут принимать как положительные, так и отрицательные значения.
Закон эксцентриситета (законы Максвелла, Рэлея) реализуется в тех случаях, когда отклонения параметра - величины существенно положительные (Dxi ³ 0).
Закон равной вероятности (закон прямоугольника) характерен для ситуации, когда доминирующий фактор вызывает монотонное изменение параметра с течением времени.
Закон треугольника (закон Симпсона) реализуется при суммировании двух независимых случайных величин, распределение значений которых подчиняется закону равной вероятности; он используется также для приближенного описания более сложных законов распределения.
Закон нормального распределения рассмотрим подробнее. Этому закону с некоторым приближением может подчиняться рассеяние погрешностей изготовления или измерения линейных и угловых размеров, погрешностей массы деталей, механических и физических величин, характеризующих свойства материалов.
PDF created with pdfFactory Pro trial version www.pdffactory.com

Кривая, изображающая плотность распределения для этого закона (см. рис.1,а), определяется
уравнением (функцией распределения) |
|
|
|
|
|
|
|
|
y = |
1 |
|
çæ |
|
(x - a)2 |
÷ö |
||
|
|
|
|
|
|
|||
σ 2π |
|
×expç |
- |
2σ |
2 |
÷, |
||
|
è |
|
|
ø |
||||
где у - плотность распределения вероятности случайной величины; а и s - параметры распределения.
Величина параметра а равна математическому ожиданию М(х) дискретной случайной величины x:
M(x) = Sxi×P(xi),
где хi - возможное значение случайной величины; P(хi) - вероятность появления значения хi случайной величины.
Значение М(х) характеризует положение центра группирования случайных величин, около которого располагаются, например, действительные значения данного параметра. При отсутствии систематических погрешностей результатов многократных измерений одной и той же величины в одних и тех же условиях математическое ожидание в наибольшей степени приближается к истинному значению измеряемой величины, т.е. к значению, свободному от ошибок измерения. При анализе характера рассеяния размеров деталей, обрабатываемых на станке, математическое ожидание можно рассматривать как размер, на который был настроен станок.
Параметр σ характеризует степень рассеяния значений случайной величины относительно центра группирования. Его называют средним квадратичным отклонением случайной величины и определяют по формуле
s = 
 å[xi - M (x)]2 × P(xi ).
å[xi - M (x)]2 × P(xi ).
Ветви теоретической кривой нормального распределения уходят в бесконечность, асимптотически приближаясь к оси абсцисс. Площадь, ограниченная кривой и осью абсцисс, равна вероятности того, что случайная величина лежит в интервале от -∞ до +∞. Ее принимают равной 1 (единице) или 100%.
Площади, ограниченные отрезками [x1x2], кривыми графиков плотности вероятности и ординатами, соответствующими границам отрезков х1 и х2, представляют собой вероятности попадания случайной величины xi в данные интервалы (на рис.1 эти площади заштрихованы). При распределении случайной величины по закону Гаусса поле шириной R = 6s принимают за практически предельное поле рассеяния случайной величины (вероятность выхода за его пределы составляет менее 0,27%).
Статистический приемочный контроль качества продукции применяют в тех случаях, когда проведение сплошного контроля осуществить трудно из-за большого массива партии изделий или даже невозможно (например, когда проведение контроля связано с разрушением изделия). Подобный вид контроля называют выборочным.
Из общего числа изготовленных деталей периодически делают выборки объемом Ni деталей и производят измерение наиболее ответственного размера d на всех деталях каждой выборки с целью анализа
PDF created with pdfFactory Pro trial version www.pdffactory.com
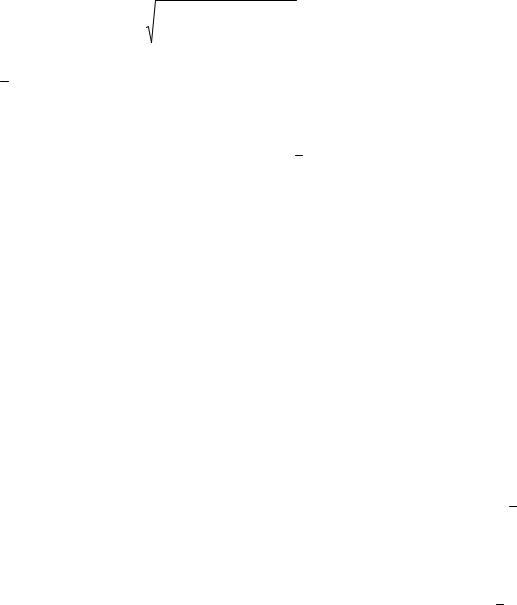
правильности выбора технологического процесса по критерию точности обработки этого размера. Диапазон действительных значений размера d разбивают на k равных по ширине интервалов, строят гистограмму и полигон распределения, а также определяют основные статистические характеристики эмпирического распределения:
∙ среднее арифметическое действительных размеров выборки
|
|
= ådi / N; |
|
d |
(1) |
||
∙ стандартное отклонение (в отечественной практике часто используется термин "среднее квадратичное отклонение")
|
1 |
|
k |
|
|||
S = |
|
×å((di - |
|
)2 × ni ) . |
(2) |
||
|
d |
||||||
N -1 |
|||||||
|
i=1 |
|
|||||
|
|
|
|
||||
Параметры d и S, определенные по данным выборки с ограниченным числом наблюдений, дают лишь приблизительную характеристику теоретического распределения.
Между параметрами теоретического распределения (математическим ожиданием М(х) и средним квадратичным отклонением σ) и их эмпирическими аналогами d и S необходимо проводить четкое разграничение: первые рассматриваются как постоянные, но неизвестные величины, характеризующие теоретическое распределение, а вторые являются случайными величинами и, будучи определенными из выборочных наблюдений, дают лишь приблизительную оценку M(х) и σ.
Диапазон рассеяния отклонений для партии деталей при нормальном законе распределения принимают равным
R = 6S. |
(3) |
Отношение допуска T размера, заданного чертежом, к диапазону рассеяния R называют
коэффициентом точности технологического процесса Tп. Если R больше T (т.е. Tп < 1), следует существенно изменить технологический процесс: использовать более точный станок, более стойкий инструмент, стабилизировать температуру детали и помещения и т.д. Если R меньше T (т.е. Tп > 1), технологический процесс соответствует требованиям к точности контролируемого параметра.
Однако поле рассеяния может быть смещено относительно заданного поля допуска (рис.2). В таком
случае требуется коррекция технологического процесса. Разность между средним арифметическим d ,
характеризующим положение центра группирования действительных отклонений, и средним значением размера dm = d + ec определяет необходимую величину коррекции технологического процесса: настройку станка или замену размерного инструмента. Отношение разности к допуску Т называют коэффициентом смещения Е.
Коэффициент Е показывает в относительных единицах, насколько фактическое среднее арифметическое d не совпадает с заданным средним значением размера dm.
PDF created with pdfFactory Pro trial version www.pdffactory.com
|
|
|
|
T |
|
|
|
ei |
Поле допуска |
|
|
|
|
d |
ec d |
es d |
|
ni |
d |
|
min |
m |
max |
|
|
0,5T |
|
||
7 |
|
|
|
|
|
6 |
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
5 |
|
1 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
НГ |
|
|
ВГ |
0 |
d |
1 2 3 4 5 6 7 |
8 9 10111213141516 d |
||
|
|
|
3S |
3S |
|
|
|
|
Поле рассеяния |
|
|
|
|
|
R |
|
|
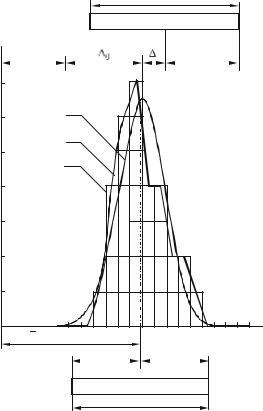
Рис.2. Графическое представление распределения отклонений: 1 - гистограмма; 2 - полигон распределения; 3 - теоретическая кривая распределения
Для идеально настроенного технологического процесса Тп = 1 и Е = 0.
Теоретический закон распределения вероятностей предполагает непрерывность случайной величины и обычно выражается в форме функции распределения или ее графика (см. рис.1). При статистической обработке массива результатов измерений с ограниченным объемом выборки оперируют с дискретной случайной величиной, принимающей значения середин интервалов, на которые разбит диапазон действительных значений размера. В этом случае закономерность распределения относительной частоты (частости) случайной величины представляют в форме графика - гистограммы, состоящей из прямоугольников, или эмпирической кривой распределения (которую называют также полигоном), или в форме таблицы.
После построения гистограммы или полигона подбирается теоретическая кривая распределения, которая, выражая существенные черты эмпирического распределения, сглаживает все случайности, связанные с недостаточным объемом экспериментальных данных.
Вертикальная координата теоретической кривой распределения вычисляется по формулам:
nTi = (N∙Δd∙f(zi))/S - для закона нормального распределения; |
(4) |
||
|
|
|
|
nTi = N∙Δd(1 - ½d0i - d |
½/3S)/3S - для закона Симпсона; |
(5) |
|
nTi = (N∙Δd) /6S - для закона равной вероятности. |
(6) |
||
PDF created with pdfFactory Pro trial version www.pdffactory.com
Здесь N - размер исследуемой выборки (суммарное число изделий); d = dmax i - ширина интервала размеров; S - стандартное отклонение; f(zi) - значение дифференциальной функции Лапласа (табл.1); zi = |d0i
– d |/S - относительная координата.
На рис.2 представлены гистограмма, полигон распределения, теоретическая кривая распределения (соответствующая закону Гаусса) для одной и той же экспериментальной выборки.
Графически вероятность получения годных изделий оценивается долей площади под кривой теоретического распределения, соответствующей заданному полю допуска. По результатам статистической обработки партии деталей может быть вычислена вероятность брака.
|
es |
|
x1 |
T |
ec |
|
R |
|
x2 |
|
ei |
0 + |
|
d |
d |
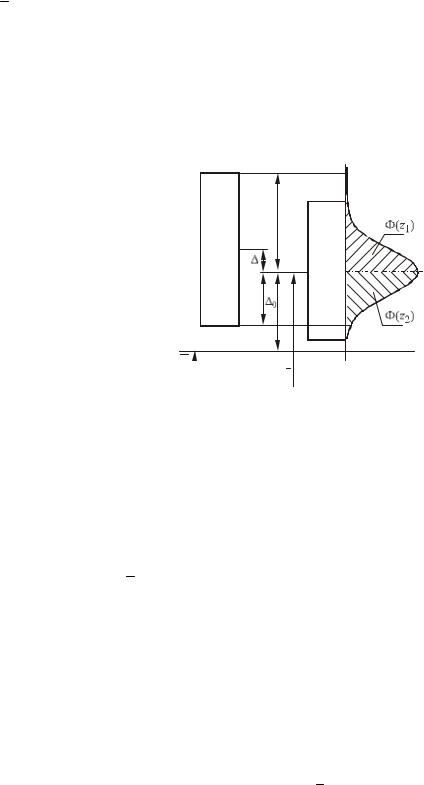
Рис.3. Схема для вычисления процента годных деталей |
|
Для закона нормального распределения (рис.3) вероятность брака рассчитывается по зависимости
Pбр = 1 – (Ф(z1) + Ф(z2)). |
(7) |
Здесь Ф(zi) - значение интегральной функции Лапласа (табл.2); zi = xi/S - относительная (нормированная)
координата; x1 = çes - D0ç и x2 = çei - D0ç - координаты границ заданного поля допуска относительно центра
группирования D0 = d – d .
Для других законов распределения в случае выхода поля рассеяния за одну границу заданного поля
допуска вероятность брака рассчитывается по одной из формул: |
|
Pбр = (3S – l)2/18S2 - для закона Симпсона; |
(8) |
Pбр = (3S – l)/6S - для закона равной вероятности. |
(9) |
Здесь l - длина интервала от центра группирования d до соответствующей границы заданного поля допуска; l < 3S.
При большом числе наблюдений (N > 50) проводится проверка соответствия выбранного теоретического закона эмпирическому распределению. Проверка проводится на основе критерия согласия Пирсона (критерия c2). При этом используются результаты измерений и вычислений, выполненных в данной работе: ni - реальное
PDF created with pdfFactory Pro trial version www.pdffactory.com
число изделий в интервале (частота) и nTi - теоретическое число изделий в том же интервале.
Если в каком-либо интервале ni < 4, то данный интервал в обоих распределениях (эмпирическом и теоретическом) объединяется с соседним интервалом. Далее определяется число степеней свободы v = K – 3, где K - общее число интервалов после укрупнения. Вычисляется показатель относительной разности частот
χ2 = ∑ χ2i , где χ2i = (nТi – ni)2 / nТi.
Назначается уровень значимости q, для которого рекомендуется выбирать значения от 2 до 10%.
Применяется двусторонняя критическая область, т.е. оценивается вероятность Р { χ12 ≤ χ2 ≤ χ22 } = q. По табл.3
определяется значение χ12 для числа степеней свободы ν и уровня значимости q1 = 0,5q и значение χ22 для того же ν и уровня значимости q2 = 100 – q1. Гипотеза о соответствии выбранного вида теоретического закона реальному распределению отклонений в проверяемой выборке принимается, если выполняется условие
χ12 ≤ χ2 ≤ χ22 .
Средства измерений
В зависимости от заданной точности контролируемого размера выбирается конкретный вид измерительной головки. Измерительные головки (зубчатые, рычажно-зубчатые, пружинные, пружинно-оптические) предназначены для измерений линейных размеров (как правило, дифференциальным методом), отклонений формы и расположения поверхностей.
Индикатор часового типа является зубчатой измерительной головкой. Выпускаются два типа индикаторов: радиальный ИЧ (с перемещением измерительного стержня параллельно плоскости шкалы) и торцовый ИТ (с перемещением стержня перпендикулярно плоскости шкалы).
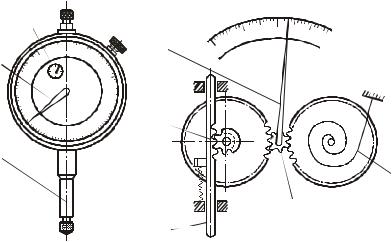
Внешний вид и схема индикатора ИЧ представлены на рис.4.
9
6 |
|
0 |
90 |
10 |
|
|
80 |
20 |
|
70 |
30 |
|
60 |
40 |
|
50 |
|
|
|
1
90 0 10
6 80
3
2
10 |
7 |
|
8 |
||
4 |
||
5 |
||
1 |
|
а |
б |
Рис.4. Индикатор часового типа: а - внешний вид; б - схема. 1 - измерительный стержень; 2 - зубчатая рейка; 3, 4, 5, 8 - зубчатые колеса; 6 - основная стрелка; 7 - спиральная пружина (волосок); 9 - стрелка указателя оборотов; 10 - пружина
Возвратно-поступательное перемещение измерительного стержня 1 с нарезанной зубчатой рейкой 2 через зубчатые колеса 3, 4 и 5 преобразуется в круговое движение стрелки 6. Спиральная пружина (волосок) 7, воздействуя на зубчатое колесо 8, устраняет зазоры во всех зацеплениях. На оси зубчатого колеса 3 насажена стрелка 9 указателя оборотов основной стрелки 6. Измерительное усилие создается пружиной 10.
PDF created with pdfFactory Pro trial version www.pdffactory.com
