18. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели множественной регрессии.

Основная спецификация математической модели: Yt = a₀ +a₁X_1t +...+a_kX_kt +ἐ_t

X_1t... X_kt - экзогенная независимая переменная, Yt - эндогенная зависимая переменная, a_0... a_k - неизвестные коэффициенты регрессии, подлежащие оценки, ἐ_t - последовательность случайных величин, удовлетворяющие условиям теоремы Гаусса-Маркова. _, ; ; ;

Y^= XA=*;

В соответствии с МНК найдем minESS: min(поА) (Y-XA)^T(Y-XA)=min(Y^TY-2A^TX^TY+A^TX^TXA), = -2X^TY+2X^TXA=0. Откуда получим систему нормальных уравнений: X^TXA= X^TY, то A = (X*X^T)^-1X^TY

19. Модель парной регрессии. Границы доверительных интервалов.

Наша задача – подобрать функцию так, чтобы она проходила на наименьшем расстоянии от всех точек сразу. Для этого необходимо минимизировать выражение 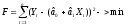Необходимые условия экстремума: Возьмем соответствующие производные и приравняем их к нулю: ;.

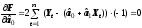Раскроем скобки и получим стандартную форму нормальных уравнений:

Решая систему уравнений относительно получаем их оценки:

Из последнего уравнения получаем: . Это равенство указывает на то, что уравнение регрессии проходит через точку . Обозначим. Подберем линейную функцию минимизирующую функционал . Это будет та же прямая, только в новых координатах, центр которых переместится в точку . Так как и .

Регрессионное уравнение имеет вид , где Xt – случайная величина, не коррелированная с ε. εt – случайная величина. Yt – объясняемая (зависимая) переменная, Xt – объясняющая (независимая) переменная. Поскольку Yt является суммой случайной переменной Xt и случайной переменной ε t , то она сама является случайной величиной. Основные гипотезы относительно модели:

1. - спецификация модели

2. Xt – случайная величина, не коррелированная с ε.

3. М(ε)=0

4. М(ε2)=σ2 = const - не зависит от t

5. M(εt, εs ) = 0 при t ≠ s – некоррелированность значений случайной составляющей в различные моменты времени

Условия 3, 4, 5 называются условиями Гаусса-Маркова

Прогноз будущего (или пропущенного) значения эндогенной переменной определяется по уравнению регрессии. Найдем доверительный интервал, который с доверительной вероятностью Р = 1 – α будет накрывать значение зависимой переменной Y^{^}:.

Доверительный интервал определяется разбросом случайной компоненты относительно уравнения регрессии. Причин этого разброса две:

• Оценки коэффициентов регрессии являются величинами случайными и они сами по себе создают разброс относительно истинного уравнения регрессии.

• Случайная составляющая ε_t

Ошибка предсказания равна

; ;

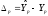
Тогда границы интервала будут задаваться так: (Y^ - tα*S∆p; Y^ + tα*S∆p), где tα - статистика Стьюдента.

20. Гетероскедастичность случайной компоненты. Тесты на наличие гетероскедастичности. (25 баллов)

Вторым условием Гаусса-Маркова для классической регрессионной модели является независимость дисперсии случайного члена от номера (момента) наблюдений (гомоскедастичность – одинаковый разброс). Нарушение этого условия принято называть гетероскедастичностью (неодинаковый разброс).

Явление гетероскедастичности возникает, как правило, при анализе неоднородных объектов. Например, при построении зависимости прибыли фирмы от размера основного фонда (или каких-либо других факторов) гетероскедастичность вызвана тем, что у больших фирм колебания прибыли будут выше, чем у малых.

МНК при наличии гетероскеда­стичности позволяет получить несмещенные оценки параметров модели, но оценка дисперсии ошибки, и, следовательно, границы доверительных интервалов оценок параметров модели и прогноза зависимой переменной будут неверными, т.к. они вычисляются на основании предположения гомоскедастичности ошибок.

Для проверки на гетероскедастичность существует большое число тестов. Мы остановимся на тсте Голдфельда-Квандта.

Тест Голдфелъда-Квандта применяется в том случае, ко­гда имеются предположения:

1. о прямой зависимости дисперсии σ_t, ошибки регрессии ε_t от величины некоторой независимой переменной X в наблюдении t;

2. случайный член ε_t, распределен нормально и не подвержен автокорреляции.

Алгоритм теста:

1. Упорядочивание n данных в выборке по величине независимой переменной, относительно которой есть подозрение на гетероскедастичность.

2. Исключение с средних наблюдений в этом упорядочении в целях построения двух независимых "частных" регрессий по данным n' = (n-с)/2 в начале выборки и по данным n' = (n - с)/2 в конце выборки

3. Проведение двух независимых "частных" регрессий - первых n' и последних n' наблюдений и построение соответствующих остатков е₁ и е₂;

3. Вычисление сумм квадратов остатков "частных" регрессий: е₁'е₁, е₂'е₂. Если предположение относительно природы гегероскедастичности верно, то дисперсии ошибок регрессии в последних n' наблюдениях будут больше (меньше), чем в первых n' наблюдениях при прямой (обратной) пропорциональной зависимости между σ_t и X_t и это скажется на сумме квадратов остатков в рассматриваемых частных регрессиях. Поэтому в качестве теста на выявление гетероскедастичности остатков регрессии предлагается использовать статистику F, вид кото­рой определяется предположением зависимости между диспер­сией ошибок регрессии σ_t и регрессором X_t:

F = е₁'е₁ / е₂'е₂- в случае обратной пропорциональности

F = е₂'е₂ / е₁'е₁- в случае прямой пропорциональности.

Статистика F имеет распределение Фишера с (n'- k- 1) степенями свободы, где k- число объясняющих переменных в регрессионном уравнении. Если значение статистики превышает критически значение при определенном уровне значимости, то нулевая гипотеза Н₀ об отсутствии гетероскедастичности отвергается.