ЭКОНОМЕТРИКА.

1. Анализ вариации зависимой переменной в регрессии.(25 баллов)(Лекция 2)= 4 вопросу

2. Тест Дарбина – Уотсона некоррелированности случайных возмущений в схеме Гаусса – Маркова. (25 баллов)

3. Метод имитационного моделирования. Исследование последствий нарушения условий теоремы Гаусса – Маркова. (25 баллов)

4. Анализ вариации зависимой переменной в регрессии.(25 баллов)

5. Коэффициент детерминации как мера качества спецификации эконометрической модели. (25 баллов)

6. Компьютерное моделирование эконометрических систем.(25 баллов)

7. F – Тест качества спецификации эконометрической модели. (25 баллов)

8. Процедура точечного прогнозирования по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной. (25 баллов)

9. Интервальное прогнозирование по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной. (25 баллов)

10. Множественная линейная регрессионная модель. Оценивание параметров множественной регрессии методом наименьших квадратов. (25 баллов)

11. Определение границ доверительных интервалов точечных оценок множественной регрессионной модели. (25 баллов)

12. Оценивание параметров модели взвешенным методом наименьших квадратов. (25 баллов)

13. Модель Марковица. (25 баллов)

14. Определение границ доверительного интервала прогноза зависимой переменной. (25 баллов)

15. Проверка гипотез относительно коэффициентов парной регрессии. (25

16. Автокорреляция случайного возмущения. (25 баллов)

17. Гетероскедастичность случайного возмущения. (25 баллов)

18. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели множественной регрессии. (25 баллов)

19. Модель парной регрессии. Границы доверительных интервалов.(25 баллов)

20. Гетероскедастичность случайной компоненты. Тесты на наличие гетероскедастичности. (25 баллов)

21. Автокорреляция случайной составляющей. Тесты на наличие автокорреляции. (25 баллов)

22. Спецификация и преобразование к приведенной форме динамических моделей. Лаговые и предопределенные переменные динамической модели. (25 баллов)

23. Уточнение эконометрических моделей путем датирования переменных.

24. Парная регрессия. Оценивание параметров методом наименьших квадратов. (25 баллов)

25. Тест Голдфелда – Квандта гомоскедастичности случайных возмущений в схеме Гаусса – Маркова. (25 баллов)

26. Дисперсионный анализ в парной регрессии. (25 баллов)

2. Тест Дарбина – Уотсона некоррелированности случайных возмущений в схеме Гаусса – Маркова. (25 баллов)

В классической регрессионной модели выполнение третьего условия Гаусса-Маркова (Соv(ε_t ε_S) = 0,при t ≠ s) гарантирует некоррелированность значений случайных членов в раз­личные моменты наблюдений и это позволяет получить несмещенные МНК-оценки с минимальной дисперсией. Зависимость значений случайных членов в различные моменты времени на­зывается автокорреляцией (сериальной корреляцией).

Формальной причиной автокорреляции в регрессионных моделях является нарушение третьего условия теоремы Гаусса-Маркова, действительной же причиной может быть: неправильная спецификация переменных (пропуск важной объясняющей переменной); использование ошибочной функциональной зависимости, а иногда и характер наблюдений (например, временные ряды).

Для проверки на автокорреляцию используется ряд крите­риев, из которых наиболее широкое применение получил крите­рий Дарбина-Уотсона:

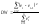
Критерий DW связан с выборочным коэффициентом корреляции между е_t и е_t-1, соотношением: DW≈2(1-r),

Если автокорреляция отсутствует, то DW ≈ 2, при наличии положительной автокорреляции DW<2, если автокорреляция отрицательна, DW>2. И поскольку коэффициент корреляции принимает значения -1 ≤ r ≤ 1, то 0≤ DW ≤ 4. Полученное для данной регрес­сии значение статистики сравнивается с верхней и нижней гра­ницами ее критического значения d_L ≤ d_крит ≤d_U. Границы d_U и d_L выбира­ются из таблиц по числу наблюдений n, числу регрессоров k и уровню значимости α. При этом возможны следующие случаи:

1. Наличие положительной автокорреляции: DW<d_L.

2. Наличие отрицательной автокорреляции: DW >4-d_L.

3. Автокорреляция отсутствует: d_U ≤ DW≤ 4-d_U.

Зоны неопределенности: d_L<DW< d_U или 4- d_U <DW<4-d_L.

3. Метод имитационного моделирования. Исследование последствий нарушения условий теоремы Гаусса – Маркова. (25 баллов)

Первая предпосылка теоремы Гаусса –Маркова: E (u₁) = E (u₂) = … = E (u_n). Ожидаемые значения случ возмущений равны м/у собой и равны 0. Это влечет св-во несмещенности оценок, найденных методом наименьших квадратов параметра a₀ и его точностных характеристик. Вообще, сущность метода ИМ состоит в воспроизведении n-раз ситуаций, в которых каждая из случайных возмущений (u₁,...,u_n) получает свое конкретное значение в заданных уравнениях наблюдения объекта какой-либо модели. При моделировании конкретных значений СВ U₁(j), U₂(j),..., U_n(j) в случае нарушения 1-ой предпосылки используется формула: U_i(j) = б_i * U^*_i(j) + m_i, но величина m_i выбирается константой, отличной от 0. Значения U^*_i(j) опр-ся по таблице «Значения независимых нормально распределенных стандартных случ переменных u₁^*, u₂^*, …, u_n^* по прошествии определенного числа опытов. Полученные значения U_i(j) исп-ся для получения оценочных значений, которые затем мы оцениваем с помощью МНК. Сравниваем полученные оценочные значения a₀ со значением исходного a₀. В случае сильного отличия (больше ошибки) считается, что коэф-т a₀ не обладает свойством несмещенности.

4. Анализ вариации зависимой переменной в регрессии=1

Рассмотрим вариацию (разброс) 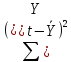значений 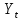вокруг среднего значения. Разобьем эту вариацию на две части: объясненную регрессионным уравнением и не объясненную (т.е. связанную с ошибками ).

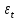Обозначим через 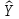t = + 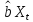предсказанное значение Yt, тогда

Yt — 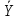— (Y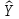t 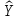- t) + (t - 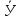) и вариация Yt представляется в виде трех слагаемых:

.

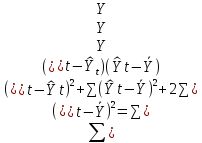Третье слагаемое равно нулю, так как у — 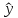= е, - вектор остатков регрессии, ортогонален константе г и вектору x. B самом деле, ∑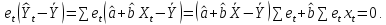 Поэтому верно равенство

(*)

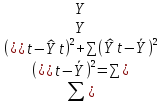TSS ESS RSS

Замечание. Вектор остатков регрессии ортогонален константе, т.е. г'е = ∑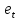= 0, вообще говоря, только в том случае, когда константа включена в число объясняющих параметров

регрессии. Поэтому (*) справедливо, вообще говоря, только в случае, когда константа включена в число объясняющих параметров регрессии.

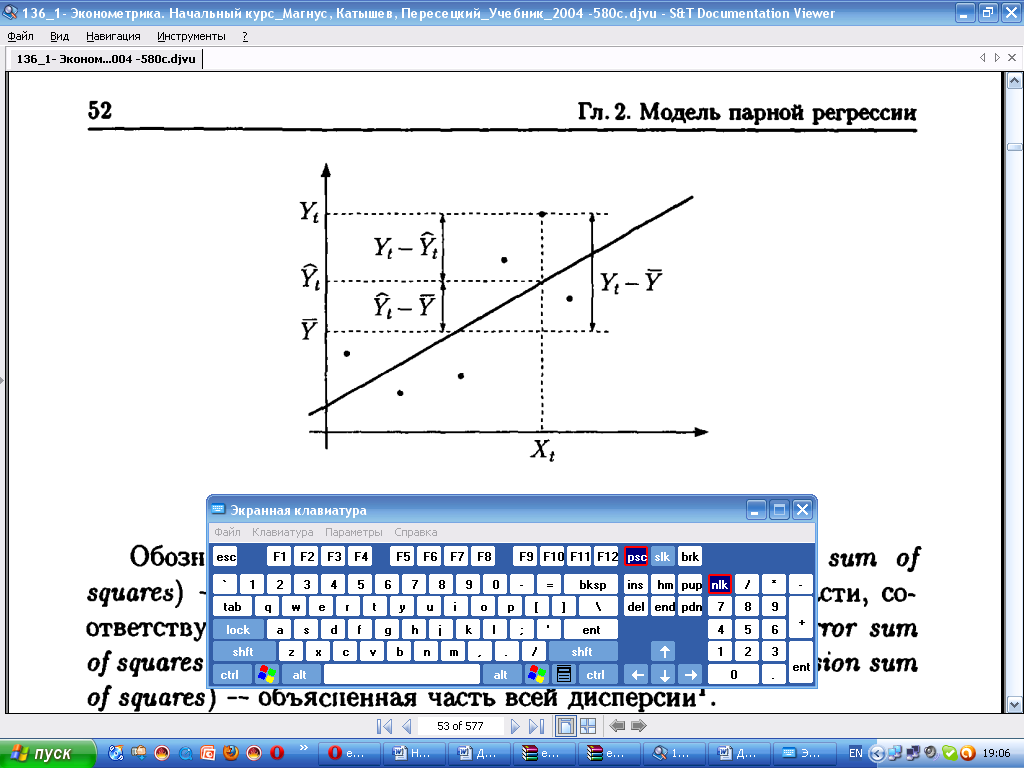
Обозначим левую часть в (*) через TSS (total sum of squares) — вся дисперсия, первое слагаемое в правой части, соответствующее не объясненной дисперсии, через ESS (error sum of squares), второе слагаемое в правой части — RSS (regression sum

of squares) — объясненная часть всей дисперсии.