Учреждение образования

«Минский государственный высший авиационный колледж»

Факультет гражданской авиации

Кафедра «Техническая эксплуатация воздушных судов и двигателей»

Курсовая работа

по дисциплине:

«Гидравлика»

Выполнил студент группы М208 Фёдоров Д.С.

Принял преподаватель Никончук А.Н.

17 Вариант

Минск 2011 г.

Оглавление

Оглавление 2

Введение 3

1.Теоретическая часть 4

2.Практическая часть 10

Заключение 24

Список использованной литературы 25

Введение

Гидравлика – это наука, изучающая законы равновесия и механического движения жидкостей и разрабатывающая методы применения этих законов для решения прикладных задач. Главнейшие области применения гидравлики – гидротехника, мелиорация и водное хозяйство, гидроэнергетика, водоснабжение и канализация, водный транспорт, машиностроение, авиация и т.д.

Данная курсовая работа выполняется с целью закрепления знаний, полученных при самостоятельном изучении дисциплины «Гидравлика», и приобретения практического применения этих знаний для решения инженерных задач.

Курсовая работа делится на две части: теоретическую и практическую. В теоретической части рассмотрены две темы: формирование параболического профиля скоростей на начальном участке ламинарного течения и неустановившееся течение жидкости. В практической части предусмотрено решение задач по следующим темам: определение давления в покоящейся жидкости; определение силы давления жидкости на плоские стенки; определение силы давления жидкость на криволинейные поверхности; относительный покой жидкости; решение задач с применением закона Архимеда; определение расхода при истечении жидкости через отверстия и насадки; применение уравнения Бернулли для решения задач механики.

Справочные данные, необходимые для решения задач, приведены в справочной литературе.

Курсовая работа выполнена после тщательного изучения, указанных выше тем, по перечисленной использованной литературе.

1. Теоретическая часть

Равномерное вращение сосуда с жидкостью.

В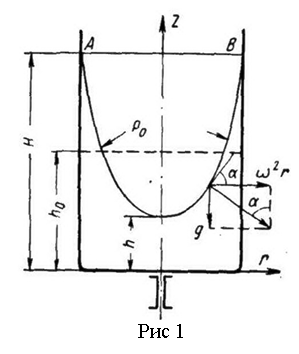озьмем открытый цилиндрический сосуд с жидкостью и сообщим ему постоянную угловую скорость вращения вокруг его вертикальной оси. Жидкость по- степенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится: в централь- ной части уровень жидкости понизится, у стенок — повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 1).

На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны и .

Равнодействующая массовая сила увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, в связи, с чем наклон этой поверхности с увеличением радиуса возрастает. Найдем уравнение кривой в системе координат и с началом в центре дна сосуда. Учитывая, что сила у является нормалью к кривой , из чертежа найдем, что

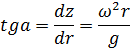
Отсюда

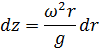
или после интегрирования

(1)

В точке пересечения кривой с осью вращения ,

поэтому окончательно будем иметь, т. е. кривая является параболой, а свободная поверхность жидкости — поверхностью параболоида вращения.

Пользуясь уравнением (1), можно определить положение свободной поверхности в сосуде, например максимальную высоту подъема жидкости и высоту расположения вершины параболоида при данной скорости вращения . Однако для этого необходимо использовать еще уравнение объемов: объем неподвижной жидкости равен ее объему во время вращения.

Н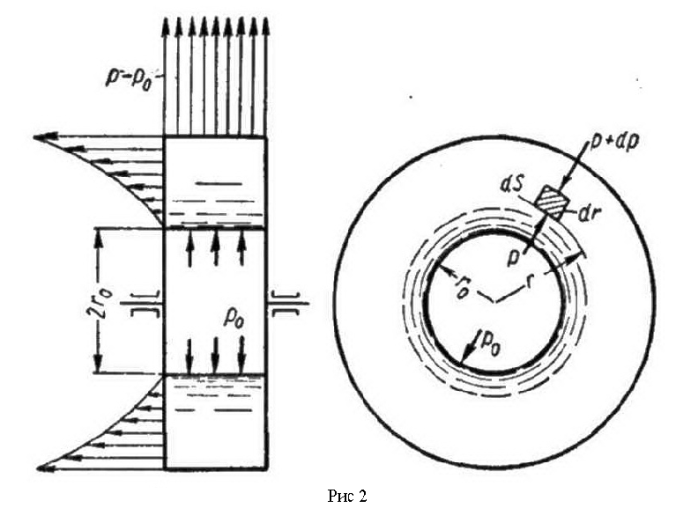а практике чаще все- го приходится иметь дело с таким случаем вращения сосуда с жидкостью, когда ось вращения расположена горизонтально (или произвольно), а угловая скорость столь велика, что силой тяжести можно пренебречь по сравнению с центробежными силами.

Закон изменения давления в жидкости для это- го случая легко получить из рассмотрения уравнения равновесия элементарного объема с площадью основания и высотой , взятой вдоль радиуса (рис. 2). На выделенный элемент жидкости действуют силы давления и центробежная сила. Обозначив давление в центре площадки , расположенной на радиусе , через , а в центре другого основания объема (на радиусе ) через , получим следующие уравнение равновесия выделенного объема в направлении радиуса:

,

или

.

После интегрирования

Постоянную найдем из условия, что при .

Следовательно,

Подставив ее значение в предыдущее уравнение, получим связь

между и в следующем виде:

(2)

Очевидно, что поверхностями уровня в данном случае будут цилиндрические поверхности с общей осью — осью вращения жидкости. Если сосуд лишь частично заполнен жидкостью, то ее свободная поверхность, как одна из поверхностей уровня, также будет цилиндрической, причем именно ее радиус, удобно обозначить через , а давление на ней через .

Часто бывает необходимо определить силу давления вращающейся вместе с сосудом жидкости на его стенку, нормальную к оси вращения (или на кольцевую часть этой стенки).

Для этого необходимо выразить сначала силу давления, приходящуюся на элементарную кольцевую площадку радиусом и шириной. Используя формулу (2), получим

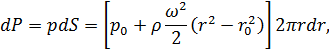
а затем следует выполнить интегрирование в требуемых пределах.

При большой скорости вращения жидкости можно получить весьма значительную суммарную силу давления на стенку. Это используется в некоторых фрикционных муфтах, где для осуществления сцепления двух валов требуется создание больших сил нормального давления. Способом, указанным выше, пользуются для подсчета силы осевого давления жидкости на рабочие колеса центробежных насосов.

Те же формулы для рассмотренного случая относительного покоя можно вывести путем интегрирования дифференциального уравнения равновесия жидкости. Поместив начало

координат в центре дна сосуда и направив ось вертикально вверх, получим

;

; .

Подставляя эти величины в уравнение, получим

,

или

.

Если учесть, что

,

то после интегрирования

.

При и , следовательно,

.

В результате окончательно получим

.

Уравнение свободной поверхности жидкости может быть по- лучено, если в этом уравнении положить . После сокращений и преобразования

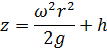
что вполне совпадает с ранее полученной формулой (1).

Если в предыдущем выводе пренебречь си- лой тяжести , а постоянную интегри- рования определить из условия, что при , , то получим уже известную формулу (2).