
- •1. Парная регрессия
- •1.1. Спецификация модели
- •1.2. Парная линейная регрессия. Оценка параметров. Экономическая интерпретация
- •1.3. Основные предположения регрессионного анализа
- •1.4. Статистические свойства оценок. Проверка статистической значимости в парной линейной регрессии
- •1.5. Доверительные интервалы для оценок параметров. Доверительные интервалы прогноза для парной линейной регрессии
- •1.6. Метод Гольдфельда—Квандта проверки гипотезы гомоскедастичности
- •2. Множественная регрессия
- •2.1. Спецификация модели
- •2.2. Множественная линейная регрессия. Оценка параметров. Экономическая интерпретация
- •3. Системы одновременных уравнений
- •4. Временные ряды
- •4.1. Компоненты временных рядов
- •4.2. Критерии случайности
- •4.3. Оценка тренда и периодической составляющей
- •4.4. Критерий Дарбина—Уотсона
- •4.5. Сглаживание временного ряда с помощью простой скользящей средней
- •4.6. Сглаживание временного ряда с помощью взвешенной скользящей средней
- •4.7. Сглаживание временного ряда с помощью скользящей медианы
- •5. Практические задания
- •5.1. Лабораторная работа № 1. Парная линейная регрессия
- •5.2. Лабораторная работа № 2. Метод Гольдфельда—Квандта проверки гипотезы гомоскедастичности
- •5.3. Лабораторная работа № 3. Множественная линейная регрессия
- •5.4. Лабораторная работа № 4. Макроэкономическая модель Кейнса
- •5.5. Лабораторная работа № 5. Проверка случайности ряда наблюдений
- •5.6. Лабораторная работа № 6. Оценка тренда и периодической составляющей
- •5.7. Лабораторная работа № 7. Сглаживание временного ряда с помощью простой скользящей средней
- •5.8. Лабораторная работа № 8. Критерий Дарбина—Уотсона
- •5.9. Лабораторная работа № 9. Подбор и оценка тренда с помощью встроенных средств Excel
- •5.10. Тест по парной и множественной регрессии
- •6. Рекомендуемая литература
- •8. Приложения. Статистические таблицы
- •8.1. Приложение 1. Стандартное нормальное распределение
- •8.2. Приложение 2. Критические значения -критерия Стьюдента
- •8.3. Приложение 3. Критические значения -критерия Фишера
- •8.4. Приложение 4. Критические значения статистики Дарбина—Уотсона
- •8.5. Приложение 5. Критические значения распределения
- •199034, С.-Петербург, Университетская наб., 7/9
- •199061, С.-Петербург, Средний пр., 41.
1.2. Парная линейная регрессия. Оценка параметров. Экономическая интерпретация
В практике
эконометрического анализа чаще всего
используют линейную парную регрессию,
т.е. между показателем и фактором
предполагается зависимость вида
![]() .
Условие нахождения коэффициентов
эмпирической регрессии (т.е. функциональной
зависимости вида
.
Условие нахождения коэффициентов
эмпирической регрессии (т.е. функциональной
зависимости вида
![]() )
по методу наименьших квадратов для
парной линейной регрессии записывается
следующим образом:
)
по методу наименьших квадратов для
парной линейной регрессии записывается
следующим образом:
![]() .
.
Вычисляя производные
функции
![]() по
неизвестным параметрам
по
неизвестным параметрам
![]() и приравнивая их к нулю, приходим к
следующей системе из двух уравнений,
линейной относительно неизвестных
и приравнивая их к нулю, приходим к
следующей системе из двух уравнений,
линейной относительно неизвестных
![]() :
:
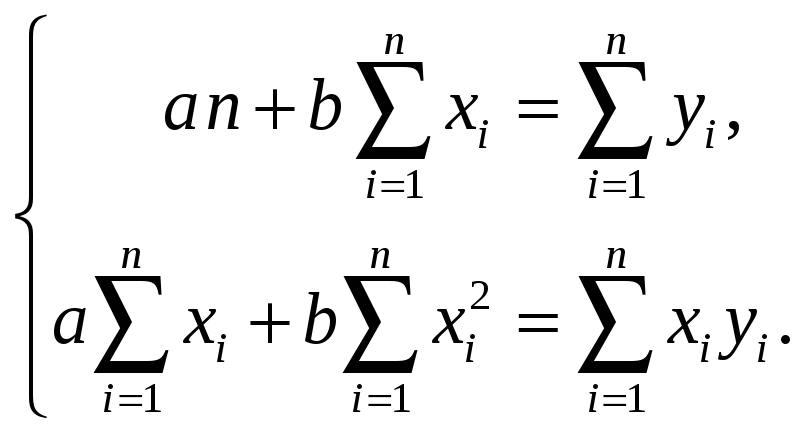
Решение этой
системы линейных уравнений (т.е. значения
![]() является оценкой неизвестных параметров
является оценкой неизвестных параметров
![]() и
и
![]() по методу наименьших квадратов, его
можно найти по формулам
по методу наименьших квадратов, его
можно найти по формулам
![]()
где
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
С помощью понятий выборочной дисперсии, ковариации и корреляции это решение можно записать специальным образом:
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() — выборочные средние,
— выборочные средние,
![]() ,
,
![]() — выборочные дисперсии,
— выборочные дисперсии,
 — выборочный коэффициент корреляции.
— выборочный коэффициент корреляции.
Таким образом, парная линейная регрессия имеет вид
![]() .
.
С помощью этого уравнения нетрудно определить расчетные значения показателя, для значений объясняющего фактора, которые содержатся в выборке:
![]() ,
,
![]() .
.
Для проверки статистической значимости парной линейной регрессии используются остатки (разности между фактическими значениями показателя и значениями, вычисленными по уравнению линейной регрессии):
![]()
![]() .
.
Найденному
коэффициенту
![]() при объясняющем факторе
при объясняющем факторе
![]() в парной линейной регрессии можно дать
естественную экономическую интерпретацию.
Коэффициент при объясняющем факторе
показывает, на какую величину изменяется
в среднем изучаемый эконометрический
показатель при увеличении значения
объясняющего фактора на одну единицу.
в парной линейной регрессии можно дать
естественную экономическую интерпретацию.
Коэффициент при объясняющем факторе
показывает, на какую величину изменяется
в среднем изучаемый эконометрический
показатель при увеличении значения
объясняющего фактора на одну единицу.
1.3. Основные предположения регрессионного анализа
Основные предположения
регрессионного анализа относятся к
случайной компоненте
![]() и имеют решающее значение для правильного
и обоснованного применения регрессионного
анализа в эконометрических исследованиях.
и имеют решающее значение для правильного
и обоснованного применения регрессионного
анализа в эконометрических исследованиях.
В классической модели регрессионного анализа предполагаются выполненными следующие предположения:
1) Величины
![]() являются случайными и образуют слабый
белый шум — последовательность
центрированных (
являются случайными и образуют слабый
белый шум — последовательность
центрированных (![]() )
и некоррелированных (
)
и некоррелированных (![]() )
случайных величин с одинаковыми
дисперсиями (
)
случайных величин с одинаковыми
дисперсиями (![]() ).
Последнее условие называется условием
гомоскедастичности. Нарушение этого
условия называется гетероскедастичностью.
).
Последнее условие называется условием
гомоскедастичности. Нарушение этого
условия называется гетероскедастичностью.
2) Величины
![]() взаимно независимы со значениями
объясняющих переменных.
взаимно независимы со значениями
объясняющих переменных.
Эти два предположения образуют первую группу предположений, необходимых для проведения регрессионного анализа в рамках классической модели.
Вторая группа предположений дает достаточные условия для обоснованного проведения проверки статистической значимости эмпирических регрессий:
3) Совместное
распределение случайных величин
![]() является нормальным.
является нормальным.
При выполнении
предположений первой и второй групп
случайные величины
![]() оказываются взаимно независимыми,
одинаково распределенными случайными
величинами, подчиняющимися нормальному
распределению с нулевым математическим
ожиданием и дисперсией
оказываются взаимно независимыми,
одинаково распределенными случайными
величинами, подчиняющимися нормальному
распределению с нулевым математическим
ожиданием и дисперсией
![]() .
.
1.4. Статистические свойства оценок. Проверка статистической значимости в парной линейной регрессии
При выполнении
предположений первой группы можно
доказать теорему Гаусса—Маркова о том,
что оценки наименьших квадратов
![]() неизвестных параметров
неизвестных параметров
![]() являются несмещенными оценками с
минимальными дисперсиями в классе
линейных оценок.
являются несмещенными оценками с
минимальными дисперсиями в классе
линейных оценок.
Можно также
показать, что статистика
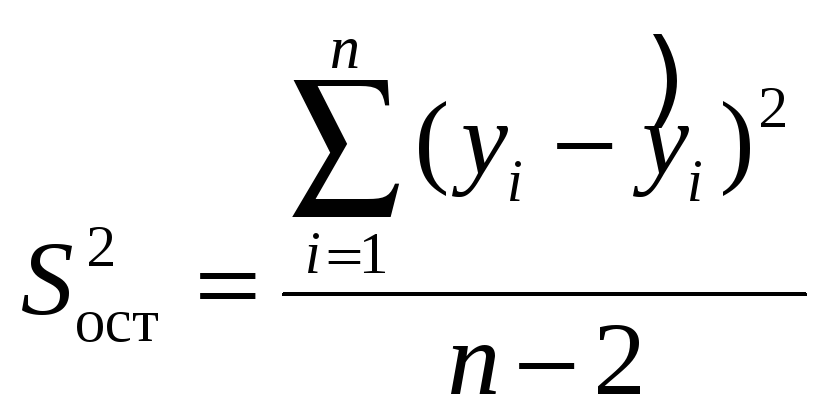 является несмещенной оценкой дисперсии
является несмещенной оценкой дисперсии
![]() .
.
При выполнении предположений первой и второй групп справедливы утверждения:
1)
Статистика
![]() распределена
по закону Стьюдента с
распределена
по закону Стьюдента с
![]() степенями свободы (т.е.
степенями свободы (т.е.
![]() ),
где
),
где
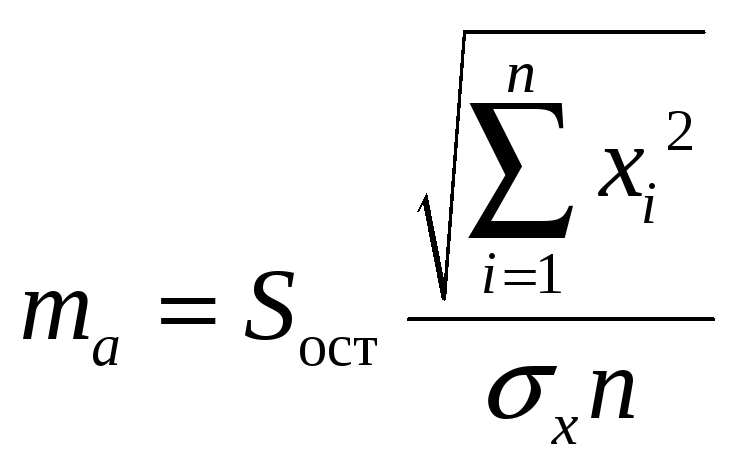 ,
,
![]() .
.
2) Статистика
![]() распределена по закону Стьюдента с
распределена по закону Стьюдента с
![]() степенями свободы (т.е.
степенями свободы (т.е.
![]() ),
где
),
где
![]() ,
,
![]() .
.
Правило проверки
статистической значимости оценок
![]() и
и
![]() основывается
на проверке статистических гипотез
основывается
на проверке статистических гипотез
![]() и
и
![]() при альтернативных гипотезах
при альтернативных гипотезах
![]() и
и
![]() .
Невозможность отклонения какой-либо
из гипотез
.
Невозможность отклонения какой-либо
из гипотез
![]() в пользу альтернативной означает
статистическую незначимость
соответствующего коэффициента и,
наоборот, отклонение какой-либо из
гипотез
в пользу альтернативной означает
статистическую незначимость
соответствующего коэффициента и,
наоборот, отклонение какой-либо из
гипотез
![]() означает, что соответствующий коэффициент
статистически значим.
означает, что соответствующий коэффициент
статистически значим.
Проверка значимости оценок с помощью критерия Стьюдента проводится путем сопоставления вычисленных значений оценок с величиной их стандартной ошибки.
Для проверки
значимости оценок необходимо вычислить
значения
![]() -статистик:
-статистик:
![]() ,
,
где
 ,
,
![]() ,
,
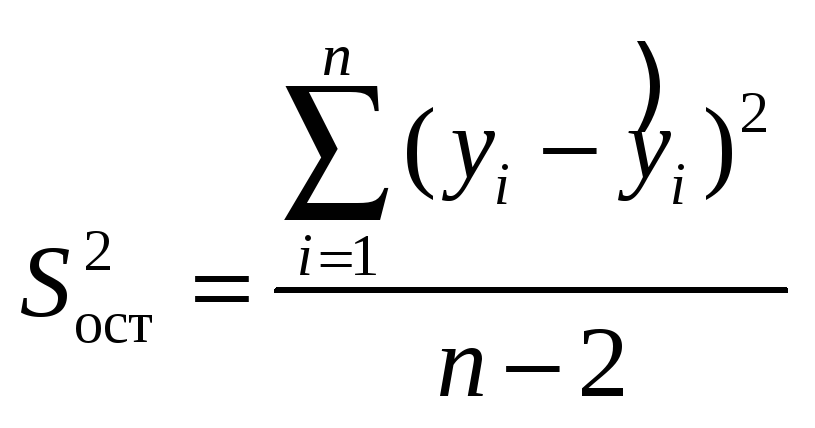 ,
,
![]() .
.
Правило проверки
значимости коэффициента
![]()
Статистика
![]() при выполнении гипотезы
при выполнении гипотезы
![]() распределена по закону Стьюдента с
распределена по закону Стьюдента с
![]() степенями
свободы, поэтому:
степенями
свободы, поэтому:
1) если
![]() ,
то гипотезу
,
то гипотезу
![]() следует отклонить и, следовательно,
признать коэффициент
следует отклонить и, следовательно,
признать коэффициент
![]() статистически
значимым;
статистически
значимым;
2) если
![]() ,
то гипотезу
,
то гипотезу![]() следует принять и, следовательно,
признать коэффициент
следует принять и, следовательно,
признать коэффициент
![]() статистически незначимым.
статистически незначимым.
Значение
![]() определяется по таблице распределения
Стьюдента при
определяется по таблице распределения
Стьюдента при
![]() степенях свободы как критическая точка,
соответствующая двусторонней критической
области с уровнем значимости 5%.
степенях свободы как критическая точка,
соответствующая двусторонней критической
области с уровнем значимости 5%.
Правило проверки
значимости коэффициента
![]()
Статистика
![]() при выполнении гипотезы
при выполнении гипотезы
![]() распределена по закону Стьюдента с
распределена по закону Стьюдента с
![]() степенями свободы, поэтому:
степенями свободы, поэтому:
1) если
![]() ,
то гипотезу
,
то гипотезу
![]() следует отклонить и, следовательно,
признать коэффициент
следует отклонить и, следовательно,
признать коэффициент
![]() статистически значимым;
статистически значимым;
2)
если
![]() ,
то гипотезу
,
то гипотезу
![]() следует принять и, следовательно,
признать коэффициент
следует принять и, следовательно,
признать коэффициент
![]() статистически незначимым.
статистически незначимым.
Значение
![]() определяется по таблице распределения
Стьюдента при
определяется по таблице распределения
Стьюдента при
![]() степенях свободы как критическая точка,
соответствующая двусторонней критической
области с уровнем значимости 5%.
степенях свободы как критическая точка,
соответствующая двусторонней критической
области с уровнем значимости 5%.
Аналогично проверяется значимость коэффициента парной корреляции.
Если совместное
распределение показателей
![]() нормально и выполнена гипотеза
нормально и выполнена гипотеза
![]() ,
то статистика
,
то статистика
![]() распределена по закону Стьюдента с
распределена по закону Стьюдента с
![]() степенями свободы. Здесь
степенями свободы. Здесь
![]() — теоретический коэффициент парной
корреляции,
— теоретический коэффициент парной
корреляции,
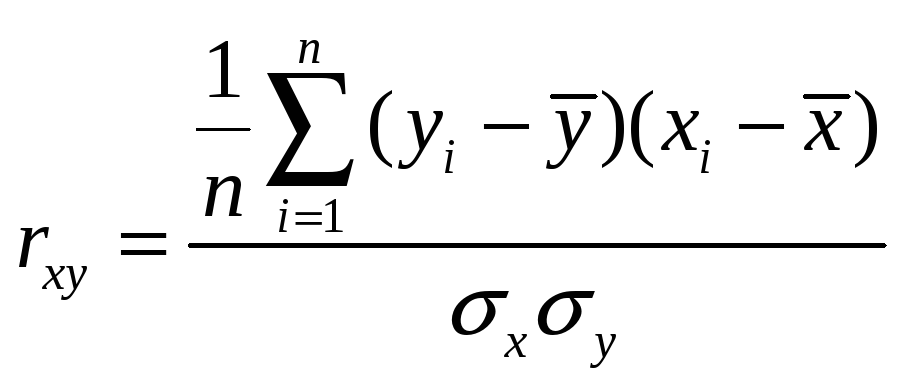 — выборочный коэффициент парной
корреляции,
— выборочный коэффициент парной
корреляции,
![]() ,
,
![]() .
.
Правило проверки
значимости коэффициента
![]()
Вычислить значение
статистики
![]() :
:
1) если
![]() ,
то гипотезу
,
то гипотезу
![]() следует отклонить и, следовательно,
признать коэффициент
следует отклонить и, следовательно,
признать коэффициент
![]() статистически значимым;
статистически значимым;
2) если
![]() ,
то гипотезу
,
то гипотезу
![]() следует принять и, следовательно,
признать коэффициент
следует принять и, следовательно,
признать коэффициент
![]() статистически незначимым.
статистически незначимым.
Значение
![]() определяется по таблице распределения
Стьюдента при
определяется по таблице распределения
Стьюдента при
![]() степенях свободы как критическая точка,
соответствующая двусторонней критической
области с уровнем значимости 5%.
степенях свободы как критическая точка,
соответствующая двусторонней критической
области с уровнем значимости 5%.
Заметим, что
проверка значимости коэффициента
![]() одновременно является проверкой
значимости парной линейной регрессии
в целом.
одновременно является проверкой
значимости парной линейной регрессии
в целом.
Еще один способ
проверки значимости парной линейной
регрессии основан на коэффициенте
детерминации
![]() и статистике, распределенной по закону
Фишера с числом степеней свободы
числителя равным 1 и числом степеней
свободы знаменателя
и статистике, распределенной по закону
Фишера с числом степеней свободы
числителя равным 1 и числом степеней
свободы знаменателя
![]() .
Коэффициент детерминации вычисляется
по формуле
.
Коэффициент детерминации вычисляется
по формуле
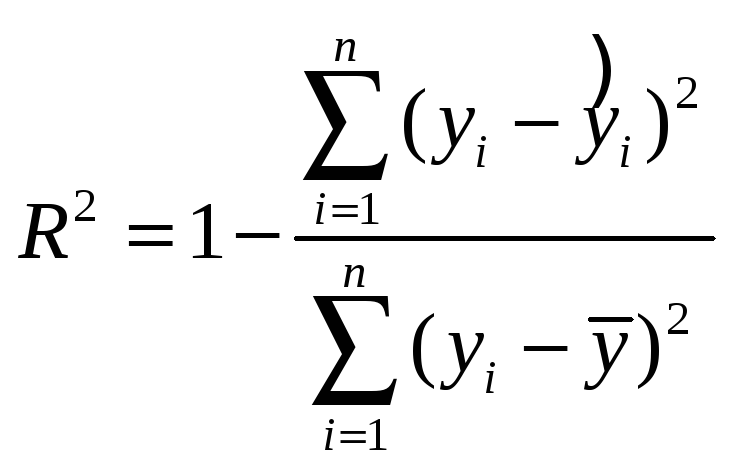 .
.
Если выполнены
предположения регрессионного анализа,
то при выполнении гипотезы
![]() (что означает отсутствие взаимосвязи
между
(что означает отсутствие взаимосвязи
между
![]() и
и
![]() ,
а также статистическую незначимость
построенной парной регрессии) статистика
,
а также статистическую незначимость
построенной парной регрессии) статистика
![]() распределена по закону Фишера с числом
степеней свободы числителя равным
единице и числом степеней свободы
знаменателя равным
распределена по закону Фишера с числом
степеней свободы числителя равным
единице и числом степеней свободы
знаменателя равным
![]() (т.е.
(т.е.
![]() ).
).
Правило проверки
значимости линейной регрессии в целом
(гипотезы
![]() )
с использованием
)
с использованием
![]() статистики
статистики
Вычислить значение
статистики
![]() :
:
1) если
![]() ,
то гипотезу
,
то гипотезу
![]() следует отклонить и, следовательно,
признать построенное уравнение линейной
регрессии статистически значимым;
следует отклонить и, следовательно,
признать построенное уравнение линейной
регрессии статистически значимым;
2) если
![]() ,
то гипотезу
,
то гипотезу
![]() следует принять и, следовательно,
признать построенное уравнение
статистически незначимым.
следует принять и, следовательно,
признать построенное уравнение
статистически незначимым.
Значение
![]() определяется как критическая точка по
таблице распределения Фишера при числе
степеней свободы числителя равном 1 и
числе степеней свободы знаменателя
равном
определяется как критическая точка по
таблице распределения Фишера при числе
степеней свободы числителя равном 1 и
числе степеней свободы знаменателя
равном
![]() с уровнем значимости 5%.
с уровнем значимости 5%.
