3. Синтез регулятора и наблюдателя на основе задания желаемых собственных значений замкнутой системы.

Построение управления в виде линейной обратной связи в рассмотренном выше примере осуществлялось в предположении, что исходной моделью объекта управления является линейная система с полной информацией, т.е. для измерения доступен весь вектор целиком, а, следовательно, весь вектор может быть использован для анализа и синтеза управления. Однако чаще встречаются ситуации, когда для измерения доступен не весь вектор состояния , а лишь некоторые линейные комбинации его компонент (в общем случае могут измеряться зависимости ). Это связано с тем, что некоторые из переменных состояния могут являться абстрактными, не иметь физических аналогов в реальной системе или же не могут быть измерены. Это означает, что устройство, измеряющее и фиксирующее состояние компонент вектора непрерывно в любой момент времени или в некоторые дискретные моменты, отсутствует, однако есть устройство, измеряющее некоторые другие параметры функционирования системы и определяемое моделью .

Таким образом, возникает вопрос: можно ли определить вектор состояния по измеряемому вектору выхода?

В предыдущем примере выполнялось равенство , а в общем случае линейная модель объекта управления имеет вид:

где – вектор состояний системы управления, – вектор измерений, называемым вектором выхода, а – вектор управляющих воздействий, называемый вектором входа системы. Предположим дополнительно, что .

В этом случае найти управление в виде обратной связи , воспользовавшись рассмотренными способами, уже невозможно, и задача синтеза управления требует решения двух отдельных задач. Во-первых, необходимо построить устройство, формирующее оценку вектора состояния на основе информации о нем в виде измеряемых величин ­ компонент вектора . Во-вторых, сформировать, используя полученную оценку, управление в виде обратной связи .

На первом этапе оценка вектора состояния строится как решение системы

При этом оценка должна быть такова, что при . Такая динамическая система называется асимптотическим наблюдателем, матрица неизвестна и, пока она не задана, уравнения наблюдателя не определены, поэтому для формирования наблюдающего устройства необходимо найти матрицу .

На втором этапе формируется управление , при известной оценке вектора состояния в этой задаче требуется найти матрицу коэффициентов .

Рассматривая совместно исходную систему с уравнениями наблюдателя и управлением , получим замкнутую систему:

Сделав замену переменных и можно перейти к системе

где выполняется условие при , и матрицы и необходимо построить, исходя из этого условия. Поскольку это означает, что полученная линейная система должна быть асимптотически устойчивой, а это определяется нахождением ее собственных чисел в открытой левой полуплоскости (их вещественная часть должна быть отрицательна).

Матрица системы имеет блочную структуру, которая позволяет осуществить поиск неизвестных матриц и как решений задач формирования линейной связи по вектору состояния отдельно для линейных систем

(4.3.1)

и

(4.3.2)

соответственно, построив для первой из них управление в виде обратной связи по вектору состояния (стабилизирующее управление), а для второй (стабилизирующее управление). Указанным образом определяются неизвестные матрицы и . Это может быть сделано, если обе системы стабилизируемы, т.е. собственные значения их неуправляемых частей имеют отрицательные вещественные части. При этом неуправляемые полюса второй системы являются ненаблюдаемыми полюсами исходной модели. Для нахождения матриц и могут быть, например, применены методы, основанные на задании желаемых собственных чисел замкнутой системы, или методы оптимальной стабилизации.

Теперь можно сформировать регулятор ­ динамическую систему, формирующую оценку и управление в виде:

(4.3.3)

где – вектор оценок компонент вектора состояний исходной системы управления ­ вектор состояния регулятора, – входной вектор регулятора, а – выходной вектор регулятора.

Для известных матриц и формирование такого регулятора легко осуществить с помощью функции reg. Для применения этой функции исходный LTI-объект должен быть представлен в ss-форме. Тогда указанная функция вызывается командой rsys=reg(sys,-K,L), где sys ­ исходный LTI-объект в ss-форме. Результатом является LTI-модель (4.3.3).

С помощью функции estim можно отдельно сформировать уравнения наблюдателя Функция вызывается командой rsys= estim(sys,L) и, также как и функция reg предполагает, что исходный LTI-объект должен быть представлен в ss-форме.

Также формирование регулятора и наблюдателя можно осуществить, не используя дополнительно специальные функции.

Пример 4.3.1.

Введем исходные матрицы системы (,,):

>> A=[-1 0 0; 0 -2 1; -1 0 2]

B=[0; 0; -1]

C=[0 0 1]

A =

-1 0 0

0 -2 1

-1 0 2

B =

0

0

-1

C =

0 0 1

D=0

Выделим управляемую подсистему и проверим, что полюса неуправляемой части находятся в открытой левой полуплоскости комплексной плоскости:

>> S1=ctrb(A,B);

m=rank(S1)

m =

2

>> [A1,B1,C1,Tc,kc] = ctrbf(A,B,C)

A1 =

-1 0 0

0 -2 -1

1 0 2

B1 =

0

0

-1

C1 =

0 0 1

Tc =

-1 0 0

0 -1 0

0 0 1

kc =

1 1 0

Выделяем управляемая подсистему:

>> Ac=A1(2:3,2:3)

Ac =

-2 -1

0 2

>> Bc=B(2:3,:)

Bc =

0

-1

>> Anc=A1(1,1)

Anc =

-1

Сформируем матрицу :

>> p=[-1;-2];

>> K0=place(Ac,Bc,p)

place: ndigits= 15

K0 =

[0 -3]

>> K1=[0 K0]

K1 =

0 0 -3

>> K1=-K1;

Cl1=A1+B1*K1;

>> K=K1*Tc;

eigcl=eig(A+B*K)

eigcl =

-2

-1

-1

Построим матрицы в системе (4.3.2)

>>A'

ans =

-1 0 -1

0 -2 0

0 1 2

>> -C'

ans =

0

0

-1

Проверим, является ли система управления с этими матрицами полностью управляемой

>> S2=ctrb(A’,-C’);

m=rank(S2)

m =

2

Матрица имеет одно неуправляемое собственное число (оно же является ненаблюдаемым числом матрицы исходной системы ), равное :

>> [A2,B2,C2,Tc2,kc2] = ctrbf(A’,-C’,B’);

>> Anc2=A2(1,1)

Anc2 =

-2

>> Ac2=A2(2:3,2:3);Bc2=B2(2:3,:);

>> p=[-2;-3]

p =

-2

-3

Сформируем матрицу :

>> L0=place(Ac2,Bc2,p);

place: ndigits= 15

>>L1=[0 L0]; L1=-L1; L=L1*Tc2;

>> eigcl=eig(A'-C'*L)

eigcl =

-2.0000

-3.0000

-2.0000

>> L=L';

>> eig(A-L*C)

ans =

-2.0000

-2.0000

-3.0000

>> save exnFI A B C K L;

Таким образом, с помощью метода задания желаемых полюсов замкнутой системы, сформированы, соответственно, матрица и матрица , которая обеспечивает собственные значения наблюдателя и , еще одним собственным значением наблюдателя будет ненаблюдаемое число исходной системы.

Теперь можно построить регулятор непосредственно проведя вычисления матриц, представляющих его в пространстве состояний { Ac, Bс, Cс, Dс}:

>> Ac=A+B*K-L*C; Bc=L; Cc=K; Dc=0;

Иначе указанные матрицы можно сформировать с помощью функции reg:

>>sys=ss(A,B,C,D);

>>rsys=reg(sys,-K,L);

>> Ac=rsys.a

Ac =

-1 0 0

0 -2 1

-1 0 -5

>> Bc=rsys.b

Bc =

0

0

4

>> Cc=rsys.c

Cc =

-2 0 6

>> Dc=rsys.d

Dc =

0

На рис. 4.3.1 приводится Simulink-модель, моделирующая динамику замкнутой системы c неполной информацией для рассмотренных выше исходных данных и найденных матриц и .

Аналогично предыдущему примеру модель включает в себя (рис. 4.3.2) блок формирования линейной модели объекта управления (State-Space), входом этого блока является вектор управлений , а выходом ­ вектор , в качестве вектора начальных данных возьмем вектор , блок (рис. 4.3.3), формирующий LTI-модель регулятора (Controller). Входы и выходы указанных блоков соединены между собой и образуют замкнутую систему

Кроме того, модель содержит блоки вывода результатов моделирования (Scope1) в виде графиков функций компонент векторов и . На рис. 4.3.4 показан график функции, полученный в результате моделирование динамики замкнутой системы .

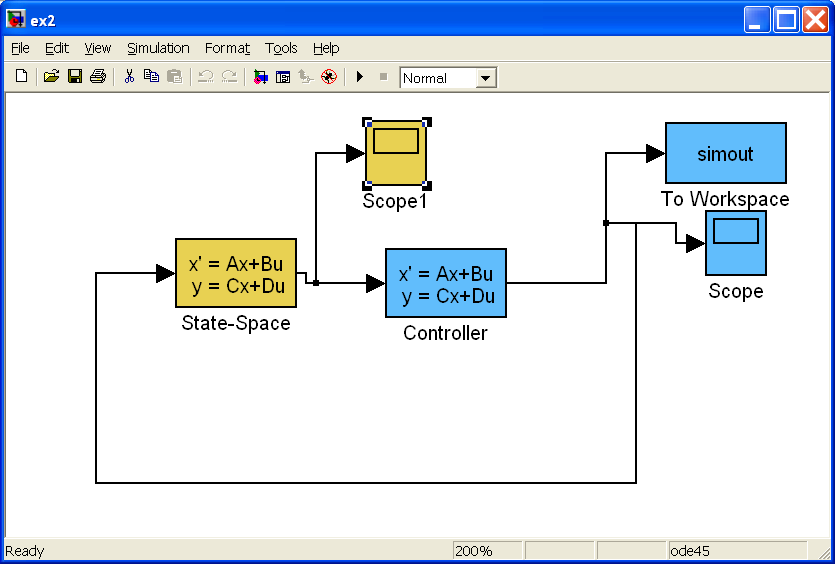
Рис. 4.3.1 Simulink-модель

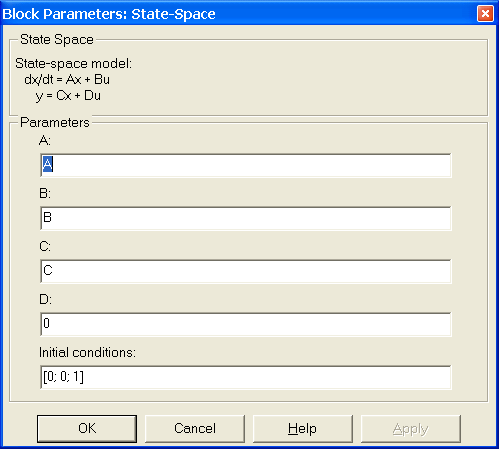
Рис. 4.3.2. Блок формирования исходной LTI-модели sys

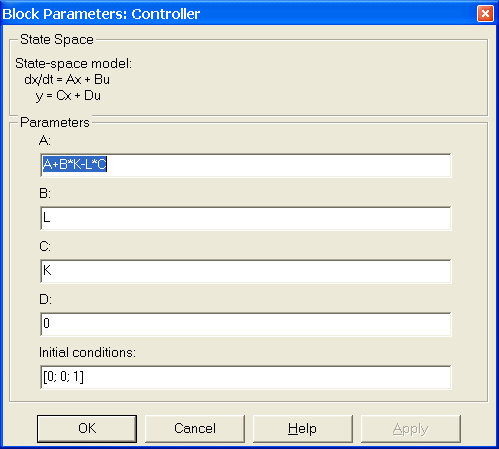
Рис. 4.3.3. Блок формирования LTI-модели регулятора

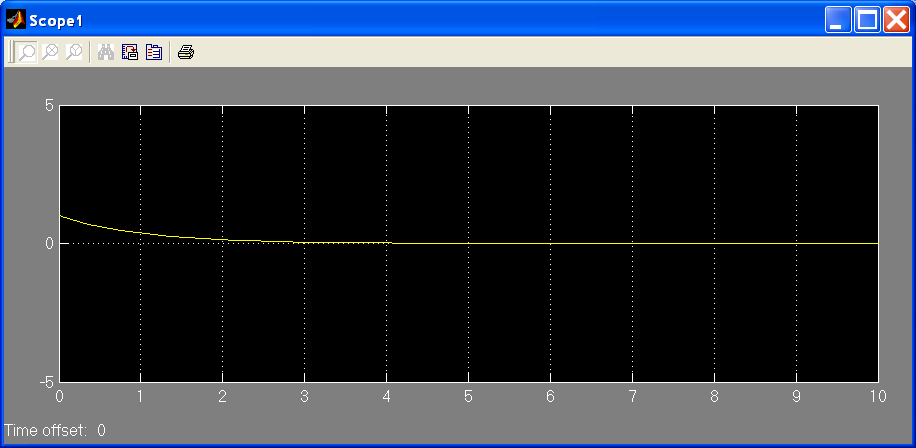
Рис. 4.3.4. График функции

Изменяя значения компонент матриц и , можно повлиять на переходный процесс выхода .

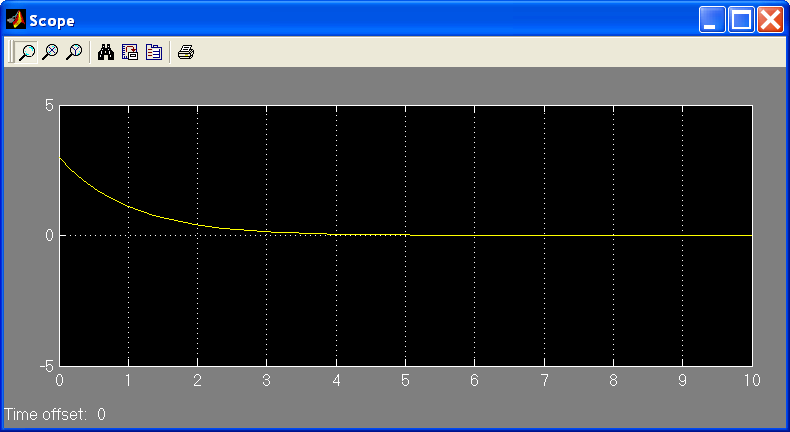
Рис. 4.3.5. График функции