2. Синтез стабилизирующего управления (регулятора) на основе задания желаемых собственных значений (полюсов) замкнутой системы.

Расположение полюсов в замкнутой системе влияет на ее различные динамические свойства: время переходного процесса, показатели колебательности и так далее. Поэтому методы построения стабилизирующего управления, основанные на задании собственных чисел замкнутой системы, позволяют воздействовать на указанные характеристики замкнутой системы. Приведем ряд функций, которые могут быть использованы для формирования управления в виде обратной линейной связи на основе задания полюсов (собственных значений) замкнутой системы.

Будем считать, что исходной моделью объекта управления является линейная система с полной информацией:

Функция place предназначена для расчета коэффициентов матрицы обратной связи таких, что матрица замкнутой системы имеет заданные собственные значения. Функция вызывается командой place(A,B,p) или оператором K=place(A,B,p), где p ­ вектор, содержащий задаваемые собственные значения и имеющий размерность, равную размерности вектора состояния. Использование функции place предполагает, что система полностью управляема.

>> a=[1 2; 0 2]; b=[2 0; 0 1]; p=[-1;-2];

>> K=place(a,b,p)

place: ndigits= 15

K =

1 1

0 4

>> eig(a-b*K)

ans =

-2

-1

Функция acker в свою очередь предназначена для расчета коэффициентов матрицы обратной связи для скалярного управления, т.е. , однако для этого можно применить и рассмотренную выше функцию place. Функция вызывается командой acker(A,B,p) или оператором k=place(A,B,p), где p ­ вектор, содержащий задаваемые собственные значения и имеющий размерность, равную размерности вектора состояния. Использование функции acker также предполагает, что система полностью управляема.

>>a=[1 2; 0 2]; b=[1;0]; p=[-1;-2];

>> k=acker(a,b,p)

k =

3 6

>> eig(a-b*k)

ans =

-1.0000

-2.0000

Рассмотрим пример формирования управления в виде обратной связи ­ стабилизирующего управления для системы, которая не является полностью управляемой.

Пример 4.2.1.

>>clear all

Введем матрицы системы с полной информацией , размерность вектора состояния равна пяти, размерность вектора управлений двум.

>>A=[-1 1 0 -1 0; 1 0 0 1 1; 0 0 0 0 -3; 0 0 0 -1 0; 0 0 1 1 -1];

>>B=[ 0 0; 1 0; 0 1; 0 0; 0 0]; C=eye(5);

Построим матрицу управляемости.

>>S=ctrb(A,B);

Ранг матрицы управляемости равен четырем, следовательно, в системе имеется одно неуправляемое число. Если окажется, что это собственное число имеет отрицательную вещественную часть, то для построения стабилизирующего управления необходимо сформировать каноническую форму управляемости и, выделив полностью управляемую подсистему, сформировать для нее линейную обратную связь, найдя ее коэффициенты с помощью функции place. Затем сформировать обратную связь для полной системы, представленной в канонической форме управляемости, дополнив матрицу обратной связи столбцом с любыми элементами, стоящим на первом месте. Затем выполнить обратную замену переменных, преобразовав матрицу обратных связей.

>>m=rank(S); % m=4

Каноническая форма управляемости:

>>[A1,B1,C1,T]=ctrbf(A,B,C);

Управляемая подсистема :

>>Ac=A1(2:5,2:5);

>>Bc=B1(2:5,:);

Неуправляемая подсистема :

>>Anc=A1(1,1);

Собственное значение неуправляемой части ­ матрицы nceig = -1 ­ отрицательно:

>>nceig=eig(Anc);

>>Sc=ctrb(A1,B1); % Matrix of controllability - matrica upravlaemosti

>>mc=rank(Sc); % mc=4 - full controllability

Зададим вектор желаемых собственных значений управляемой подсистемы :

>>p=[-1;-1; -2; -2];

>>Kc=place(Ac,Bc,p);

>>Kc=-Kc;

Сформируем замкнутую управляемую подсистему и проверим, что ее полюса совпадают с желаемыми ­ элементами заданного вектора p:

>>Clc=Ac+Bc*Kc;

>>eig(Clc);

Дополним матрицу обратной связи столбцом с нулевыми элементами, соответствующими неуправляемой подсистеме:

>>Kall=[0 Kc(1,:); 0 Kc(2,:)]; % u=Kall*z

>>Clall=A1+B1*Kall;

>>eig(Clall);

Выполним обратную замену переменных, преобразуем матрицу обратных связей и найдем собственные значения замкнутой системы :

>>K=Kall*T;

>>eigcl=eig(A+B*K)

place: ndigits= 15

eigcl =

-1

-1

-2

-2

-1

По построению собственные числа матрицы замкнутой системы составляют набор из элементов вектора p, т.е. четыре собственных числа системы равны соответственно -1 -1 -2 -2, и еще одно собственное число – полюс неуправляемой подсистемы ­ -1. Таким образом, после подстановки управления в исходную систему, она стала асимптотически устойчивой. Аналогичным образом можно построить коэффициенты обратной связи для другого набора собственных значений замкнутой системы, тем самым изменив характеристики решений замкнутой системы.

Сформируем также матрицы обратных связей для наборов заданных собственных чисел управляемой подсистемы p1=[-2;-2; -3; -3] и p2=[-5;-5; -10;-10]:

>>p1=[-2;-2; -3; -3];

>>Kc1=place(Ac,Bc,p1);

>>Kc1=-Kc1;

>>Kall1=[0 Kc1(1,:); 0 Kc1(2,:)];

>>Clall1=A1+B1*Kall1;

>>eig(Clall1); % -1 -2 -2 -3 -3

>>K1=Kall1*T;

>>eigcl1=eig(A+B*K1)

place: ndigits= 15

eigcl1 =

-2.0000

-3.0000

-2.0000

-3.0000

-1.0000

>>p2=[-5;-5; -10; -10];

>>Kc2=place(Ac,Bc,p2);

>>Kc2=-Kc2;

>>Kall2=[0 Kc2(1,:); 0 Kc2(2,:)];

>>Clall2=A1+B1*Kall2;

>>eig(Clall2); % -1 -5 -5 -10 -10

>>K2=Kall2*T;

>>eigcl2=eig(A+B*K2)

place: ndigits= 15

eigcl2 =

-5.0000

-10.0000

-10.0000

-5.0000

-1.0000

Воспользуемся системой Simulink для формирования рассмотренной LTI-модели и трех вариантов управляющих воздействий в виде линейной обратной связи, а также имитационного моделирования динамики в замкнутой системе управления.

Как известно, система Simulink является частью пакета Matlab, предназначенной для проведения имитационного моделирования динамических процессов для математических моделей объектов различной природы. Результаты моделирования формируются в рабочем пространстве среды Matlab и могут быть доступны для дальнейшего исследования свойств функционирования модели объекта.

В системе Simulink содержится большое количество блоков, которые позволяют формировать модель объекта, дополнять её и производить над ней различные действия.

На рис. 4.2.1 приводится Simulink-модель, формирующая динамику замкнутой системы. Модель включает в себя (рис. 4.2.2) блок формирования линейной модели объекта управления (State-Space), входом этого блока является вектор управлений , а выходом ­ вектор , в качестве вектора начальных данных возьмем вектор (например), блок (рис. 4.2.3), содержащий матрицу коэффициентов усиления (Matrix Gain) ­ в нашем случае матрицу коэффициентов матрицы в управлении. Входы и выходы указанных блоков соединены между собой и образуют замкнутую систему . Кроме того, модель содержит блоки вывода результатов моделирования (Scope) в виде графиков функций компонент векторов и .

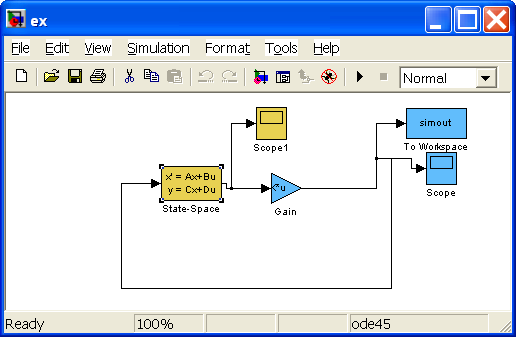
Рис. 4.2.1. Simulink-модель

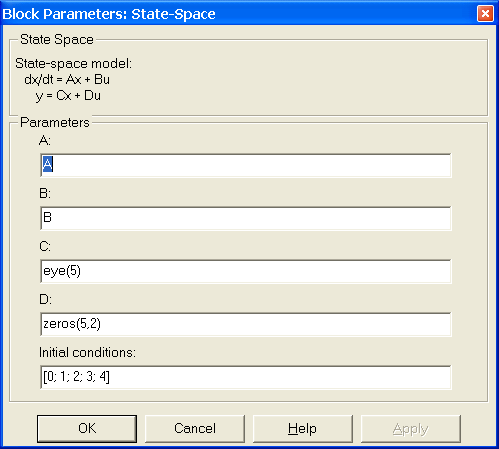
Рис. 4.2.2. Блок формирования модели, заданной в пространстве состояний четверкой матриц {A, B, C, D}

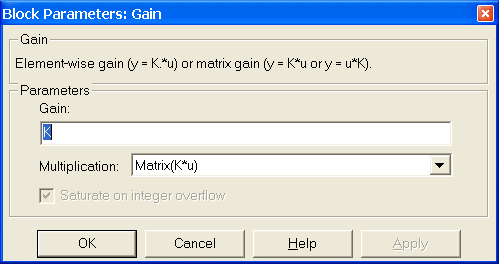
Рис. 4.2.3. Блок, содержащий коэффициенты усиления

Запуск начала моделирования осуществляется либо из командного окна с помощью команды sim('ex'), либо из меню окна модели Simulation->Start, там же задаются параметры моделирования, в частности метод численного интегрирования линейной системы.

На рис. 4.2.4, рис. 4.2.5, рис. 4.2.6 приводятся графики функций компонент вектора , которые отображаются при помощи блока Scope1 соответственно для векторов заданных собственных значений p, p1, и p2 при последовательном осуществлении моделирования для матриц коэффициентов в управлении , и .

На рисунках видно, что во всех рассмотренных вариантах все компоненты решения, порождаемого ненулевыми начальными условиями , стремятся к нулю, однако динамика системы изменяется в зависимости от выбора управляющего воздействия, в том числе уменьшается время переходного процесса, т.е. попадания компонент вектора выхода в заданную достаточно малую окрестность нуля.

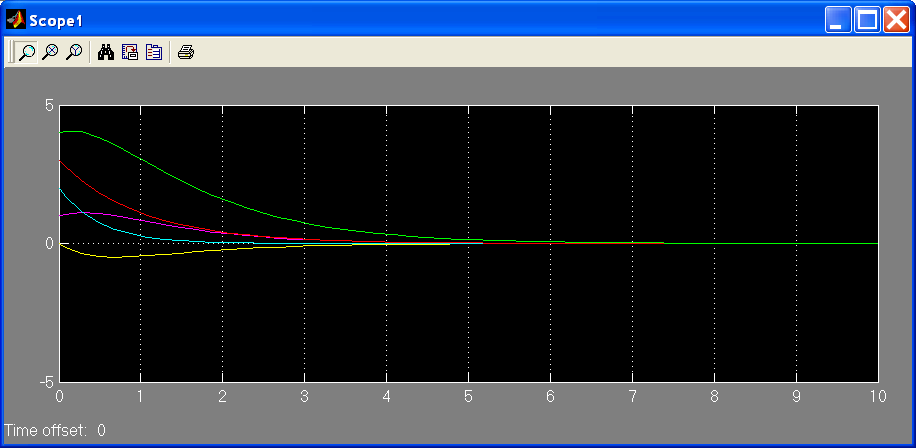
Рис. 4.2.4. Графики компонент вектора выхода для управления

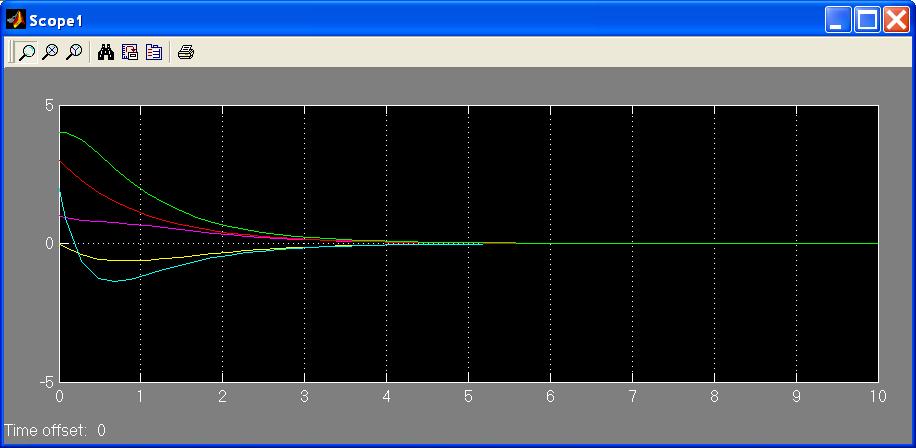
Рис. 4.2.5. Графики компонент вектора выхода для управления

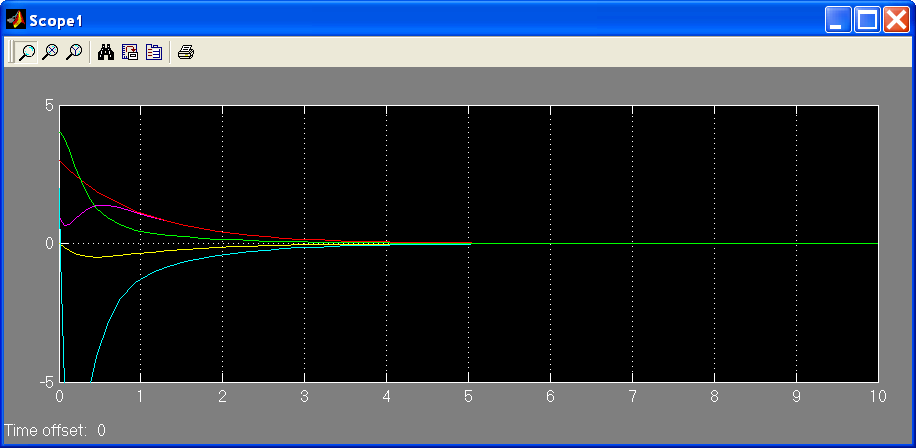
Рис. 4.2.6. Графики компонент вектора выхода для управления