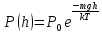Раздел 3. Основы статистического описания термодинамических систем
3.1 Основные понятия. Микро- и макропараметры состояния. Равновесные состояния системы. Понятие фазового пространства и его свойства.
Введем некоторые основные понятия (некоторые из них могут повторяться с тем, что уже было раньше, но большей частью это либо новые, либо углубленные понятия).
Термодинамическая система – это любая система (то есть любое тело), состоящая из множества частиц (то есть макротело).
Существуют параметры, характеризующие эту термодинамическую систему:
- микропараметры (величины, которые характеризующие состояние элементов системы)
- макропараметры (характеризуют состояние всей системы или ее частей)
К примерам первых можно отнести скорость одной молекулы, а вторых – массу системы, давление, температура.
Для описания замкнутости или незамкнутости используются так называемые внешние и внутренние параметры.
Цель и применение статистического метода:
в случае статистического метода не используются параметры отдельных частиц, ищутся общие закономерности для всех частиц сразу, микропараметры не нужны сами по себе, их используют только для нахождения распределений микропараметров по их значениям. Целью статистического метода является нахождение общих закономерностей при помощи знаний законов физики и микропараметров.
 Теперь
перейдем к определению того, что есть
распределение в статистической физике.
Но для начала рассмотрим следующие
рассуждения.
Теперь
перейдем к определению того, что есть
распределение в статистической физике.
Но для начала рассмотрим следующие
рассуждения.
Мы
можем измерить в термодинамической
системе относительное число частиц с
определенной энергией (энергией, входящий
в определенный отрезок) – получится
гистограмма определенного вида (смотри
рисунок). Эта операция вычисления
относительного числа частиц с определенной
энергией повторяется много раз. Тогда
получаемая гистограмма будет колебаться
около одного (наивероятнейшего) значения
– некоторой кривой. Тогда будет возможно
найти
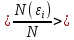 - средние значения, которые будут
устойчивыми. Таким образом, мы будем
находить определенное распределение.
- средние значения, которые будут
устойчивыми. Таким образом, мы будем
находить определенное распределение.
Среди всевозможных распределений существует такое распределение, которое реализуется наибольшим числом микросостояний элементов системы. Это распределение и является наиболее вероятным, равновесным.
Равновесное состояние – это такое состояние системы, которое характеризуется наибольшим числом микросостояний. В таком случае говорят, что система находится в равновесии.
Например,
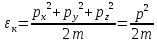 .
Если выбрать определенный интервал, то
найдутся разные
частицы, дающие одинаковое значение
энергии.
.
Если выбрать определенный интервал, то
найдутся разные
частицы, дающие одинаковое значение
энергии.
Более того, само значение энергии, если абстрагироваться от обычных систем координат, можно воспринимать само как координату. Строго говоря координатами (то есть состояниями) в системе может являться все, что угодно. Поэтому возникает понятие фазового пространства.
Фазовое пространство – это пространство, координатами которого являются микропараметры термодинамической системы.
Если
какая-то величина
 может принимать какие-то значения от
может принимать какие-то значения от
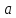 до
до
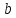 ,
то тогда можно представить одномерное
фазовое пространство. Причем точные
знания параметров не нужны, достаточно
просто разбить ось на небольшие отрезки
,
то тогда можно представить одномерное
фазовое пространство. Причем точные
знания параметров не нужны, достаточно
просто разбить ось на небольшие отрезки
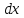 – достаточно малые значения, причем
именно
– достаточно малые значения, причем
именно
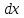 – будет являться элементом фазового
пространства, иначе говоря – объем
фазового пространства.
– будет являться элементом фазового
пространства, иначе говоря – объем
фазового пространства.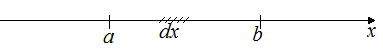
Также
можно представить двумерное фазовое
пространство. В таком случае у нас
имеется величина
 и объемом фазового пространства будет
являться
и объемом фазового пространства будет
являться

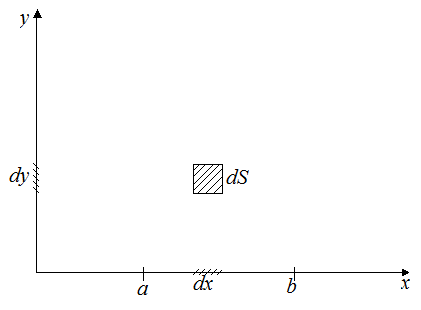
Аналогично – и для пространств с большей размерностью. Для объема фазового пространства характерно перемножение объемов фазовых пространств меньших размерностей.
Свойство мультиплексности: объемы умножаются.
Перейдем теперь к энергетическому состоянию. В этом случае для каждого элемента системы будет 6 независимых координат:

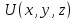
Образуемое
этим шестью координатами фазовое
пространство называется
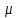 – пространством. Элементом (объемом)
такого пространства будет являться
выражение вида:
– пространством. Элементом (объемом)
такого пространства будет являться
выражение вида:
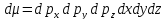
Причем
это пространство можно разбить на два
подпространства,
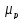 и
и
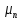 ,
объем которых будет соответственно:
,
объем которых будет соответственно:
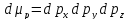 и
и
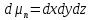 .
.
В конечном итоге мы всегда можем подобрать наиболее удобное для решения определенной задачи фазовое пространство и разбить его именно на те подпространства, которые будут наиболее легки в понимании и расчетах.
Например,
рассмотрим некоторый шар, радиус которого
будет составлять
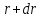 .
Если нам захочется вести некоторые
вычисления в самом примитивном фазовом
пространстве – геометрическом, то в
качестве объема фазового пространства
придется взять элементарный «кубик»,
который будет крайне неудобен при любых
операциях в данной системе. Но если в
качестве объема фазового пространства
взять элементарный объем шарового слоя
толщиной
.
Если нам захочется вести некоторые
вычисления в самом примитивном фазовом
пространстве – геометрическом, то в
качестве объема фазового пространства
придется взять элементарный «кубик»,
который будет крайне неудобен при любых
операциях в данной системе. Но если в
качестве объема фазового пространства
взять элементарный объем шарового слоя
толщиной
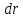 :
:
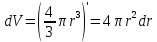 ,
то есть
,
то есть
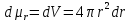 ,
что намного удобнее первоначального
способа. Таким образом, всегда можно
определить наиболее удобное фазовое
пространство.
,
что намного удобнее первоначального
способа. Таким образом, всегда можно
определить наиболее удобное фазовое
пространство.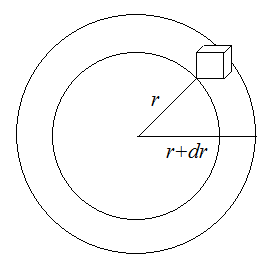
3.2 Элементы теории вероятностей. Случайные величины и их описание. Функция распределения. Средние значения, математическое ожидание, дисперсия и флуктуация. Биномиальное распределение. Распределение в системах с большим количеством элементов. Распределения Пуассона и Гаусса.
Случайное событие – это событие, которое может произойти, а может и не произойти.
Регулярное (достоверное) событие – событие, которое происходит всегда.
Невозможное событие – событие, которое никогда не происходит.
Случайная величина – это количественная величина, характеризующая некоторое случайное событие. Для того, чтобы задать случайную величину, недостаточно просто задать ее значения, необходимо знать вероятность того, что она примет это значение.
Вероятность
определяется как величина
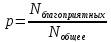 при достаточно больших
при достаточно больших
 .
.
Свойства вероятности:
-

-
Сумма вероятностей:
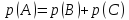 – вероятность того, что произойдет
событие
– вероятность того, что произойдет
событие
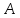 ,
заключающееся в том, что произойдет
либо
,
заключающееся в том, что произойдет
либо
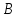 ,
либо
,
либо
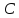 (речь идет о несовместных событиях).
(речь идет о несовместных событиях). -
Произведение вероятностей:
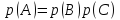 – вероятность того, что произойдет
событие
– вероятность того, что произойдет
событие
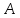 ,
заключающееся в том, что произойдет и
,
заключающееся в том, что произойдет и
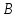 ,
и
,
и
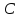 (события совместимы).
(события совместимы). -
Условие нормировки: если случайных событий
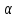 штук и только этим исчерпываются все
значения случайной величины:
штук и только этим исчерпываются все
значения случайной величины:
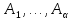 ,
которые случайная величина принимает
с вероятностями
,
которые случайная величина принимает
с вероятностями
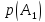 ,
… ,
,
… ,
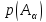 ,
то тогда выполняется условие нормировки:
,
то тогда выполняется условие нормировки:
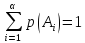
Следствие:
если событие
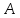 реализуется с вероятностью
реализуется с вероятностью
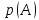 ,
то событие
,
то событие
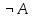 реализуется с вероятностью
реализуется с вероятностью
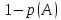 .
.
Среднее значение случайной величины
Пусть
случайная величина
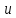 принимается значения
принимается значения
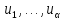 с вероятностями
с вероятностями
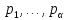 соответственно,
и проводится
соответственно,
и проводится
 опытов, причем значение
опытов, причем значение
 выпало
выпало
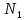 раз, … ,
раз, … ,
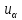 выпало
выпало
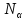 раз. Тогда средним значением случайной
величины
раз. Тогда средним значением случайной
величины
 будет являться величина вида:
будет являться величина вида:
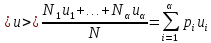
В
том случае если на случайную величину
 будет накладываться некоторая функция
будет накладываться некоторая функция
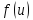 ,
то тогда средняя величина
,
то тогда средняя величина
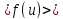 будет считаться следующим образом:
будет считаться следующим образом:
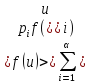
Распределения, плотность распределения
Пусть
функция
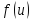 определена на интервале
определена на интервале
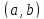 .
Тогда вероятность обнаружить случайную
величину в интервале
.
Тогда вероятность обнаружить случайную
величину в интервале
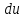 будет равна
будет равна
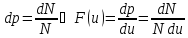 – функция
плотности распределения,
то есть физически – вероятность того,
что случайная величина попадет в
единичный интервал.
– функция
плотности распределения,
то есть физически – вероятность того,
что случайная величина попадет в
единичный интервал.
Тогда
для любой случайной величины (не только
дискретной, но и непрерывной) среднее
значение можно будет найти по формуле:
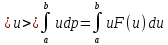
Для
случайной величины
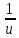 ,
например, среднее значение будет
находиться:
,
например, среднее значение будет
находиться:
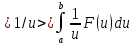
Если найти среднее значение случайной величины на всем интервале, то получится математическое ожидание – среднее средних.
Дисперсия
– это величина, равная
 или иными словами:
или иными словами:
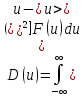
Дисперсия
характеризует вид кривой распределения,
разброс случайной величины по ее
значениям (средний квадрат отклонений
от математического ожидания)
На
рисунке представлены три кривых различных
распределений с разной дисперсией:
 .
Видно, что при одной и той же вероятности
у распределения с большей дисперсией
будет больший разброс по отношению к
математическому ожиданию.
.
Видно, что при одной и той же вероятности
у распределения с большей дисперсией
будет больший разброс по отношению к
математическому ожиданию.
Величина,
равная корню из дисперсии
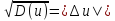 - флуктуация.
- флуктуация.
Рассмотрим некоторые практические задачи.
Задача 1.
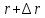
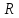 ,
заполненное зернами. Мы хотим узнать
вероятность того, что зерно окажется
на радиусе
,
заполненное зернами. Мы хотим узнать
вероятность того, что зерно окажется
на радиусе
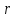 :
:
 функцию распределения зерен по радиусу
функцию распределения зерен по радиусу
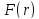 .
.
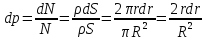
Тогда
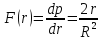
При
этом средний радиус, на котором зерна
окажутся с наибольшей вероятностью (то
есть математическое ожидание) будет
равно
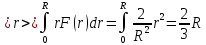
Задача 2.
Рассмотрим
распределения
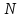 молекул в шарообразном объеме радиуса
молекул в шарообразном объеме радиуса
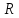 .
.
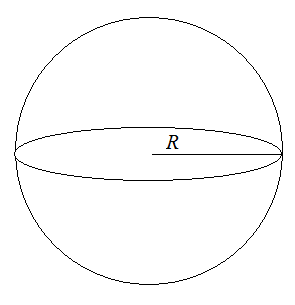
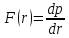
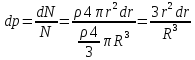
Отсюда
получаем:
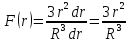
Математическое
ожидание:
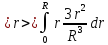
Пример:
пусть дана термодинамическая система,
состоящая из
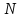 элементов, располагающаяся в физическом
объеме
элементов, располагающаяся в физическом
объеме
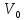 .
Необходимо найти вероятность
.
Необходимо найти вероятность
 того, что в некотором объеме находится
того, что в некотором объеме находится
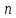 молекул и найти условие равновесия.
молекул и найти условие равновесия.
Пусть
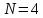
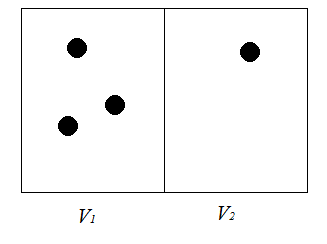
Мы
хотим найти вероятность того, что в
объеме
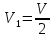 находится
находится
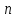 молекул. Если
молекул. Если
 ,
то число реализаций в таком случае
данной ситуации будет равно 1, следовательно,
вероятность будет равна
,
то число реализаций в таком случае
данной ситуации будет равно 1, следовательно,
вероятность будет равна
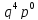 .
При
.
При
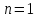 число реализаций – 4 с вероятностью
число реализаций – 4 с вероятностью
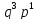 .
При
.
При
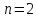 число реализаций – 6 с вероятностью
число реализаций – 6 с вероятностью
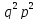 .
И так далее. Таким образом, видно, что
число реализаций составляет число
сочетаний
.
И так далее. Таким образом, видно, что
число реализаций составляет число
сочетаний
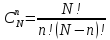
Таким
образом,
 – задает биномиальное
распределение.
– задает биномиальное
распределение.
Наиболее
вероятная ситуация в данном случае –
та ситуация, которая характеризуется
наибольшим числом реализаций, то есть
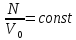 .
Очевидно, что равновесное состояние
системы достигается при равномерном
распределении частиц поровну по двум
половинкам объема
.
Очевидно, что равновесное состояние
системы достигается при равномерном
распределении частиц поровну по двум
половинкам объема
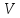 .
.
Данное
условие равновесия можно использовать
для любого
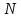 ,
сколь угодно большого.
,
сколь угодно большого.
Распределение Пуассона
Задача:
имеется
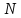 частиц в объеме
частиц в объеме
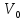 ,
система находится в равновесном
состоянии. Необходимо узнать вероятность
того, что в произвольном объеме
,
система находится в равновесном
состоянии. Необходимо узнать вероятность
того, что в произвольном объеме
 окажется
окажется
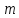 частиц.
частиц.
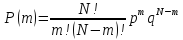
Введем
переменную
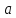 ,
равную:
,
равную:
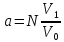 ,
тогда
,
тогда
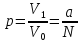
Тогда

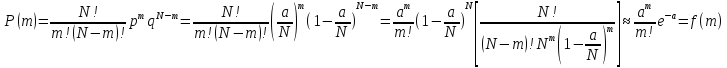
Так задается распределение Пуассона.
Математическое ожидание в распределении Пуассона будет равно:
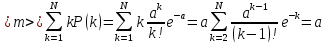 – среднее
число частиц
– среднее
число частиц
Проверить работоспособность распределения Пуассона можно следующим образом:

Очевидно, распределения Пуассона в этом случае работает.
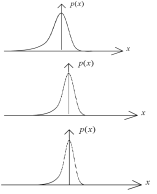 Приведенные
три рисунка показывают кривые распределения
Пуассона при все более возрастающих
объемах
Приведенные
три рисунка показывают кривые распределения
Пуассона при все более возрастающих
объемах
 .
По этим рисункам видно, что распределение
становится все более симметричным и
стремится к некоторому другому
распределению.
.
По этим рисункам видно, что распределение
становится все более симметричным и
стремится к некоторому другому
распределению.
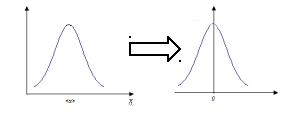
Данное симметричное распределение называется распределением Гаусса или нормальным распределением – оно является симметричным.
Проделаем следующие шаги с распределением Пуассона:
-
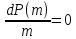 (отклонения
малы)
(отклонения
малы) -
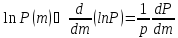
-
Найдем математическое ожидание
 и раскладываем в ряд Тейлора в окрестности
этого математического ожидания
и раскладываем в ряд Тейлора в окрестности
этого математического ожидания -
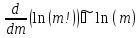
В результате данных шагов получим распределение, характеризующееся следующим соотношением:
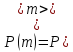
где

Если
произвести нормировку:
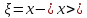 ,
то получится из первого рисунка второй,
причем плотность вероятности примет
вид:
,
то получится из первого рисунка второй,
причем плотность вероятности примет
вид:
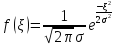
Найдем математическое ожидание в этом случае:
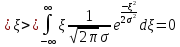
Найдем дисперсию:
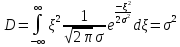
СЛУЧАЙНАЯ ВЕЛИЧИНА, ЗАВИСЯЩАЯ ОТМНОЖЕСТВА НЕЗАВИСИМЫХ НЕДОМИНИРУЮЩИХ ФАКТОРОВ ПОДЧИНЯЕТСЯ ЗАКОНУ ГАУССА.
Причем
если найти вероятность попадания в
интервале
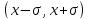 ,
то эта величина будет постоянная для
любого нормального распределения и
равна
,
то эта величина будет постоянная для
любого нормального распределения и
равна
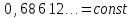
Подсчитаем
среднее отклонение числа молекул в
одном моле газа при нормальных условиях,
то есть атмосферное давление
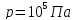 и объеме
и объеме
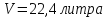 .
Это будет около
.
Это будет около
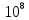 молекул! Несмотря на то, что число
огромно, относительно общего числа
молекул это будет совсем незначительно:
молекул! Несмотря на то, что число
огромно, относительно общего числа
молекул это будет совсем незначительно:
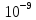 .
.
 Ранее
мы искали длину свободного пробега
молекулы газа при помощи динамического
метода. Теперь покажем, насколько проще
выкладки, если пользоваться статистическим
методом: обозначим число столкновений
Ранее
мы искали длину свободного пробега
молекулы газа при помощи динамического
метода. Теперь покажем, насколько проще
выкладки, если пользоваться статистическим
методом: обозначим число столкновений
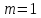 ,
если
,
если
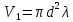 .
.
Тогда
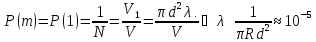
3.3 Статистические распределения для идеального газа. Координата и скорость молекулы как случайные величины. Фазовое пространство координат и импульсов, обобщенные координаты. Функция Гамильтона. Каноническое распределение Гиббса. Распределение молекул по скоростям Масквелла. Закон распределения энергии по степеням свободы. ТДС в поле внешних сил. Идеальный газ в гравитационном поле, распределение Максвелла-Больцмана.
Простейшее
фазовое пространство представляется
как пространство координат и импульсов
–
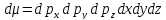 .
Намного более сложной является задача
о отом, чтобы подсчитать зависимость
не от скоростей и положения молекул в
пространстве, а от того, какой энергией
они обладают.
.
Намного более сложной является задача
о отом, чтобы подсчитать зависимость
не от скоростей и положения молекул в
пространстве, а от того, какой энергией
они обладают.
Пусть
нам даны
 частиц и они взаимодействуют только в
момент столкновения, эти частица
находятся в некотором внешнем силовом
поле. Необходимо найти наиболее вероятное
(а следовательно, и равновесное)
распределение этих элементов по энергии
частиц и они взаимодействуют только в
момент столкновения, эти частица
находятся в некотором внешнем силовом
поле. Необходимо найти наиболее вероятное
(а следовательно, и равновесное)
распределение этих элементов по энергии
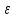 .
.
Представим,
что эта система – идеальный газ. Тогда
из свойств этой математической модели
следует, что
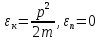
Но
поскольку имеется внешнее силовое поле,
то также речь идет и об потенциальной
энергии внешнего силового поля:
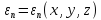
Но вспомним, что сейчас речь шла об идеальном газе – по сути, математической модели. Если же в качестве системы взять реальный газ, например, воздух, то тогда у молекул есть диаметр, возможно вращательное и колебательное движение, потому в фазовое пространство будут добавляться все новые и новые координаты, что неумолимо приведет к перегруженности каких бы то ни было расчетов. Поэтому вводится понятие обобщенных координат – заводится по координате на кинетическую и на потенциальную составляющие энергии как координаты в фазовом пространстве:
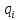 – обобщенная
координата, отвечающая за
– обобщенная
координата, отвечающая за
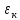
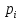 -
обобщенная
координата, отвечающая за
-
обобщенная
координата, отвечающая за
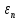
Полная
энергия в таком случае будет искаться
по формуле:
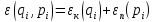
В
этом фазовом пространстве каждая точка
будет являться энергетическим состоянием
одной молекулы. Тогда
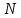 точек будут определять состояние всей
системы. И эти точки будут распределяться
с некоторой плотностью в фазовом
пространстве. Тогда
точек будут определять состояние всей
системы. И эти точки будут распределяться
с некоторой плотностью в фазовом
пространстве. Тогда
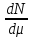 – плотность распределения, где
– плотность распределения, где
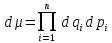 ,
также можно написать:
,
также можно написать:
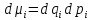
Разумеется,
есть естественное желание свести
плотность к знакомой нам формуле:
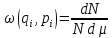 – и сделать функцию плотности распределения
по энергии.
– и сделать функцию плотности распределения
по энергии.
Теорема Лиувилля: если функция распределения в фазовом пространстве является функцией обобщенных координат (а она является), то она зависит только от значений энергии, а не от конкретного значения этих обобщенных координат.
В математическом смысле это означает, что:
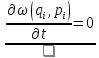
Иначе
говоря:
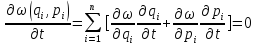
Аксиома Гиббса: если плотность распределения вероятности в фазовом пространстве есть функция обобщенных координат не иначе как через функцию Гамильтона, то тогда:
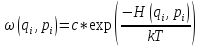
где
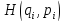 – гамильтониан.
– гамильтониан.
Свойства распределения Гиббса:
-
Нет ограничения на обмен энергии
-
Функция Гамильтона – случайная величина
-
Если ТДС
 может быть представлена в виде двух
подсистем:
может быть представлена в виде двух
подсистем:
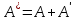 так, что гамильтониан
так, что гамильтониан
 ,
то тогда
,
то тогда
 ,
а если
,
а если
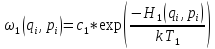 и
и
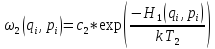 ,
то тогда систему можно разбить на две
подсистемы и рассматривать их в
отдельности.
,
то тогда систему можно разбить на две
подсистемы и рассматривать их в
отдельности.
Теперь рассмотрим подробнее саму функцию Гамильтона.
 Ее
можно найти из системы уравнений:
Ее
можно найти из системы уравнений:
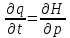
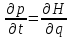
Перейдем теперь к переменным Ньютона:
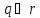 – радиус-вектор
– радиус-вектор
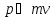 – импульс
– импульс
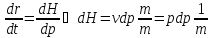 ,
тогда
,
тогда
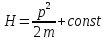
По
второму закону Ньютона
 (так как
(так как
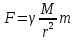 – гравитационная сила)
– гравитационная сила)
 (минус ушел, так как направления
(минус ушел, так как направления
 противоположны)
противоположны)
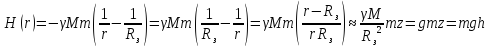
Таким
образом,
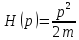 ,
,
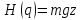
Тогда функция распределения будет выглядеть:
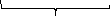
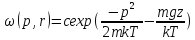 – распределение
Максвелла-Больцмана
– распределение
Максвелла-Больцмана
Две
подсистемы
Найдем
условие равновесия системы
 С гамильтонианом
С гамильтонианом
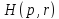 ,
состоящую из двух вышеуказанных
подсистем.
,
состоящую из двух вышеуказанных
подсистем.
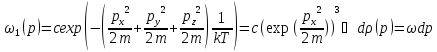
Таким
образом,
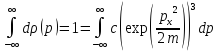
Отсюда

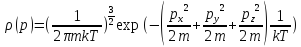
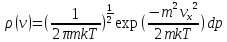
Отсюда
получаем
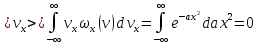
Закон распределения энергии по степеням свободы
Рассмотрим распределение Гаусса:
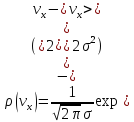
Где
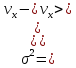
Таким образом, на одну степень свободы приходится энергия, равная:
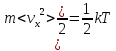
Это
легко проверить: ведь такая энергия
приходится на одну координату,
следовательно, на три координаты будет
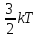 ,
что верно для идеального газа.
,
что верно для идеального газа.
Таким образом, энергия системы равномерно распределяется по всем степеням свободы.
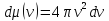
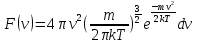

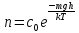
– концентрация молекул около поверхности Земли
Если
домножить на
 ,
то получим аналогичное соотношения для
давления:
,
то получим аналогичное соотношения для
давления: