Тема 2.4.Геометрические характеристики сечений Полярный и осевые моменты инерции

В дальнейшем в расчетах на прочность мы будем встречаться еще с некоторыми геометрическими характеристиками сечений. Это так называемые моменты инерции сечений. Различают полярные и осевые моменты инерции.

Полярным моментом инерции сечения называется взятая по всему сечению сумма произведений или интеграл элементарных площадей на квадраты их расстояний до некоторой точки О сечения.

J_p =

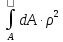
Для поперечных сечений в форме круга или кругового кольца полярный момент инерции характеризует способность сопротивляться кручению и используется как геометрическая характеристика поперечного сечения при расчетах на кручение. Полярный момент инерции измеряется в единицах длины в четвертой степени (см⁴, мм⁴, м⁴).

Практический интерес представляет полярный момент инерции относительно центра тяжести сечения.

Величина полярного момента инерции круга определяется по следующей формуле J_р = πd⁴/32,

или приближенно J_р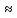0,1 d⁴

Полярный момент инерции кольца равен разности полярных моментов инерции двух кругов диаметрами d_н и d_в

J_р = (πd⁴ _н/32)(1-α⁴) , где α= d_в / d_н

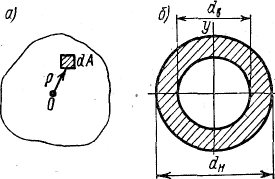
Приближенно для кольца J_р = 0,1d⁴(1— α⁴)

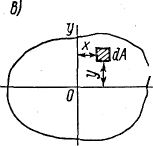
Осевым моментом инерции сечения называется взятая по всему сечению сумма произведений или интеграл элементарных площадок на квадраты их расстояний до некоторой оси, лежащей в пло­скости рассматриваемого сечения.

Так, относительно осей х и у (рис.в) осевые моменты инерции определяются следующими выражениями: J_x =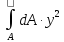; J_y =.

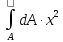Величина осевого момента инерции служит характеристикой способности балки сопротивляться изгибу. Осевые моменты инер­ции, так же как полярные, всегда положительны и измеряются в единицах длины в четвертой степени (см⁴, мм⁴, м⁴).

В практических расчетах наибольший интерес представляют моменты инерции относительно так называемых главных осей, проходящих через центр тяжести сечения. В дальнейшем будем рассматривать только сечения, имеющие не менее одной оси сим­метрии.

Относительно одной из главных центральных осей момент инерции имеет наибольшее из всех возможных значений, а отно­сительно другой — наименьшее. Ось симметрии сечения всегда является одной из главных центральных осей, а другая главная центральная ось ей перпендикулярна. В дальнейшем рассматри­ваются сечения, обладающие симметрией, что позволяет легко определять их главные центральные оси.

Для прямоугольного сечения (рис. а) осевой момент инер­ции определяется по формуле: J_x =bh³/12.

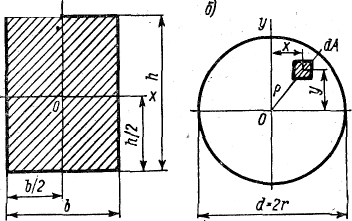
Для круга моменты инерции относительно любых осей, про­ходящих через его центр, равны между собой, т.е. J_x = J_y поэтому

J_x = J_y= = πd⁴/6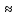40,05 d⁴

Аналогично для кольцевого сечения J_x = J_y = (πd⁴ _н/54)(1-α⁴)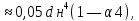 где α= d_в / d_н

Осевые моменты инерции относительно параллельных осей

Для вычисления осевых моментов инерции сложных сечений часто приходится пользоваться теоремой о моментах инерции относительно параллельных осей.

Момент инерции сечения отно­сительно оси, не проходящей через его центр тяжести, равен сумме момента инерции сечения относительно его центральной оси, параллельной данной оси, и произведения площади сечения на квадрат расстояния между осями.

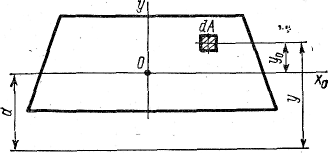
Обозначим у расстояние элементарной площадки а от оси х, а yо — расстоя­ние от параллельной ей центральной оси х₀; расстоя­ние между осями обозначим aочевидно,

что у= yо + а.

Момент инерции рассматриваемого сечения относительно оси х

J_x = J_x0+Aa².