
- •§6 Линейные дифференциальные уравнения второго порядка
- •6.1. Общие понятия
- •§6. Линейные однородные уравнения с постоянными коэффициентами.
- •Примеры для самостоятельной работы.
- •§7 Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- •7.1.Метод вариации произвольных постоянных (метод Лагранжа) решения лнду.
- •7.2. Метод подбора частного решения лнду по виду правой части (метод неопределенных коэффициентов).
- •7.3. Структура частного решения лнду с аддитивной правой частью.
7.2. Метод подбора частного решения лнду по виду правой части (метод неопределенных коэффициентов).
Этот метод
применим к решению ЛНДУ
с постоянными коэффициентами вида (3)
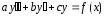 только в случаях, когда его правая часть
:
только в случаях, когда его правая часть
:
-
многочлен;
-
показательная функция;
-
тригонометрические функции
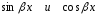 (или одна
из них);
(или одна
из них); -
линейная комбинация перечисленных функций;
-
произведение перечисленных функций.
Таким образом, рассматриваемый метод применяется при следующем виде правой части ЛНДУ:
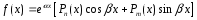 ,
(2)
,
(2)
где
 -
многочлен степени
-
многочлен степени
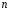 ,
а
,
а
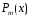 -
многочлен степени
-
многочлен степени
 ,
,
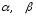 -заданные
числа. Возможны разновидности этого
вида правой части в зависимости от
того, содержатся или нет в
-заданные
числа. Возможны разновидности этого
вида правой части в зависимости от
того, содержатся или нет в
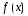 тригонометрические функции.
тригонометрические функции.
Сущность метода состоит в том , что :
-
по характерному виду правой части ЛНДУ
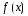 и корням характеристического уравнения
соответствующего ЛОДУ
определяется
общий вид
частного
решения
и корням характеристического уравнения
соответствующего ЛОДУ
определяется
общий вид
частного
решения
 уравнения (ниже рассматриваются
различные случаи
уравнения (ниже рассматриваются
различные случаи
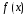 и соответствующих им
и соответствующих им
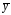 );
);
-
неизвестные коэффициенты многочлена или тригонометрических функций в искомом
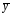 находятся методом
неопределенных коэффициентов.
Он состоит в приравнивании коэффициентов
при одинаковых степенях
находятся методом
неопределенных коэффициентов.
Он состоит в приравнивании коэффициентов
при одинаковых степенях
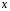 ( или при одноимённых тригонометрических
функциях) левой и правой частей
уравнения, полученного в результате
подстановки в данное
ЛНДУ частного
решения
( или при одноимённых тригонометрических
функциях) левой и правой частей
уравнения, полученного в результате
подстановки в данное
ЛНДУ частного
решения
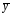 ( в его общем виде) и его производных
( в его общем виде) и его производных
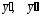 ;
; -
найденные коэффициенты подставляются в предварительно установленный общий вид
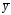 ,
в результате находится
,
в результате находится
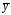 .
. -
далее в соответствии со структурой общего решения ЛНДУ суммируется
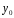 ЛОДУ
и
ЛОДУ
и
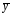 ЛНДУ
и получается
ЛНДУ
и получается
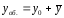 .
.
Рассмотрим
два различных вида ( и их частные случаи)
правой части
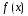 ЛНДУ (3)
и соответствующие им виды частного
решения
ЛНДУ (3)
и соответствующие им виды частного
решения
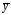 (см.
таблицу 3).
(см.
таблицу 3).
Таблица 3.
Частное решение линейных неоднородных дифференциальных уравнений по виду его правой части
|
|
Вид правой части и его частные случаи |
Вид
частного решения
|
|
I |
|
Примеры
многочленов
|
|
|
Случай 1.
|
|
|
|
Случай 2.
|
|
|
II |
где
|
|
|
|
Случай
1.
т.е.
степени, т.е.
постоянные числа,
|
|
|
|
Случай
2.
|
|
Рассмотрим сущность метода подбора частного решения ЛНДУ по виду правой части на примерах.
I вид. Правая часть ЛНДУ
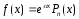 ,
(1)
,
(1)
где
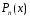 -
многочлен
-
многочлен
 -ой
степени,
-ой
степени,
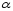 -
постоянное число. Тогда общий вид
частного решения:
-
постоянное число. Тогда общий вид
частного решения:
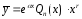 ,
где
,
где
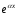 -
та же самая показательная функция, что
и в
-
та же самая показательная функция, что
и в
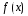 ;
;
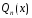 -
многочлен той же степени, что и
-
многочлен той же степени, что и
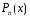 ;
;
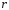 -
число корней характеристического
уравнения, равных
-
число корней характеристического
уравнения, равных
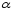 .
.
Далее путем
подстановки общего вида
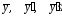 в линейное неоднородное дифференциальное
уравнение находятся неопределённые
коэффициенты многочлена
в линейное неоднородное дифференциальное
уравнение находятся неопределённые
коэффициенты многочлена
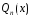 .
.
Пример 3. Найти общее решение дифференциального уравнения:
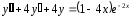 .
.
Решение.
-
Находим общее решение
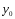 соответствующего линейного однородного
дифференциального уравнения:
соответствующего линейного однородного
дифференциального уравнения:
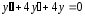 .
.
Характеристическое
уравнение :
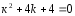 .
Его корни
.
Его корни
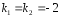 .
Общее решение ЛОДУ:
.
Общее решение ЛОДУ:
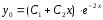 .
.
-
Правая часть
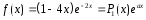 .
Следовательно, общий вид частного
решения ЛНДУ:
.
Следовательно, общий вид частного
решения ЛНДУ:
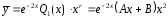 ,
(
,
(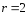 ,
т.к. оба корня характеристического
уравнения совпадают с
,
т.к. оба корня характеристического
уравнения совпадают с
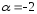 ).
Итак,
).
Итак,
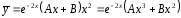 .
.
-
Найдем неизвестные коэффициенты А и В. Для этого подставим в данное дифференциальное уравнение
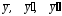 .
Предварительно найдем их, а затем
умножим соответственно на 4, 4 и 1:
.
Предварительно найдем их, а затем
умножим соответственно на 4, 4 и 1:

Сложим левые и
правые части этих равенств, получим
алгебраическое уравнение с тремя
неизвестными
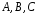 .
Разделим обе части полученного уравнения
на
.
Разделим обе части полученного уравнения
на
 .
Приравниваем коэффициенты слева и
справа при одинаковых степенях
.
Приравниваем коэффициенты слева и
справа при одинаковых степенях
 :
:
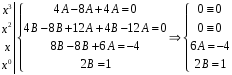
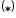
Решение системы:
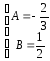 .
.
-
Подставим A и B в общий вид
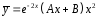 ,
получим
,
получим
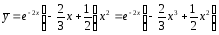 .
.
-
Найдем общее решение ЛНДУ:
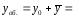
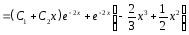 .
.
Ответ:
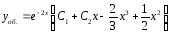 .
.
Замечание. Следует обратить внимание на то, что полученное в данном примере значение r=2 (кратность корней) привело к двум не информативным алгебраическим уравнениям (*).
В практике решения ЛНДУ распространены следующие частные случаи I-го вида правой части f(x).
Случай 1.
Правая часть
ЛНДУ:
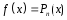 ,
где
,
где
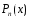 - многочлен n-ой
степени, т.е.
- многочлен n-ой
степени, т.е.
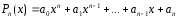 .
.
Таким образом, в
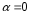 .
.
Тогда общий вид
частного решения:
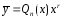 ,
где
,
где
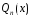 -
многочлен той же степени, что и
-
многочлен той же степени, что и
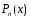 ,
r
– число корней характеристического
уравнения, равных нулю.
,
r
– число корней характеристического
уравнения, равных нулю.
Далее, дифференцируя
функцию
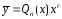 и подставляя выражения
и подставляя выражения
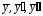 в ЛНДУ,
находим неопределенные коэффициенты
многочлена
в ЛНДУ,
находим неопределенные коэффициенты
многочлена
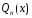 .
.
Подставляя эти
коэффициенты в общий вид
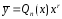 ,
находим частное решение ЛНДУ.
,
находим частное решение ЛНДУ.
Напомним общий вид многочленов:
-
третьей степени (n=3):
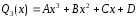 ;
; -
второй степени (n=2):
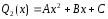 ;
; -
первой степени (n=1):
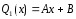 ;
; -
нулевой степени (n=0):
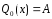 .
.
Пример 4. Найти общее решение ДУ:
 .
.
Решение.
-
Находим общее решение
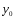 соответствующего
ЛОДУ:
соответствующего
ЛОДУ:
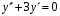 .
.
Характеристическое
уравнение:
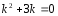 .
Его корни:
.
Его корни:
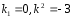 .
.
Общее решение
ЛОДУ:
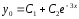 .
.
-
Правая часть
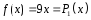 ,
следовательно общий вид частного
решения ЛНДУ:
,
следовательно общий вид частного
решения ЛНДУ:
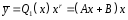 ,
,
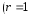 ,
т.к. один корень характеристического
уравнения равен 0).
,
т.к. один корень характеристического
уравнения равен 0). -
Найдем неизвестные коэффициенты A и B. Для этого подставим в данное ДУ
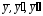 :
:
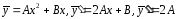 .
.
Тогда
 .
.
Приравниваем
коэффициенты при одинаковых степенях
 :
:
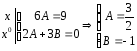 .
.
-
Подставим A и B в общий вид
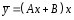 ,
получим
,
получим
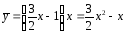 .
.
-
Найдем общее решение ЛНДУ:
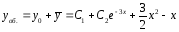 .
.
:
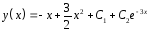 .
.
Ответ:
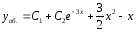 .
.
Случай 2.
Правая
часть ЛНДУ:
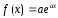 ,
где
,
где
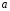 - постоянное число, т.е. в (20)
- постоянное число, т.е. в (20)
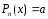 - многочлен нулевой степени (
- многочлен нулевой степени (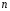 =0).
=0).
Тогда общий вид
частного решения:
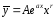 ,
где
,
где
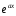 - та же показательная функция;
- та же показательная функция;
 - постоянное число (в общем случае
- постоянное число (в общем случае
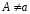 ),
которое находится методом неопределенных
коэффициентов;
),
которое находится методом неопределенных
коэффициентов;
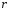 - число корней характеристического
уравнения, равных
- число корней характеристического
уравнения, равных
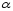 .
.
Возможен и еще
один, наиболее простой, частный случай
(вернее, подслучай) вида правой части
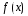 ЛНДУ:
ЛНДУ:
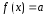 ,
т.е. в (20)
,
т.е. в (20)
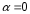 ,
,
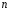 =0.
Тогда общий вид частного решения:
=0.
Тогда общий вид частного решения:
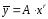 ,
где
,
где
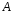 - постоянное число, которое находится
методом неопределенных коэффициентов,
- постоянное число, которое находится
методом неопределенных коэффициентов,
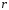 - число корней характеристического
уравнения, равных нулю. Рассмотрим
второй вид
правой части
- число корней характеристического
уравнения, равных нулю. Рассмотрим
второй вид
правой части
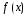 ЛНДУ,
в котором содержатся тригонометрические
функции
ЛНДУ,
в котором содержатся тригонометрические
функции
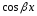 и
и
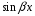 ,
т.е. наиболее общий вид (19) и его частные
случаи.
,
т.е. наиболее общий вид (19) и его частные
случаи.
II
вид. Правая
часть ЛНДУ
содержит тригонометрические функции
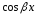 и
и
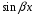 ,
с полными многочленами перед ними:
,
с полными многочленами перед ними:
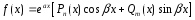 ,
(19)
,
(19)
где
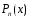 - многочлен
- многочлен
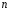 -ой
степени,
-ой
степени,
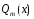 - многочлен
- многочлен
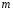 -ой
степени.
-ой
степени.
Тогда общий вид частного решения:
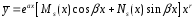 ,
,
где
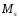 и
и
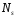 - многочлены
- многочлены
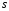 -ой
степени,
-ой
степени,
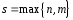 ;
;
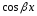 и
и
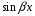 - те же тригонометрические функции, что
и в правой части
- те же тригонометрические функции, что
и в правой части
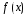 ДУ;
ДУ;
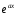 - та же показательная функция;
- та же показательная функция;
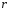 - число корней характеристического
уравнения, совпадающих с
- число корней характеристического
уравнения, совпадающих с
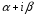 .
Далее применяется метод неопределенных
коэффициентов.
.
Далее применяется метод неопределенных
коэффициентов.
Пример 5. Найти общее решение ДУ:
 .
.
Решение.
-
Находим общее решение
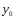 соответствующего
ЛОДУ:
соответствующего
ЛОДУ:
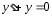 .
.
Характеристическое
уравнение
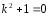 .
Его корни комплексные
.
Его корни комплексные
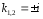 .
Общее решение ЛОДУ:
.
Общее решение ЛОДУ:
 .
.
-
Правая часть
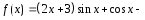 соответствует общему виду (19), когда
многочлены
при
соответствует общему виду (19), когда
многочлены
при
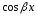 и
и
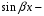 полные.
В данном случае:
полные.
В данном случае:
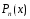 =1
– многочлен 0-ой степени,
=1
– многочлен 0-ой степени,
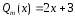 –
многочлен 1-й
степени,
–
многочлен 1-й
степени,
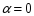 ,
т.к. множитель
,
т.к. множитель
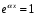 (поэтому
в записи
(поэтому
в записи
 он отсутствует).
он отсутствует).
Тогда этому виду правой части соответствует частное решение вида
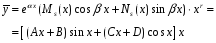 ,
,
т.к.
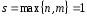 ,
т.е. при
,
т.е. при
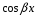 и
и
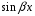
 многочлены
1-й степени,
многочлены
1-й степени,
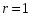 (т.к.
(т.к.
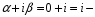 совпадает с корнем характеристического
уравнения).
совпадает с корнем характеристического
уравнения).
-
Найдем неизвестные коэффициенты A, B, C, D.
Для этого подставим
в данное ДУ
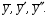 Предварительно найдем их, а затем
умножим соответственно на 1, 0, 1:
Предварительно найдем их, а затем
умножим соответственно на 1, 0, 1:
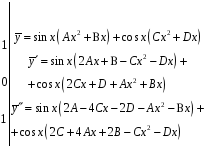 .
.
Сложив соответственно левые и правые части этих равенств, получим алгебраическое уравнение с неизвестными А, В, С, D.
Аналогично предыдущим примерам приравниваем коэффициенты при одинаковых функциях соответственно левой и правой частей уравнения:
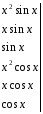
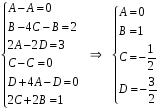
-
Подставим А, B, C, D в общий вид
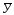 :
:
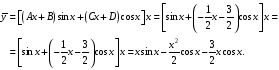
-
Найдем общее решение ЛНДУ:
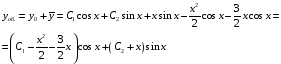
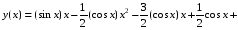
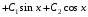 .
.
Ответ:
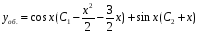 .
.
В практике решения
ЛНДУ
распространены следующие частные
случаи II-го
вида правой части
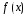 .
.
Случай 1. Правая часть ЛНДУ:
 ,
,
где
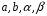 -
известные действительные числа. Таким
образом, в (19)
-
известные действительные числа. Таким
образом, в (19)
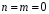 ,
т.е.
,
т.е.
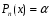 и
и
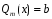 -
многочлены 0-ой степени.
-
многочлены 0-ой степени.
Тогда общий вид частного решения:
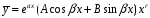 ,
,
где
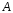 и
и
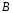 -
неизвестные действительные числа,
которые находятся методом неопределенных
коэффициентов;
-
неизвестные действительные числа,
которые находятся методом неопределенных
коэффициентов;
 и
и
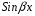 -
те же тригонометрические функции, что
и в
-
те же тригонометрические функции, что
и в
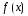 ;
;
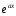 -
та же показательная функция;
-
та же показательная функция;
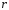 -
число корней характеристического
уравнения, совпадающих с
-
число корней характеристического
уравнения, совпадающих с
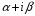 .
.
Пример 6. Найти общее решение ДУ:
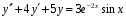 .
.
Решение.
-
Находим общее решение
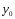 соответствующего ЛОДУ:
соответствующего ЛОДУ:
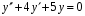 .
.
Характеристическое
уравнение:
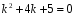 .
Его корни комплексные:
.
Его корни комплексные:
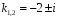 .
.
Общее решение
ЛОДУ:
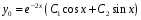 .
.
-
Правая часть соответствует первому частному случаю II вида правой части:
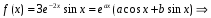
 .
.
(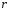 =1,
т.к.
=1,
т.к.
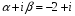 совпадает с корнем характеристического
уравнения).
совпадает с корнем характеристического
уравнения).
-
Найдем неизвестные коэффициенты
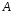 и
и
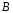 .
Для этого предоставим данное ДУ
.
Для этого предоставим данное ДУ
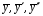 .
Предварительно найдем их, а затем
умножим соответственно на 5,4 и 1:
.
Предварительно найдем их, а затем
умножим соответственно на 5,4 и 1:
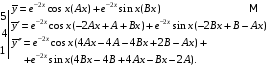
Сложим соответственно
левые и правые части этих равенств,
получим алгебраическое уравнение с
двумя неизвестными
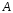 и
и
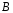 .
.
Разделим обе части
полученного уравнения на
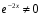 .
Аналогично предыдущему примеру,
приравниваем коэффициенты при одинаковых
функциях соответственно левой и правой
частей уравнения:
.
Аналогично предыдущему примеру,
приравниваем коэффициенты при одинаковых
функциях соответственно левой и правой
частей уравнения:
 (*)
(*)
Вновь (как это было в примере 3) два уравнения с неизвестными коэффициентами в (*) не информативны. Из оставшихся уравнений имеем:
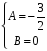 .
.
-
Подставим
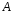 и
и
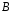 в общий вид
в общий вид
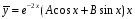 ,
получим
,
получим
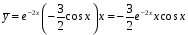 .
.
-
Найдем общее решение ЛНДУ:
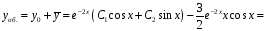
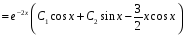 .
.
Ответ:
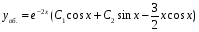 .
.
Случай 2. Правая часть ЛНДУ:
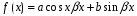 ,
,
где
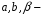 известные
действительные числа. Таким образом,
в (19) многочлены 0-ой степени, т.е.
известные
действительные числа. Таким образом,
в (19) многочлены 0-ой степени, т.е.
 .
.
Тогда общий вид частного решения:
 ,
,
где
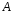 и
и
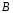 -
неизвестные действительные числа,
которые находятся методом неопределенных
коэффициентов;
-
неизвестные действительные числа,
которые находятся методом неопределенных
коэффициентов;
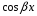 и
и
 -
те же тригонометрические функции, что
и в
-
те же тригонометрические функции, что
и в
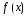 ;
;
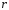 -
число корней характеристического
уравнения, совпадающих с
-
число корней характеристического
уравнения, совпадающих с
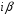 .
.
Пример7. Определить общий вид частного решения ДУ
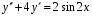 .
.
Решение.
-
Составим характеристическое уравнение соответствующего ЛНДУ:
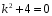 .
Его корни
.
Его корни
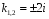 .
. -
Правая часть
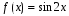 соответствует второму частному случаю
II
вида, следовательно
соответствует второму частному случаю
II
вида, следовательно
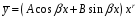 ,
,
где

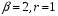 (т.к.
(т.к.
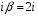 -
совпадает с одним корнем характеристического
уравнения).
-
совпадает с одним корнем характеристического
уравнения).
Таким образом,
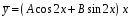 -
общий вид частного решения.
-
общий вид частного решения.
Ответ:
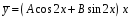 -
общий вид частного решения.
-
общий вид частного решения.
Обобщением всех
рассмотренных случаев правой части
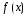 при нахождении частного решения
при нахождении частного решения
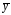 ЛНДУ
является (19) (в таблице 3 вида II)
ЛНДУ
является (19) (в таблице 3 вида II)
Завершая рассмотрение решения ЛНДУ методом неопределенных коэффициентов, представим общую схему (Рис.1)
|
1-й этап
|
|
2-й
этап
|
|
что найти
|
ЛОДУ |
ЛНДУ |
|
как найти |
(см. табл.2).
|
в
|
|
3-й этап
|
Найти
общее решение ЛНДУ |
|
Рис. 1 Общая схема решения ЛНДУ методом неопределенных коэффициентов

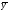
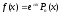 ,
где
,
где
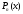 -многочлен
-многочлен
 -ой
степени;
-ой
степени; -постоянное
число.
-постоянное
число.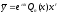 ,
где
,
где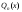 -
многочлен той же степени, что и
-
многочлен той же степени, что и
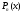 ;
; -
та же показательная функция;
-
та же показательная функция; -
число корней характеристического
уравнения, равных
-
число корней характеристического
уравнения, равных
 ,
т.е.
,
т.е.

 разных степеней:
разных степеней: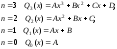
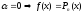
 ,
где:
,
где: -
число корней характеристического
уравнения, равных
-
число корней характеристического
уравнения, равных
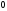 ;
;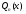 -
многочлен той же степени, что и
-
многочлен той же степени, что и
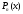 ;
;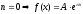 где
где постоянное число(многочлен 0-ой
степени).
постоянное число(многочлен 0-ой
степени).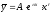 ,
где
,
где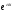 -
та же показательная функция;
-
та же показательная функция; -
число корней характеристического
уравнения, равных
-
число корней характеристического
уравнения, равных
 .
.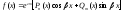
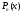 - многочлен степени
- многочлен степени
 ,
а
,
а
 -
многочлен степени
-
многочлен степени
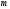 ,
,
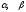 -заданные числа.
-заданные числа.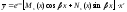 ,
где:
,
где: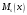 и
и
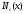 -
многочлены степени
-
многочлены степени
 ,
(где
,
(где
 ).
).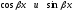 -
те же самые тригонометрические
функции, что и в
-
те же самые тригонометрические
функции, что и в
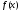 ;
;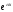 -
та же показательная функция;
-
та же показательная функция; -
число корней характеристического
уравнения, совпадающих с
-
число корней характеристического
уравнения, совпадающих с
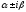 ,
т.е.
,
т.е.

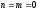 ,
,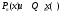 -
многочлены 0-й
-
многочлены 0-й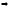
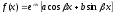 ,
где
,
где
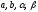 - действительные числа ( в частности,
возможно
- действительные числа ( в частности,
возможно
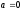 или
или
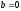 ).
).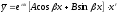 ,
где
,
где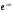 -
та же показательная функция;
-
та же показательная функция;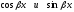 -
те же самые тригонометрические
функции, что и в
-
те же самые тригонометрические
функции, что и в
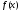 ;
; -
число корней характеристического
уравнения, совпадающих с
-
число корней характеристического
уравнения, совпадающих с
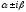 .
.
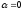 ,
,
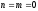 ,
,
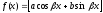 ,
где
,
где
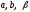 - действительные числа .
- действительные числа .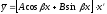 ,
где
,
где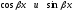 -
те же самые тригонометрические
функции, что и в
-
те же самые тригонометрические
функции, что и в
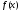 ;
; -
число корней характеристического
уравнения, совпадающих с
-
число корней характеристического
уравнения, совпадающих с
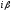 .
.
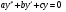 ЛОДУ
ЛОДУ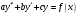 ЛОДУ
ЛОДУ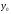 -общее
решение
-общее
решение
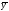 -
частное решение
-
частное решение
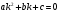 и найти его
корни;
и найти его
корни;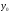
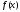 ;
; общий вид
общий вид
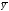 (см. табл. 3) с неизвестными коэффициентами;
(см. табл. 3) с неизвестными коэффициентами;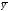 методом неопределенных коэффициентов
;
методом неопределенных коэффициентов
;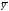 .
.
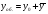 -
-