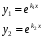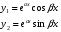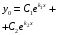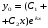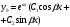- •§6 Линейные дифференциальные уравнения второго порядка
- •6.1. Общие понятия
- •§6. Линейные однородные уравнения с постоянными коэффициентами.
- •Примеры для самостоятельной работы.
- •§7 Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- •7.1.Метод вариации произвольных постоянных (метод Лагранжа) решения лнду.
- •7.2. Метод подбора частного решения лнду по виду правой части (метод неопределенных коэффициентов).
- •7.3. Структура частного решения лнду с аддитивной правой частью.
§6 Линейные дифференциальные уравнения второго порядка
-
-
6.1. Общие понятия
Определение 1: Дифференциальное уравнение 2-ого порядка вида
 ,
(1)
,
(1)
где
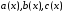 и
и
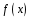
 данные
на
данные
на
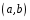 функции называется линейным ДУ
2-ого порядка (ЛНДУ).
функции называется линейным ДУ
2-ого порядка (ЛНДУ).
Определение 2: Линейное ДУ 2-ого порядка
 , (2)
, (2)
где
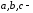 данные
действительные постоянные числа,
а
данные
действительные постоянные числа,
а
 известная
непрерывная на интервале
известная
непрерывная на интервале
 функция, называется линейным
ДУ
с постоянными
коэффициентами.
функция, называется линейным
ДУ
с постоянными
коэффициентами.
Определение
3: Если в
ДУ
(2)
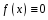 на
на
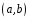 ,
то уравнение
,
то уравнение
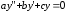 (3)
(3)
называется линейным однородным дифференциальным уравнением с постоянным коэффициентами.
. Однородное линейное ДУ(3), левая часть которого
такая же, как в неоднородном линейном ДУ(2),
называется соответствующим ему однородным
уравнением.
Определение
4:функции
называются линейно независимыми на
интервале I
,если
 .в
противном случае функции
.в
противном случае функции
 линейно
независимые.
линейно
независимые.
Определение 5: Совокупность двух линейно независимых решений ДУ называется фундаментальной системой решений данного уравнения.
Теорема 6.1.(о структуре общего решения ЛОДУ):
Пусть
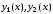 -фундаментальная
система решений ДУ,
тогда общее решение этого уравнения
имеет вид
-фундаментальная
система решений ДУ,
тогда общее решение этого уравнения
имеет вид
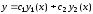
где С1,С2– произвольные постоянные.
Рассмотрим линейное неоднородное дифференциальное уравнение ЛНДУ с постоянными коэффициентами (2). Имеет место теорема о структуре его общего решения:
Теорема 6.2. (о структуре общего решения ЛНДУ):
Общее решение y
ЛНДУ
(2) есть сумма общего решения y0
соответствующего однородного уравнения
ЛОДУ
и любого частного решения
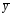 неоднородного уравнения:
неоднородного уравнения:
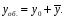
Таким образом, чтобы найти общее решение ЛНДУ, нужно найти общее решение соответствующего ЛОДУ и какое-нибудь частное решение ЛНДУ. В общем случае задача отыскания частного решения является сложной.
Частное решение ЛНДУ можно найти методом вариации произвольных постоянных или методом подбора (метод неопределенных коэффициентов).
§6. Линейные однородные уравнения с постоянными коэффициентами.
ДУ вида
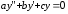 ( 3)
( 3)
называется линейным однородным дифференциальным уравнением с постоянным коэффициентами.
Где a,b,c-постоянные вещественные числа.
Будем искать
частные решения ДУ
(3) в виде
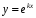 ,
где
,
где
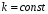 ,
тогда
,
тогда
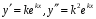 .
.
Подставляя значения
 в ДУ
(3), находим
в ДУ
(3), находим
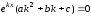
Так как
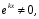 то
получим следующее алгебраическое
выражение
то
получим следующее алгебраическое
выражение
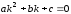 (4)
(4)
которое называется характеристическим уравнением для ЛОДУ (3).
Уравнение (4)
является уравнением 2-ой степени и имеет
2 корня
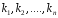 (действительных или комплексных, среди
них могут быть и равные).
(действительных или комплексных, среди
них могут быть и равные).
Каждому корню
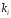 характеристического уравнения
соответствует частное решение
характеристического уравнения
соответствует частное решение
 ,
вид которого зависит от характера
корня.
,
вид которого зависит от характера
корня.
Совокупность
частных линейно независимых решений
 составляет
фундаментальную
систему решений ЛОДУ
(3).
составляет
фундаментальную
систему решений ЛОДУ
(3).
Тогда общее решение ЛОДУ (12) имеет вид:

Определение 7: Компоненты общего решения дифференциального уравнения (3) определяются в зависимости от характера корней характеристического уравнения (4) следующим образом:
1) каждому
действительному простому (т.е. не
кратному) корню
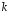 в общем решении соответствует слагаемое
вида
в общем решении соответствует слагаемое
вида
 ;
;
2) каждому
действительному корню кратности
 в общем решении соответствует слагаемое
вида
в общем решении соответствует слагаемое
вида
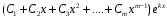 ;
;
3) каждой паре
комплексных сопряженных простых корней
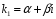 и
и
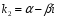 в
общем решении соответствует слагаемое
вида
в
общем решении соответствует слагаемое
вида
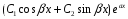 ;
;
-
каждой паре комплексных сопряженных корней
 и
и
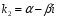 кратности
кратности
 в общем решении соответствует слагаемое
вида
в общем решении соответствует слагаемое
вида
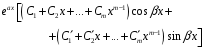 .
(16)
.
(16)
Рассмотрим частные случаи линейных однородных уравнений ЛОДУ:
а) если
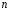 =2,
т.е. ЛОДУ
второго порядка;
=2,
т.е. ЛОДУ
второго порядка;
Способ решения ЛОДУ второго порядка состоит в том, что:
-
при помощи замены
 -
через
-
через
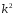 ,
,
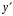 -
через
-
через
 ,
,
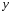 -
через 1
-
через 1
составляется характеристическое уравнение, соответствующее данному ЛОДУ;
-
решается характеристическое уравнение, находятся корни:
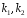
-
устанавливается характер корней (действительные или комплексные, различные или кратные) и определяется соответствующая этим корням фундаментальная система решений
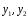
-
составляется общее решение ЛОДУ:
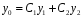 .
.
Последовательность нахождения общего решения ЛОДУ второго порядка и приемы составления фундаментальной системы решений представлены в таблице 2 .
Таблица 2.
Общее решение (ЛОДУ) второго порядка.
|
Порядок |
n=2 |
||
|
Общий вид ЛОДУ |
|
||
|
Характеристическое уравнение |
|
||
|
Характер корней |
|
|
|
|
Фундаментальная система решений |
|
|
|
|
Общее решение |
|
|
|
Пример1. Найти фундаментальную систему решений ДУ:

Решение.
-
характеристическое уравнение:
 ;
;
-
корни
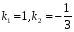 ;
; -
так как корни действительные различные, то фундаментальная система решений:
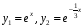 .
.

Ответ:
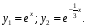
Пример 2. Найти фундаментальную систему решений ДУ:
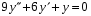 .
.
Решение.
-
Характеристическое уравнение:
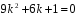 ;
; -
корни:
 ;
; -
так как
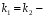 действительные числа, то фундаментальная
система решений:
действительные числа, то фундаментальная
система решений:
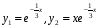 .
.
Ответ:
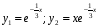 .
.
Пример 3. Найти фундаментальную систему решений и общее решение ДУ:
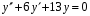 .
.
Решение.
-
Характеристическое уравнение:
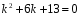 ;
; -
корни:
 ;
; -
так как корни комплексно сопряженные, то фундаментальная система решений:
 ;
; -
общее решение
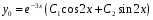 .
.
Ответ:
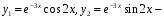 фундаментальная система решений;
фундаментальная система решений;
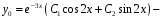 общее решение.
общее решение.
Пример4. Найти фундаментальную систему решений и общее решение ДУ:
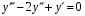
Решение.
-
Характеристическое уравнение:
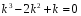 ;
; -
корни:
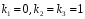 ;
; -
так как все корни – действительные числа и два из них одинаковы, то фундаментальная система решений
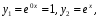
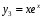 ;
;
-
общее решение
 .
.
Ответ:
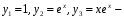 фундаментальная система решений;
фундаментальная система решений;
 общее решение.
общее решение.

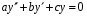
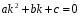
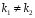 -
действительные различные числа
-
действительные различные числа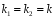
 действительные одинаковые числа
действительные одинаковые числа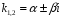 -
комплексно сопряженные числа
-
комплексно сопряженные числа