
- •§6 Линейные дифференциальные уравнения второго порядка
- •6.1. Общие понятия
- •§6. Линейные однородные уравнения с постоянными коэффициентами.
- •Примеры для самостоятельной работы.
- •§7 Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
- •7.1.Метод вариации произвольных постоянных (метод Лагранжа) решения лнду.
- •7.2. Метод подбора частного решения лнду по виду правой части (метод неопределенных коэффициентов).
- •7.3. Структура частного решения лнду с аддитивной правой частью.
Примеры для самостоятельной работы.
Найти фундаментальную систему решений дифференциального уравнения:
6.1.
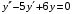 .
.
6.2. .
.
6.3.
 .
.
6.4.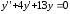 .
.
6.5.
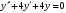 .
.
6.6.
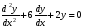 .
.
Найти общее решение дифференциального уравнения:
6.7.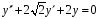 .
.
6.8.
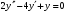 .
.
6.9.
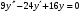 .
.
6.10.
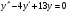 .
.
6.11.
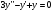
6.12.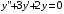 .
.
6.13
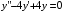
6.14.
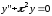 .
.
6.15.
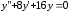 .
.
6.16.
 .
.
6.17.
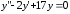 .
.
6.18.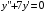 .
.
6.19.
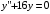 .
.
6.20
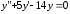
Решить задачи Коши или краевые задачи:
6.21.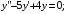
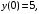
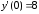 .
.
6.22.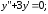

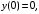
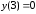 .
.
6.23.
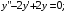
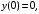
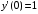 .
.
6.24.
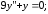
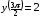 ,
,
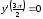 .
.
6.25.
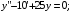
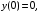
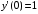 .
.
Ответы:
6.1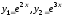
6.2.
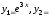

6.3
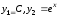
6.4.
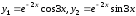
6.5.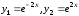
6.6.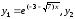
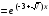
6.7.
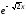
6.8.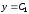

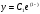
6.9.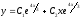
6.10.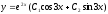
6.11.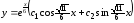 .
.
6.12.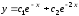 .
.
6.13.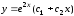
6.14.
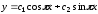 .
.
6.15.
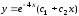 .
.
6.16.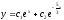
6.17.
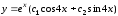 .
.
6.18.
 .
.
6.19.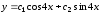 .
.
6.20.
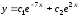
6.21.
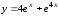 .
.
6.22..
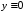 .
.
6.23..
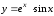 .
.
6.24.
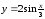 .
.
6.25..
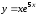 .
.
§7 Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.
Рассмотрим случай линейного неоднородного дифференциального уравнения с постоянными коэффициентами ЛНДУ
 (2),
(2),
где a,
b,
c
- действительные
постоянные, а

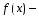 непрерывная на некотором интервале
функция.
непрерывная на некотором интервале
функция.
Теорема 7.2. (о структуре общего решения ЛНДУ):
Общее решение y
ЛНДУ
(2) есть сумма общего решения y0
соответствующего однородного уравнения
ЛОДУ
и любого частного решения
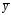 неоднородного уравнения:
неоднородного уравнения:
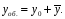
Таким образом, чтобы найти общее решение ЛНДУ, нужно найти общее решение соответствующего ЛОДУ и какое-нибудь частное решение ЛНДУ. В общем случае задача отыскания частного решения является сложной.
Частное решение ЛНДУ можно найти методом вариации произвольных постоянных или методом подбора (метод неопределенных коэффициентов
по виду правой части уравнении.)
7.1.Метод вариации произвольных постоянных (метод Лагранжа) решения лнду.
Сущность этого
метода решения ЛНДУ
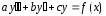 состоит в следующем.
состоит в следующем.
-
Сначала находится общее решение соответствующего ЛОДУ:
-
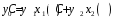 ,
,
где
 и
и
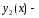 линейно независимые решения ЛОДУ.
линейно независимые решения ЛОДУ.
-
Полагают, что
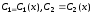 ,
и общее решение
,
и общее решение
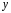 ЛНДУ
ищутся в том же виде, что и
ЛНДУ
ищутся в том же виде, что и
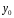 ,
т.е.
,
т.е.
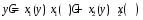 .
.
-
Составляется и решается следующая система уравнений:
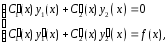 (1)
(1)
которая имеет
единственное решение
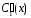 и
и
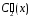 ,
так как определитель этой системы
,
так как определитель этой системы
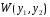 не равен нулю (поскольку
не равен нулю (поскольку
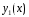 и
и
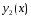 - линейно независимые).
- линейно независимые).
Решение системы (1) находится по формулам
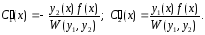
Определитель
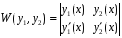 - называется определителем
Вронского для функций
- называется определителем
Вронского для функций
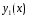 и
и
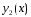 .
.
-
Интегрируя найденные
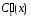 и
и
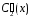 по
по
 находятся
находятся
 .
.
-
Подставляются найденные
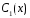 и
и
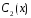 в
в
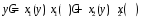 и записывается общее решение ЛНДУ.
и записывается общее решение ЛНДУ.
Пример1. Найти общее решение дифференциального уравнения:
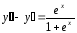 .
.
Решение.
-
Находим общее решение ЛОДУ:
 .
Характеристическое уравнение
.
Характеристическое уравнение
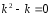 .
Его корни
.
Его корни
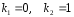 .
.
Общее решение
ЛОДУ
:
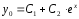 .
.
-
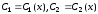 .
.
-
Общее решение ЛНДУ ищем в виде
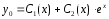 .
. 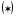
-
Составим и решим систему уравнений вида (18)
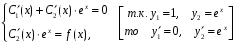 .
.
-
Найдем
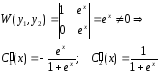 .
.
-
Интегрируя
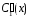 и
и
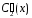 ,
находим
,
находим
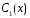 и
и
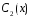 :
:
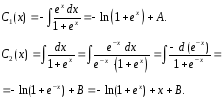
-
Подставим
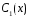 и
и
 в
в
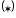 ,
найдем решение ЛНДУ:
,
найдем решение ЛНДУ:
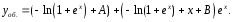
Ответ:
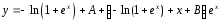 .
.
Пример 2. Найти частное решение дифференциального уравнения
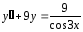 ,
если
,
если
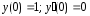 .
.
Решение.
-
Находим общее решение соответствующего линейного однородного дифференциального уравнения:
 .
.
Характеристическое
уравнение
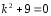 .
Его корни
.
Его корни
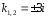 ,
следовательно, общее решение линейного
однородного дифференциального уравнения:
,
следовательно, общее решение линейного
однородного дифференциального уравнения:
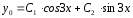 .
.
-
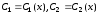 .
. -
Общее решение линейного неоднородного дифференциального уравнения ищем в виде
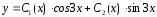
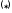
-
Составим и решим систему уравнений вида (18):
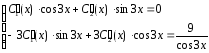 ,
,
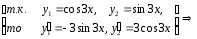
 .
.
Найдём
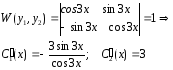 .
.
-
Интегрируя
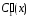 и
и
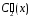 ,
находим
,
находим
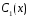 и
и
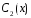 :
:
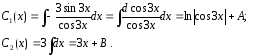
-
Подставляются найденные
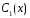 и
и
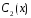 в
в
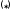 и записывается общее решение ЛНДУ.
и записывается общее решение ЛНДУ.
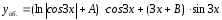 .
.
-
Найдём частное решение данного дифференциального уравнения. Для этого определим А и В, используя начальные условия:
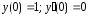 .
.
-
Найдём сначала
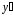 (дифференцированием найденного общего
решения
(дифференцированием найденного общего
решения
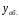 ).
).
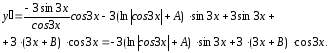
Подставив
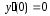 ,
получим:
,
получим:
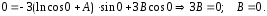
-
Подставив
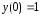 в
общее решение
в
общее решение
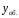 ,
получим:
,
получим:
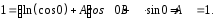
Таким образом
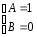 .
Поставив эти значения в общее решение,
получим частное решение
.
Поставив эти значения в общее решение,
получим частное решение
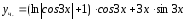 .
.
Ответ:
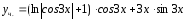 .
.
З а м е ч а н и е.
Метод
вариации произвольных постоянных
является общим и может применяться при
любых видах правой части ЛНДУ.
Вместе с тем, по некоторым видам правой
части ЛНДУ
можно подобрать
частное решение
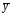 ЛНДУ
методом неопределенных коэффициентов.
ЛНДУ
методом неопределенных коэффициентов.
