Глава 11. Волны в упругой среде

11.1. Упругие волны

Процесс распространения колебаний в пространстве называется волной. Среду, в которой распространяются колебания, будем рассматривать как сплошную и непрерывную, отвлекаясь от ее атомистического строения. При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Упругой волной называют процесс распространения возмущения в упругой среде. Различают волны продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлению распространения волны.

Продольные волны могут распространяться в средах, в которых возникают упругие силы при деформации сжатия и растяжения (в твердых, жидких и газообразных телах). Поперечные волны могут распространяться в среде, в которой возникают упругие силы при деформации сдвига (фактически только в твердых телах).

Рис. 11.1. Гармоническая поперечная волна

Упругая волна называется гармонической, если колебания частиц среды являются гармоническими. На рис. 11.1 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси x. Приведенный график отличается от графика гармонического колебания тем, что он дает зависимость смещения частиц среды ξ от расстояния x до источника колебаний в данный момент времени, а график колебаний – зависимость смещения данной частицы от времени.

Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны λ. Длина волны равна расстоянию, на которое распространяется фаза колебания за период:

.

Учитывая, что , где – частота колебаний, получаем

.

Волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени – один. Волновой фронт также является волновой поверхностью. Волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется плоской или сферической.

11.2. Уравнение плоской и сферической волн

Уравнением волны называется выражение, которое даст смещение ξ колеблющейся точки, как функцию ее координат х, у, z и времени t:

.

Найдем вид функции ξ в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось х совпала с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны к оси x. Все точки волновой поверхности колеблются одинаково, поэтому смещение будет зависеть только от х и t:

.

Пусть колебания точек, лежащих в плоскости x=0, имеют вид

.

Найдем вид колебания частиц в плоскости, соответствующей произвольному значению х.

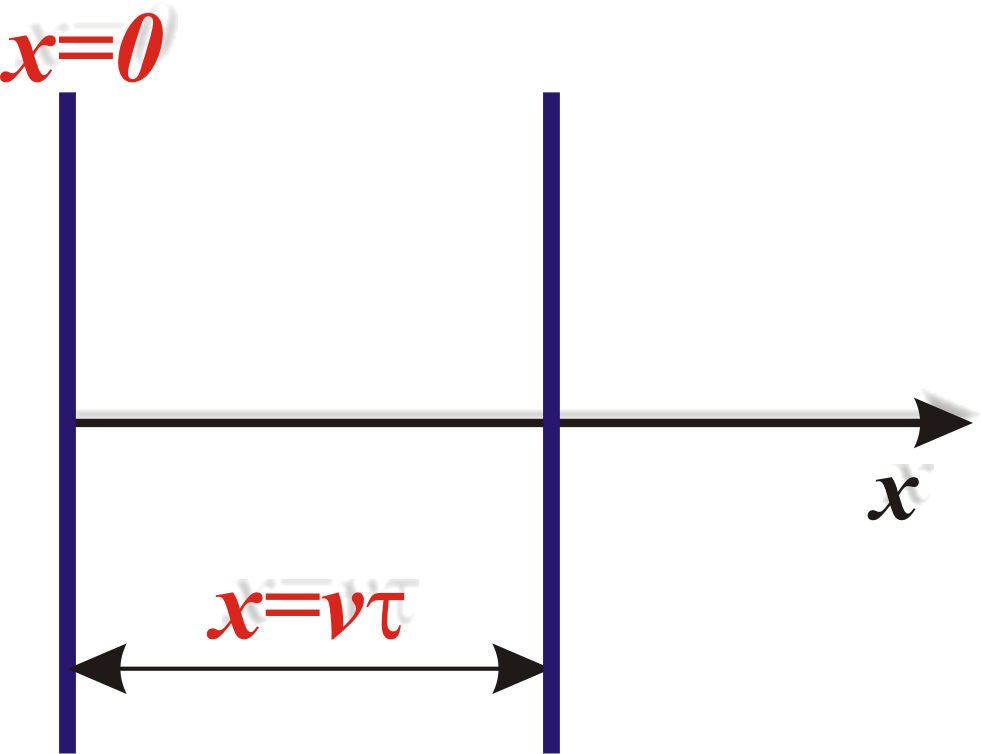
Рис. 11.2. Распространение плоской волны

Чтобы пройти путь от плоскости x=0 до данной плоскости требуется время:

,

где – v скорость распространения волны. Колебания частиц, лежащих в плоскости x, будут отставать по времени на τ от колебаний частиц в плоскости х=0 и будут иметь вид:

. (11.1)

Величина ξ представляет собой смещение любой из точек с координатой x в момент времени t.

Зафиксируем значение фазы:

.

Продифференцировав последнее выражение по времени, можем найти скорость, с которой перемещается фаза волны:

, , (11.2)

т.е. скорость распространения волны есть скорость перемещения фазы, поэтому ее называют фазовой скоростью. Уравнения (11.1) и (11.2) описывают волну, распространяющуюся в сторону возрастания х. Волна, распространяющаяся в противоположном направлении, описывается уравнениями

, .

Введем волновое число k:

.

Волновое число связано с циклической частотой и фазовой скоростью соотношением:

.

Подставим в (11.1):

.

Найдем уравнение сферической волны. Будем считать источник точечным. Если скорость распространения волны во всех направления одинакова, то порождаемая точечным источником волна будет сферической. Рассмотрим фазу колебаний источника, равную . Точки, лежащие на волновой поверхности радиуса r, будут колебаться с фазой . Амплитуда колебаний в этом случае даже если энергия волны не поглощается средой, убывает с расстоянием от источника по закону . Следовательно, уравнение сферической волны имеет вид:

,

где а – постоянная величина, численно равная амплитуде на расстоянии от источника, равном единице.